Lineare zeitinvariante Systeme/Laplace–Transformation und p–Übertragungsfunktion

1. Lineare zeitinvariante Systeme
2. Beschreibung kausaler realisierbarer Systeme
3. Laplace–Transformation und p–Übertragungsfunktion

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

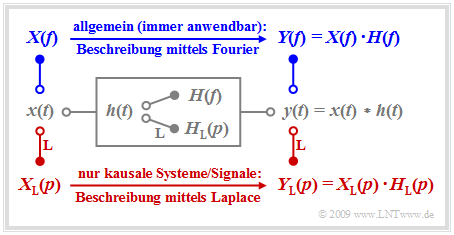
Betrachtetes Systemmodell

Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort $h(t)$, an dessen Eingang das Signal $x(t)$ anliegt. Das Ausgangssignal $y(t)$ ergibt sich dann als das Faltungsprodukt $x(t) ∗ h(t)$.

Allgemeines (auch akausales) sowie kausales Systemmodell

Bei akausalen Systemen und Signalen muss zur Beschreibung des Spektralverhaltens stets das erste Fourierintegral angewendet werden, und es gilt für das Ausgangsspektrum:

$$Y(f) = X(f) \cdot H(f) \hspace{0.05cm}.$$

Das Fourierintegral besitzt auch für kausale Systeme und Signale, also unter der Voraussetzung

$$x(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0\hspace{0.05cm},\hspace{0.2cm} h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} y(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}$$

weiterhin Gültigkeit. In diesem Fall ergeben sich aber durch Anwendung der Laplace–Transformation unter Beachtung gewisser Restriktionen wesentliche Vorteile:

• Die so behandelten Systeme sind stets durch eine Schaltung realisierbar. Der Entwickler kommt nicht in Versuchung, realitätsfremde Lösungen anzubieten.
• Die Laplace–Transformierte $X_{\rm L}(p)$ ist stets eine reelle Funktion der Spektralvariablen $p$. Dass sich diese Variable entsprechend $p = {\rm j} · 2πf$ aus der Multiplikation der physikalischen Kreisfrequenz $ω = 2πf$ mit der imaginären Einheit $\rm j$ ergibt, spielt für den Anwender keine Rolle.
• Die implizite Bedingung $x(t) = 0$ für $t < 0$ erlaubt speziell die Analyse des Einschwingverhaltens nach Einschaltvorgängen in einfacherer Weise als mit dem Fourierintegral.

Definition der Laplace–Transformation

Ausgehend vom ersten Fourierintegral,

$$X(f) = \int_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t,$$

ergibt sich bei kausaler Zeitfunktion (⇒   $x(t) = 0$ für $t < 0$) mit der formalen Substitution $p = {\rm j} · 2πf$ direkt die Laplace–Transformation.

$\text{Definition:}$  Die Laplace–Transformierte einer kausalen Zeitfunktion $x(t)$ lautet:

$$X_{\rm L}(p) = \int_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t} }\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}.$$

Der Zusammenhang zwischen der Laplace–Transformierten $X_{\rm L}(p)$ und dem physikalischen Spektrum $X(f)$ ist häufig wie folgt gegeben:

$$X(f) = X_{\rm L}(p) \Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}={\rm \hspace{0.05cm} j\hspace{0.05cm}2\pi \it f}}}.$$

Hat allerdings das Signal $x(t)$ periodische Anteile und beinhaltet damit die Spektralfunktion $X(f)$ zusätzliche Diracfunktionen, so ist diese Gleichung nicht anwendbar. In diesem Fall muss $p = α + {\rm j} · 2πf$ angesetzt werden und es ist dann der Grenzübergang $α → 0$ zu bilden.

$\text{Beispiel 1:}$  Wir gehen von der einseitig exponentiell abfallenden Zeitfunktion entsprechend der Skizze im Beispiel 1 des Kapitels „Real– und Imaginärteil einer kausalen Übertragungsfunktion” aus:

$$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$

Damit lautet die Laplace–Transformierte:

$$X_{\rm L}(p) = \int_{0}^{\infty} {\rm e}^{-t/T} \cdot {\rm e}^{-pt} \hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.05cm}\cdot \hspace{0.05cm}t}}\hspace{0.05cm}\Bigg \vert_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$

Mit $p = {\rm j} · 2πf$ erhält man die herkömmliche Spektralfunktion bezüglich $f$:

$$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$

Betrachtet man dagegen den Frequenzgang eines Tiefpasses erster Ordnung, dessen Impulsantwort $h(t)$ sich gegenüber der obigen Zeitfunktion um den Faktor $1/T$ unterscheidet, so gilt für die Laplace–Transformierte bzw. die Fourier–Transformierte:

$$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.8cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT} } = \frac {1}{1+{\rm j} \cdot f/f_{\rm G} } \hspace{0.05cm} .$$

Häufig verwendet man dann anstelle des Parameters $T$ die 3dB–Grenzfrequenz $f_{\rm G} = 1/(2πT)$.

Einige wichtige Laplace–Korrespondenzen

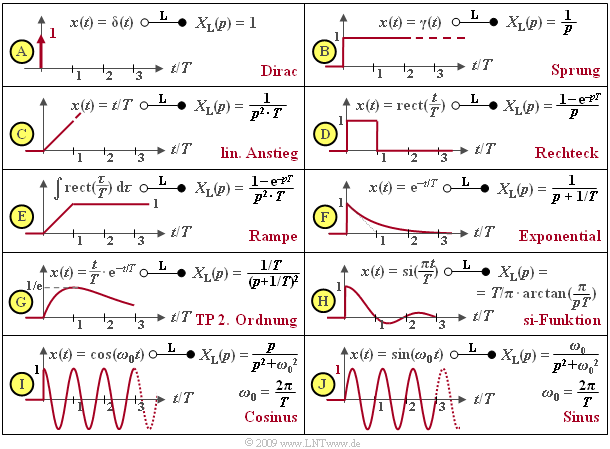
Nachfolgend sind einige wichtige Laplace–Korrespondenzen zusammengestellt. Alle hier betrachteten Zeitsignale $x(t)$ sind als dimensionslos angenommen. Aus diesem Grund besitzt $X_{\rm L}(p)$ dann als Integral über die Zeit stets die Einheit „Sekunde”.

Tabelle mit einigen Laplace-Transformierten

Die Laplace–Transformierte der Diracfunktion $δ(t)$ ist $X_{\rm L}(p) = 1$ (Diagramm $\rm A$). Durch Anwendung des Integrationssatzes erhält man $X_{\rm L}(p) = 1/p$ für die Sprungfunktion $γ(t)$ (Diagramm $\rm B$) und aus dieser durch Multiplikation mit $1/(pT)$ die Laplace–Transformierte der linear ansteigenden Funktion $x(t) = t/T$ für $t > 0$ (Diagramm $\rm C$).

Die Rechteckfunktion kann aus der Subtraktion zweier um $T$ auseinanderliegender Sprungfunktionen $γ(t)$ und $γ(t – T)$ erzeugt werden, so dass sich nach dem Verschiebungssatz die Laplace–Transformierte $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$ ergibt (Diagramm $\rm D$). Durch Integration erhält man daraus die Rampenfunktion bzw. nach Multiplikation mit $1/(pT)$ deren Laplace–Transformierte (Diagramm $\rm E$).

Die Exponentialfunktion (Diagramm $\rm F$) wurde bereits auf der letzten Seite betrachtet. Mit dem Faktor $1/T$ beschreibt diese gleichzeitig die Impulsantwort eines Tiefpasses erster Ordnung. Durch Quadrierung erhält man die $p$–Spektralfunktion eines Tiefpasses zweiter Ordnung. Die zugehörige Zeitfunktion lautet $x(t) = t/T · {\rm e}^{–t/T}$ (Diagramm $\rm G$).

Neben der kausalen $\rm si$–Funktion (Diagramm $\rm H$) sind in der Tabelle auch die Laplace–Transformierten der kausalen Cosinus– und Sinusfunktion (Diagramme $\rm I$ und $\rm J$) angegeben, die sich zu $p/(p^2 + ω_0^2)$ bzw. $ω_0/(p^2 + ω_0^2)$ ergeben. Hierbei bezeichnet $ω_0 = 2πf_0 = 2π/T$ die so genannte Kreisfrequenz.

Pol–Nullstellen–Darstellung von Schaltungen

Ein jedes lineare zeitinvariante System (LZI), das durch eine Schaltung aus diskreten zeitkonstanten Bauelementen wie

• Widerständen $(R)$,
• Kapazitäten $(C)$,
• Induktivitäten $(L)$ und
• Verstärkerelementen

realisiert werden kann, besitzt eine gebrochen–rationale $p$–Übertragungsfunktion:

$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{...} + A_2 \cdot p^2 + A_1 \cdot p + A_0} {B_N \cdot p^N +\text{...} + B_2 \cdot p^2 + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$

Alle Koeffizienten des Zählers  ⇒  $A_Z, \text{...} , A_0$ und des Nenners  ⇒  $B_N, \text{...} , B_0$ sind reell. Weiter bezeichnen

• $Z$ den Grad des Zählerpolynoms $Z(p)$,
• $N$ den Grad des Nennerpolynoms $N(p)$.

$\text{Äquivalente Pol–Nullstellen–Darstellung:}$   Für die $p$–Übertragungsfunktion kann auch geschieben werden:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i} } {\prod\limits_{i=1}^N p - p_{\rm x i} }= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

Die $Z + N + 1$ Parameter bedeuten:

• $K = A_Z/B_N$ ist ein konstanter Faktor. Gilt $Z = N$, so ist dieser dimensionslos.
• Die Lösungen der Gleichung $Z(p) = 0$ ergeben die $Z$ Nullstellen $p_{o1},\text{...}, p_{oZ}$ von $H_{\rm L}(p)$.
• Die Nullstellen des Nennerpolynoms $N(p)$ liefern die $N$ Polstellen (oder kurz Pole).

Die Umformung ist eindeutig. Dies erkennt man daran, dass die $p$–Übertragungsfunktion gemäß der ersten Gleichung ebenfalls nur durch $Z + N + 1$ freie Parameter bestimmt ist, da einer der Koeffizienten $A_Z, \text{...} , A_0, B_N, \text{...} , B_0$ ohne Änderung des Quotienten auf $1$ normiert werden kann.

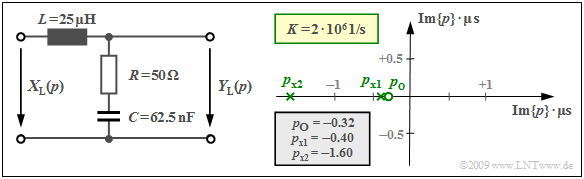
$\text{Beispiel 2:}$  Wir betrachten den gezeichneten Vierpol mit einer Induktivität $L$ (komplexer Widerstand $pL$) im Längszweig sowie im Querzweig die Serienschaltung eines Ohmschen Widerstandes $R$ und einer Kapazität $C$ mit dem komplexen Widerstand $1/(pC)$.

Betrachteter Vierpol und dazugehöriges Pol–Nullstellen–Diagramm

Damit lautet die $p$–Übertragungsfunktion:

$$H_{\rm L}(p)= \frac {Y_{\rm L}(p)} {X_{\rm L}(p)}= \frac {R + {1}/{(pC)} } {pL + R +{1}/{(pC)} }= \frac {1 + p \cdot{RC} } {1 + p \cdot{RC}+ p^2 \cdot{LC} } \hspace{0.05cm} .$$

Setzt man $p = {\rm j} · 2πf$ ein, so erhält man die Fourier–Übertragungsfunktion (bzw. den Frequenzgang). Dividiert man in obiger Gleichung Zähler und Nenner durch $LC$, so ergibt sich:

$$H_{\rm L}(p)= \frac {R} {L}\cdot \frac {p + {1}/{(RC)} } {p^2 + {R}/ {L}\cdot p + {1}/{(LC)} }= K \cdot \frac {p - p_{\rm o } } {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$

Im rechten Gleichungsteil ist die Übertragungsfunktion $H_{\rm L}(p)$ in Pol–Nullstellen–Notation angegeben. Durch Koeffizientenvergleich ergeben sich für $R = 50 \ \rm Ω$, $L = 25\ \rm µ H$ und $C = 62.5 \ \rm nF$ folgende Werte:

• die Konstante $K = R/L = 2 · 10^6 \cdot 1/{\rm s}$,
• die Nullstelle $p_o = –1/(RC) = –0.32 · 10^6 \cdot 1/{\rm s},$
• die beiden Pole $p_{x1}$ und $p_{x2}$ als Lösung der Gleichung

$$p^2 + \frac {R} {L}\cdot p + \frac{1}{LC} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -\frac {R} {2L}\pm \sqrt{\frac {R^2} {4L^2}- \frac{1}{LC} }$$

$$\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -10^6 \cdot {1}/{\rm s} \pm \sqrt{10^{12} \cdot {1} /{\rm s^2}-0.64 \cdot 10^{12} \cdot {1}/ {\rm s^2} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm x 1 }= -0.4 \cdot 10^6\cdot {1}/ {\rm s},\hspace{0.2cm}p_{\rm x 2 }= -1.6 \cdot 10^6\cdot {1}/ {\rm s} \hspace{0.05cm} .$$

In der obigen Grafik ist rechts das Pol–Nullstellen–Diagramm angegeben.

• Die beiden Achsen bezeichnen den Real– und den Imaginärteil der Variablen $p$, jeweils normiert auf den Wert $10^6 · \rm 1/s\; (= 1/µs)$.
• Man erkennt nach dieser Normierung die Nullstelle bei $p_{\rm o} =\, –0.32$ als Kreis und die Polstellen bei $p_{\rm x1} = \,–0.4$ und $p_{\rm x2} = \,–1.6$ als Kreuze.

Eigenschaften der Pole und Nullstellen

Die Übertragungsfunktion $H_{\rm L}(p)$ einer jeden realisierbaren Schaltung wird durch $Z$ Nullstellen und $N$ Pole zusammen mit einer Konstanten $K$ vollständig beschrieben, wobei folgende Einschränkungen gelten:

• Es gilt stets $Z ≤ N$. Mit $Z > N$ wäre im Grenzfall für $p → ∞$ (also für sehr hohe Frequenzen) auch die $p$–Übertragungsfunktion „unendlich groß”.
• Die Nullstellen $p_{\rm oi}$ und die Pole $p_{\rm xi}$ sind im allgemeinen komplex und weisen wie $p$ die Einheit $\rm 1/s$ auf. Gilt $Z < N$, so besitzt auch die Konstante $K$ eine Einheit.
• Die Pole und Nullstellen können reell sein, wie im letzten Beispiel gezeigt. Sind sie komplex, so treten immer zwei konjugiert–komplexe Polstellen bzw. zwei konjugiert–komplexe Nullstellen auf, da $H_{\rm L}(p)$ stets eine reelle gebrochen–rationale Funktion darstellt.
• Alle Pole liegen in der linken Halbebene oder – als Grenzfall – auf der imaginären Achse. Diese Eigenschaft ergibt sich aus der erforderlichen und vorausgesetzten Kausalität zusammen mit dem Hauptsatz der Funktionstheorie, der im nächsten Kapitel angegeben wird.
• Nullstellen können sowohl in der linken als auch in der rechten $p$–Halbebene auftreten oder auch auf der imaginären Achse. Ein Beispiel für Nullstellen in der rechten Halbebene findet man in der Aufgabe 3.4Z, die sich mit Allpässen beschäftigt.
• Bei den so genannten Minimum–Phasen–Systemen sind in der rechten $p$–Halbebene nicht nur Pole verboten, sondern auch Nullstellen. Der Realteil aller Singularitäten ist hier nie positiv.

Diese Eigenschaften werden nun an drei Beispielen verdeutlicht.

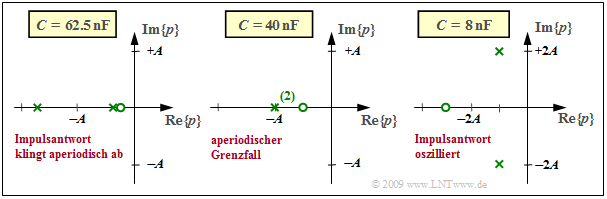
$\text{Beispiel 3:}$  Ausgehend von der bereits im letzten Abschnitt betrachteten Vierpolschaltung $(L$ im Längszweig, $R$ und $C$ im Querzweig) können die charakteristischen Größen der Übertragungsfunktion wie folgt angegeben werden:

$$K = 2A, \hspace{0.2cm}p_{\rm x 1,\hspace{0.05cm}2 }= -A \pm \sqrt{A^2-B^2}, \hspace{0.2cm}p_{\rm o }= - \frac{B^2}{2A} \hspace{0.05cm} \hspace{0.2cm} {\rm mit } \hspace{0.2cm} A = \frac {R} {2L}, \hspace{0.2cm}B = \frac{1}{\sqrt{LC} } \hspace{0.05cm}.$$

Die Grafik zeigt drei verschiedene Diagramme mit unterschiedlichen Kapazitätswerten $C$. Es gilt stets $R = 50 \ \rm Ω$ und $L = 25 \ \rm µ H$. Die Achsen sind auf die Variable $A = R/(2L) = 10^6 · \rm 1/s$ normiert, und der konstante Faktor ist jeweils $K = 2A = 2 · 10^6 · \rm 1/s.$

Lage der Nullstelle und der Pole für Z = 1 und N = 2

• Für $B < A$ erhält man zwei reelle Pole und eine Nullstelle rechts von $–A/2$. Für $C = 62.5 \ \rm nF$ ergibt sich gemäß dem linken Diagramm:

$$ {B}/ {A}= 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A = -0.4 , \hspace{0.2cm}p_{\rm x 2}/A= -1.6 , \hspace{0.2cm}p_{\rm o}/A= -0.32 \hspace{0.05cm} .$$

• Für $B > A$ ergeben sich zwei konjugiert–komplexe Pole und eine Nullstelle links von $–A/2$, wie im rechten Diagramm für $C = 8 \ \rm nF$:

$${B}/ {A}= \sqrt{5} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }/A= -1\pm {\rm j}\cdot 2,\hspace{0.2cm}p_{\rm o}/A\approx -2.5 \hspace{0.05cm} .$$

• Der Grenzfall $A = B$ führt zu einer reellen doppelten Polstelle und einer Nullstelle bei $– A/2$ (mittleres Diagramm, gültig für $C = 400 \ \rm nF$):

$$ {B}/ {A}= 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A= p_{\rm x 2}/A= -1, \hspace{0.2cm}p_{\rm o}/A= -0.5 \hspace{0.05cm} .$$

Die Impulsantworten $h(t)$ ergeben sich entsprechend dem folgenden Kapitel Laplace–Rücktransformation wie folgt:

• Bei der linken Konstellation ist $h(t)$ aperiodisch abklingend.
• Bei der rechten Konstellation ist $h(t)$ gedämpft oszillierend.
• Bei der mittleren Konstellation spricht man vom aperiodischen Grenzfall.

Grafische Ermittlung von Dämpfung und Phase

Gegeben sei die $p$–Übertragungsfunktion in der Pol–Nullstellen–Notation:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z (p - p_{\rm o i})} {\prod\limits_{i=1}^N (p - p_{\rm x i})}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

Zur herkömmlichen Übertragungsfunktion bzw. zum Frequenzgang $H(f)$ kommt man, indem man das Argument $p$ von $H_{\rm L}(p)$ durch ${\rm j} \cdot 2πf$ ersetzt:

$$H(f)= K \cdot \frac {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 2})\cdot \text{...} \cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} \hspace{-0.03cm} Z})} {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 2})\cdot \text{...}\cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

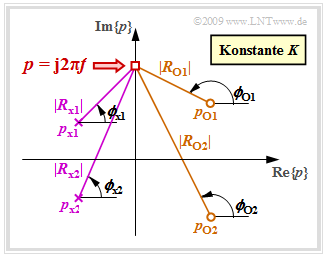
Wir betrachten nun eine feste Frequenz $f$ und beschreiben die Abstände und Winkel aller Nullstellen durch Vektoren:

Ausgangsdiagramm zur Berechnung von Dämpfung und Phase

$$R_{ {\rm o} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} i}= |R_{{\rm o} i}| \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm}\cdot\hspace{0.03cm}\phi_{ {\rm o} i} }, \hspace{0.3cm}i= 1, \text{...}\ , Z \hspace{0.05cm} .$$

In gleicher Weise gehen wir für die Polstellen vor:

$$R_{ {\rm x} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} i}= |R_{ {\rm x} i}| \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm}\cdot\hspace{0.03cm}\phi_{ {\rm x} i} }, \hspace{0.3cm}i= 1, \text{...}\ , N \hspace{0.05cm} .$$

Die Grafik zeigt die Beträge und Phasenwinkel für ein System

• mit $Z = 2$ Nullstellen in der rechten Halbebene
• und $N = 2$ Polstellen in der linken Halbebene.

Zu berücksichtigen ist zudem die Konstante $K$.

Mit dieser Vektordarstellung kann für den Frequenzgang geschrieben werden:

$$H(f)= K \cdot \frac {|R_{ {\rm o} 1}| \cdot |R_{ {\rm o} 2}|\cdot ... \cdot |R_{ {\rm o} \hspace{-0.03cm} Z}|} {|R_{ {\rm x} 1}| \cdot |R_{ {\rm x} 2}|\cdot \text{...} \cdot |R_{ {\rm x} \hspace{-0.03cm} N}|} \cdot {\rm e^{\hspace{0.03cm}{\rm j} \hspace{0.05cm}\cdot [ \phi_{ {\rm o} 1}\hspace{0.1cm}+ \hspace{0.1cm}\phi_{ {\rm o} 2} \hspace{0.1cm}+ \hspace{0.1cm}\hspace{0.1cm}\text{...}. \hspace{0.1cm} + \hspace{0.1cm}\phi_{ {\rm o} \hspace{-0.03cm}{\it Z}}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 1}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 2} \hspace{0.1cm}- \hspace{0.1cm}... \hspace{0.1cm} - \hspace{0.1cm} \phi_{ {\rm x} \hspace{-0.03cm}{\it N} }]} } \hspace{0.05cm} .$$

Stellt man $H(f)$ durch die Dämpfungsfunktion $a(f)$ und die Phasenfunktion $b(f)$ nach der allgemein gültigen Beziehung $H(f) = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$ dar, so erhält man durch den Vergleich mit der obigen Gleichung das folgende Ergebnis:

• Bei geeigneter Normierung aller dimensionsbehafteten Größen gilt für die Dämpfung in Neper ($1 \ \rm Np$ entspricht $8.686 \ \rm dB$):

$$a(f) = -{\rm ln} \hspace{0.1cm} K + \sum \limits_{i=1}^N {\rm ln} \hspace{0.1cm} |R_{ {\rm x} i}|- \sum \limits_{i=1}^Z {\rm ln} \hspace{0.1cm} |R_{ {\rm o} i}| \hspace{0.05cm} .$$

• Die Phasenfunktion in Radian (rad) ergibt sich entsprechend der oberen Skizze zu

$$b(f) = \phi_K + \sum \limits_{i=1}^N \phi_{ {\rm x} i}- \sum \limits_{i=1}^Z \phi_{ {\rm o} i}\hspace{0.2cm}{\rm mit} \hspace{0.2cm} \phi_K = \left\{ \begin{array}{c} 0 \\ \pi \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \end{array}\begin{array}{*{20}c} { K > 0\hspace{0.05cm},} \\ { K <0\hspace{0.05cm}.} \end{array}$$

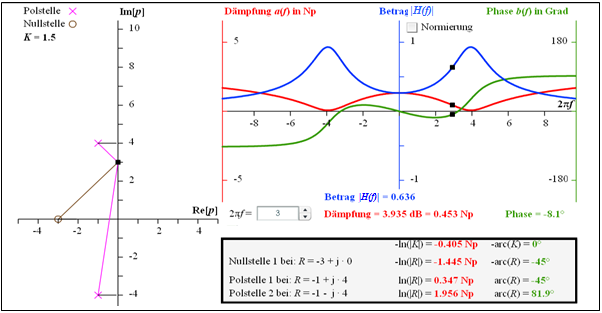
$\text{Beispiel 4:}$  Die Grafik verdeutlicht die Berechnung

• der Dämpfungsfunktion $a(f)$   ⇒   roter Kurvenverlauf, und
• der Phasenfunktion $b(f)$   ⇒   roter Kurvenverlauf

eines Vierpols, der durch den Faktor $K = 1.5$, eine Nullstelle bei $–3$ und zwei Pole bei $–1 \pm {\rm j} · 4$ festliegt. Die angegebenen Zahlenwerte gelten für die Frequenz $2πf = 3$:

$$a \left [f = {3}/({2\pi}) \right ] = 0.453\,\,{\rm Np}= 3.953\,\,{\rm dB} \hspace{0.4cm}\Rightarrow \hspace{0.4cm}\vert H \left [f = {3}/({2\pi}) \right ]\vert = 0.636, \hspace{0.4cm} b\left [f = {3}/({2\pi}) \right ] = -8.1^\circ \hspace{0.05cm} .$$

Zur Berechnung der Dämpfungs– und Phasenfunktion (Bildschirmabzug des Programms „Kausale Systeme & Laplace–Transformation” in einer früheren Version)

Die Herleitung dieser Zahlenwerte ist im umrahmten Block verdeutlicht.

Für den Betragsfrequenzgang $\vert H(f)\vert$   ⇒   blauer Kurvenverlauf ergibt sich ein bandpassähnlicher Verlauf mit

$$\vert H(f = 0)\vert \approx 0.25\hspace{0.05cm}, $$

$$\vert H(f = \frac{4}{2\pi})\vert \approx 0637\hspace{0.05cm},$$

$$\vert H(f \rightarrow \infty)\vert= 0 \hspace{0.05cm} .$$

Aufgaben zum Kapitel

Aufgabe 3.2: Laplace-Transformation

Aufgabe 3.2Z: Laplace und Fourier

Aufgabe 3.3: p-Übertragungsfunktion

Aufgabe 3.3Z: Hoch- undTiefpässe in p-Form

Aufgabe 3.4: Dämpfungs- und Phasenverlauf

Aufgabe 3.4Z: Verschiedene Allpässe