Aufgaben:Aufgabe 4.5Z: Nochmals Impulsantwort: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 4.5Z Nochmals Impulsantwort nach Aufgabe 4.5Z: Nochmals Impulsantwort) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1815__LZI_Z_4_5.png|right|Impulsantwort eines Koaxialkabels]] | + | [[Datei:P_ID1815__LZI_Z_4_5.png|right|frame|Impulsantwort eines Koaxialkabels (Darstellung mit bzw. ohne Laufzeit)]] |
| − | Wir betrachten wieder wie in der [[Aufgaben:4.5_Koaxialkabel_–_Impulsantwort|Aufgabe 4.5]] ein binäres Übertragungssystem mit der Bitrate $R$ und der Symboldauer $T= 1/R$. Als Übertragungsmedium wird ein Normalkoaxialkabel (Innendurchmesser: 2.6 mm, Außendurchmesser: 9.5 mm) der Länge $l = 1 \ \rm km$ mit folgendem Frequenzgang verwendet: | + | Wir betrachten wieder wie in der [[Aufgaben:4.5_Koaxialkabel_–_Impulsantwort|Aufgabe 4.5]] ein binäres Übertragungssystem mit der Bitrate $R$ und der Symboldauer $T= 1/R$. |
| − | $$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1 \hspace{0.05cm}\cdot \hspace{0.05cm} f | + | |
| + | Als Übertragungsmedium wird ein Normalkoaxialkabel (Innendurchmesser: 2.6 mm, Außendurchmesser: 9.5 mm) der Länge $l = 1 \ \rm km$ mit folgendem Frequenzgang verwendet: | ||
| + | :$$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1 \hspace{0.05cm}\cdot \hspace{0.05cm} f | ||
\hspace{0.05cm}\cdot \hspace{0.05cm}l} | \hspace{0.05cm}\cdot \hspace{0.05cm}l} | ||
\cdot {\rm e}^{- \alpha_2 \hspace{0.01cm} | \cdot {\rm e}^{- \alpha_2 \hspace{0.01cm} | ||
| Zeile 14: | Zeile 16: | ||
\hspace{0.05cm}\cdot \hspace{0.05cm}l} | \hspace{0.05cm}\cdot \hspace{0.05cm}l} | ||
= H_1(f) \cdot H_2(f) \cdot H_3(f)$$ | = H_1(f) \cdot H_2(f) \cdot H_3(f)$$ | ||
| − | |||
Die Teilfrequenzgänge $H_1(f)$, $H_2(f)$ und $H_3(f)$ dienen hier nur als Abkürzung. Die Leitungsparameter lauten: | Die Teilfrequenzgänge $H_1(f)$, $H_2(f)$ und $H_3(f)$ dienen hier nur als Abkürzung. Die Leitungsparameter lauten: | ||
| − | $$\beta_1 = 21.78\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm}, \hspace{0.2cm} | + | :$$\beta_1 = 21.78\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm}, \hspace{0.2cm} |
\alpha_2 = 0.2722\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm},\hspace{0.2cm} | \alpha_2 = 0.2722\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm},\hspace{0.2cm} | ||
\beta_2 = 0.2722\, \frac{\rm rad}{\rm km \cdot \sqrt{MHz}} | \beta_2 = 0.2722\, \frac{\rm rad}{\rm km \cdot \sqrt{MHz}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
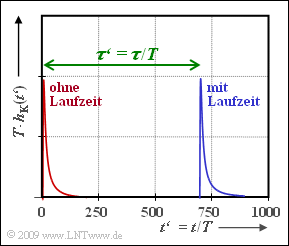
| − | Die Grafik zeigt die resultierende Impulsantwort $h_{\rm K}(t')$, wobei $t' = t/T$ die normierte Zeit darstellt. Ohne Berücksichtigung der (normierten) Phasenlaufzeit $\tau' = \tau/T$ kann $h_{\rm K}(t')$ wie folgt geschrieben werden: | + | Die Grafik zeigt die resultierende Impulsantwort $h_{\rm K}(t\hspace{0.03cm}')$, wobei $t\hspace{0.03cm}' = t/T$ die normierte Zeit darstellt. Ohne Berücksichtigung der (normierten) Phasenlaufzeit $\tau\hspace{0.03cm}' = \tau/T$ kann $h_{\rm K}(t\hspace{0.03cm}')$ wie folgt geschrieben werden: |
| − | $$h_{\rm K}(t') = \frac {1}{T} \cdot \frac { | + | :$$h_{\rm K}(t') = \frac {1}{T} \cdot \frac {a_\rm \star/\pi}{ \sqrt{2 |
| − | \hspace{0.05cm}t'^3}}\cdot {\rm exp} \left [ -\frac { | + | \hspace{0.05cm}t'^3}}\cdot {\rm exp} \left [ -\frac {a_\rm \star^2}{ {2\pi |
\hspace{0.05cm}t'}} \right ] \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} | \hspace{0.05cm}t'}} \right ] \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} | ||
| − | {\rm mit}\hspace{0.15cm}{ | + | {\rm mit}\hspace{0.15cm}{a}_{\rm \star}\hspace{0.15cm} |
{\rm in}\hspace{0.15cm} | {\rm in}\hspace{0.15cm} | ||
{\rm Neper}\hspace{0.05cm}.$$ | {\rm Neper}\hspace{0.05cm}.$$ | ||
| − | Diese Gleichung gibt die Fourierrücktransformierte des Produkts $H_2(f) \cdot H_3(f)$ an. Verwendet ist dabei die charakteristische Kabeldämpfung ${ | + | Diese Gleichung gibt die Fourierrücktransformierte des Produkts $H_2(f) \cdot H_3(f)$ an. Verwendet ist dabei die charakteristische Kabeldämpfung ${a}_{\rm \star} = \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$ |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Eigenschaften_von_Koaxialkabeln|Eigenschaften von Koaxialkabeln]]. | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Eigenschaften_von_Koaxialkabeln|Eigenschaften von Koaxialkabeln]]. | ||
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | *Sie können zur Überprüfung Ihrer Ergebnisse das | + | *Sie können zur Überprüfung Ihrer Ergebnisse das interaktive Applet [[Applets:Zeitverhalten_von_Kupferkabeln|Zeitverhalten von Kupferkabeln]] benutzen. |
*In der [[Aufgaben:4.5_Koaxialkabel_–_Impulsantwort|Aufgabe 4.5]] wurde der Maximalwert der normierten Impulsantwort wie folgt berechnet: | *In der [[Aufgaben:4.5_Koaxialkabel_–_Impulsantwort|Aufgabe 4.5]] wurde der Maximalwert der normierten Impulsantwort wie folgt berechnet: | ||
| − | $${\rm Max}[T \cdot h_{\rm K}(t)] = \frac {\sqrt{13.5 \pi} \cdot {\rm e}^{-1.5} }{{ | + | :$${\rm Max}\, [T \cdot h_{\rm K}(t)] = \frac {\sqrt{13.5 \pi} \cdot {\rm e}^{-1.5} }{{a}_{\rm \star}^2} \approx |
| − | \frac {1.453 }{{ | + | \frac {1.453 }{{a}_{\rm \star}^2} \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} |
| − | {\rm mit}\hspace{0.15cm}{ | + | {\rm mit}\hspace{0.15cm}{a}_{\rm \star}\hspace{0.15cm} |
{\rm in}\hspace{0.15cm} | {\rm in}\hspace{0.15cm} | ||
{\rm Neper}\hspace{0.05cm}.$$ | {\rm Neper}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| Zeile 46: | Zeile 54: | ||
<quiz display=simple> | <quiz display=simple> | ||
{Welcher Teilfrequenzgang ist für die Phasenlaufzeit $\tau$ verantwortlich? | {Welcher Teilfrequenzgang ist für die Phasenlaufzeit $\tau$ verantwortlich? | ||
| − | |type=" | + | |type="()"} |
+ $H_1(f)$, | + $H_1(f)$, | ||
- $H_2(f)$, | - $H_2(f)$, | ||
| Zeile 52: | Zeile 60: | ||
| − | {Bestimmen Sie die Bitrate des Binärsystems, wenn $\tau' = \tau/T = 694$ beträgt. | + | {Bestimmen Sie die Bitrate des Binärsystems, wenn $\tau\hspace{0.03cm}' = \tau/T = 694$ beträgt. |
|type="{}"} | |type="{}"} | ||
| − | $R \ =$ { 20 3% } $\ \rm Mbit/s$ | + | $R \ = \ $ { 20 3% } $\ \rm Mbit/s$ |
| − | {Geben Sie die charakteristische Kabeldämpfung ${ | + | {Geben Sie die charakteristische Kabeldämpfung ${a}_{\rm \star}$ zur gemeinsamen Beschreibung der Frequenzgänge $H_2(f)$ und $H_3(f)$ an. |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | ${a}_{\rm \star} \ = \ $ { 8.6 3% } $\ \rm Np$ |
{Bestimmen Sie den (normierten) Maximalwert der Impulsantwort. | {Bestimmen Sie den (normierten) Maximalwert der Impulsantwort. | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Max}[T \cdot h_{\rm K}(t)] \ =$ { 0.02 3% } | + | ${\rm Max}\, [T \cdot h_{\rm K}(t)] \ = \ $ { 0.02 3% } |
Version vom 28. März 2018, 15:50 Uhr
Wir betrachten wieder wie in der Aufgabe 4.5 ein binäres Übertragungssystem mit der Bitrate $R$ und der Symboldauer $T= 1/R$.
Als Übertragungsmedium wird ein Normalkoaxialkabel (Innendurchmesser: 2.6 mm, Außendurchmesser: 9.5 mm) der Länge $l = 1 \ \rm km$ mit folgendem Frequenzgang verwendet:
- $$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1 \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot {\rm e}^{- \alpha_2 \hspace{0.01cm} \sqrt{f} \hspace{0.05cm}l} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2 \hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} = H_1(f) \cdot H_2(f) \cdot H_3(f)$$
Die Teilfrequenzgänge $H_1(f)$, $H_2(f)$ und $H_3(f)$ dienen hier nur als Abkürzung. Die Leitungsparameter lauten:
- $$\beta_1 = 21.78\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm},\hspace{0.2cm} \beta_2 = 0.2722\, \frac{\rm rad}{\rm km \cdot \sqrt{MHz}} \hspace{0.05cm}.$$
Die Grafik zeigt die resultierende Impulsantwort $h_{\rm K}(t\hspace{0.03cm}')$, wobei $t\hspace{0.03cm}' = t/T$ die normierte Zeit darstellt. Ohne Berücksichtigung der (normierten) Phasenlaufzeit $\tau\hspace{0.03cm}' = \tau/T$ kann $h_{\rm K}(t\hspace{0.03cm}')$ wie folgt geschrieben werden:
- $$h_{\rm K}(t') = \frac {1}{T} \cdot \frac {a_\rm \star/\pi}{ \sqrt{2 \hspace{0.05cm}t'^3}}\cdot {\rm exp} \left [ -\frac {a_\rm \star^2}{ {2\pi \hspace{0.05cm}t'}} \right ] \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} {\rm mit}\hspace{0.15cm}{a}_{\rm \star}\hspace{0.15cm} {\rm in}\hspace{0.15cm} {\rm Neper}\hspace{0.05cm}.$$
Diese Gleichung gibt die Fourierrücktransformierte des Produkts $H_2(f) \cdot H_3(f)$ an. Verwendet ist dabei die charakteristische Kabeldämpfung ${a}_{\rm \star} = \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$
Hinweise:
- Die Aufgabe gehört zum Kapitel Eigenschaften von Koaxialkabeln.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Sie können zur Überprüfung Ihrer Ergebnisse das interaktive Applet Zeitverhalten von Kupferkabeln benutzen.
- In der Aufgabe 4.5 wurde der Maximalwert der normierten Impulsantwort wie folgt berechnet:
- $${\rm Max}\, [T \cdot h_{\rm K}(t)] = \frac {\sqrt{13.5 \pi} \cdot {\rm e}^{-1.5} }{{a}_{\rm \star}^2} \approx \frac {1.453 }{{a}_{\rm \star}^2} \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} {\rm mit}\hspace{0.15cm}{a}_{\rm \star}\hspace{0.15cm} {\rm in}\hspace{0.15cm} {\rm Neper}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
(2) Entsprechend dem Angabenblatt gilt: $$2\pi \cdot f \cdot \tau = \beta_1 \cdot f \cdot l \Rightarrow \hspace{0.3cm}\tau= \frac {\beta_1 \cdot l}{2\pi} = \frac {21.78\, {\rm rad}/{({\rm km \cdot MHz})}\cdot 10\,{\rm km}}{2\pi} = 34.7\,{\rm \mu s}$$ $$\Rightarrow \hspace{0.3cm}\tau '= {\tau}/{T} = 694 \Rightarrow \hspace{0.3cm} T = \frac {34.7\,{\rm \mu s}}{700} \approx 0.05\,{\rm \mu s}\hspace{0.05cm}.$$ Die Bitrate ist gleich dem Kehrwert der Symboldauer: $\underline{R = 20 \ \rm Mbit/s}$.
(3) Für die charakteristische Kabeldämpfung erhält man somit:
$${\rm a}_{\rm \star} = \alpha_2 \cdot \sqrt {R/2} \cdot l =
0.2722\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}} \cdot \sqrt {10\,{\rm MHz}} \cdot 10\,{\rm km} \hspace{0.15cm}\underline{\approx
8.6\,{\rm Np}}\hspace{0.05cm}.$$
Der entsprechende dB–Wert ist $75 \ \rm dB$.
(4) Mit der angegebenen Gleichung und dem Ergebnis der Teilaufgabe (3) ergibt sich: $${\rm Max}[T \cdot h_{\rm K}(t)] \approx \frac {1.453 }{{\rm a}_{\rm \star}^2} = \frac {1.453 }{8.6^2} \hspace{0.15cm}\underline{ \approx 0.02}\hspace{0.05cm}.$$
(5) Richtig ist nur Aussage 1: $H_1(f)$ beschreibt die frequenzunabhängige Laufzeit, die keine Verzerrung zur Folge hat.
Dagegen sollte man zur Berechnung der Impulsantwort auf keinen Fall auf $H_2(f)$ oder $H_3(f)$ verzichten, da es sonst es zu gravierenden Fehlern kommen würde:
- Die Impulsantwort $h_2(t)$ als die Fourierrücktransformierte von $H_2(f)$ ist eine gerade Funktion mit dem Maximum bei $t = 0$ und erstreckt sich in beide Richtungen über Hunderte von Symbolen.
- Dagegen ist die Fourierrücktransformierte von $H_3(f)$ eine ungerade Funktion mit einer Sprungstelle bei $t = 0$. Für $t > 0$ fällt $h_3(t)$ ähnlich – aber nicht exakt – wie eine Exponentialfunktion ab. Für negative Zeiten $t$ gilt $h_3(t) = - h_3(|t|)$.
- Erst die Faltung $h_2(t) \star h_3(t)$ liefert die kausale Impulsantwort, allerdings ohne die Phasenlaufzeit $\tau$, die durch $H_1(f)$ berücksichtigt wird.