Stochastische Signaltheorie/Linearkombinationen von Zufallsgrößen: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
|||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Voraussetzungen und Mittelwerte== | ==Voraussetzungen und Mittelwerte== | ||
| + | <br> | ||
In diesem Kapitel „ Linearkombinationen von Zufallsgrößen ” gehen wir von den folgenden Annahmen aus: | In diesem Kapitel „ Linearkombinationen von Zufallsgrößen ” gehen wir von den folgenden Annahmen aus: | ||
| − | *Die Zufallsgrößen $u$ und $v$ seien jeweils mittelwertfrei ⇒ $m_u = m_v = 0$ und zudem statistisch unabhängig voneinander ⇒ $ρ_{uv} = 0$. | + | *Die Zufallsgrößen $u$ und $v$ seien jeweils mittelwertfrei ⇒ $m_u = m_v = 0$ und zudem statistisch unabhängig voneinander ⇒ $ρ_{uv} = 0$. |
*Die beiden Zufallsgrößen $u$ und $v$ besitzen jeweils gleiche Streuung $σ$. Über die Art der Verteilung wird keine Aussage getroffen. | *Die beiden Zufallsgrößen $u$ und $v$ besitzen jeweils gleiche Streuung $σ$. Über die Art der Verteilung wird keine Aussage getroffen. | ||
*Die beiden Zufallsgrößen $x$ und $y$ seien Linearkombinationen von $u$ und $v$, wobei gilt: | *Die beiden Zufallsgrößen $x$ und $y$ seien Linearkombinationen von $u$ und $v$, wobei gilt: | ||
| Zeile 19: | Zeile 20: | ||
==Resultierender Korrelationskoeffizient== | ==Resultierender Korrelationskoeffizient== | ||
| − | Betrachten wir nun die '''Varianzen''' nach den Linearkombinationen. Für die Zufallsgröße $x$ gilt unabhängig vom Parameter $C$: | + | <br> |
| + | Betrachten wir nun die '''Varianzen''' der Zufallsgrößen nach den Linearkombinationen. Für die Zufallsgröße $x$ gilt unabhängig vom Parameter $C$: | ||
:$$\sigma _x ^2 = {\rm E}[x ^{\rm 2}] = A^{\rm 2} \cdot {\rm E}[u^{\rm 2}] + B^{\rm 2} \cdot {\rm E}[v^{\rm 2}] + {\rm 2} \cdot A \cdot B \cdot {\rm E}[u \cdot v].$$ | :$$\sigma _x ^2 = {\rm E}[x ^{\rm 2}] = A^{\rm 2} \cdot {\rm E}[u^{\rm 2}] + B^{\rm 2} \cdot {\rm E}[v^{\rm 2}] + {\rm 2} \cdot A \cdot B \cdot {\rm E}[u \cdot v].$$ | ||
| Zeile 31: | Zeile 33: | ||
Die '''Kovarianz''' $μ_{xy}$ ist bei mittelwertfreien Zufallsgrößen $x$ und $y$ ⇒ $C = F = 0$ identisch mit dem gemeinsamen Moment $m_{xy}$: | Die '''Kovarianz''' $μ_{xy}$ ist bei mittelwertfreien Zufallsgrößen $x$ und $y$ ⇒ $C = F = 0$ identisch mit dem gemeinsamen Moment $m_{xy}$: | ||
:$$\mu_{xy } = m_{xy } = {\rm E}[x \cdot y] = {\rm E}[(A \cdot u + B \cdot v)(D \cdot u + E \cdot v)].$$ | :$$\mu_{xy } = m_{xy } = {\rm E}[x \cdot y] = {\rm E}[(A \cdot u + B \cdot v)(D \cdot u + E \cdot v)].$$ | ||
| − | Beachten Sie hierbei, dass E[ | + | Beachten Sie hierbei, dass ${\rm E}[ \text{...} ]$ einen Erwartungswert bezeichnet, während $E$ eine Variable beschreibt. Nach Auswertung dieser Gleichung in analoger Weise zu oben folgt daraus: |
:$$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } | :$$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm} | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
| Zeile 38: | Zeile 40: | ||
Schließen wir die Sonderfälle $A = B = 0$ (d. h. $x ≡ 0$ ) sowie $D = E = 0$ (d. h. $y ≡ 0$ ) aus, so liefert die Gleichung stets eindeutige Werte für den Korrelationskoeffizienten im Bereich $–1 ≤ ρ_{xy} ≤ +1$. | Schließen wir die Sonderfälle $A = B = 0$ (d. h. $x ≡ 0$ ) sowie $D = E = 0$ (d. h. $y ≡ 0$ ) aus, so liefert die Gleichung stets eindeutige Werte für den Korrelationskoeffizienten im Bereich $–1 ≤ ρ_{xy} ≤ +1$. | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ | ||
| + | Setzen wir zum Beispiel $A = E = 0$, so ergibt sich der Korrelationskoeffizient $ρ_{xy} = 0$. Dieses Ergebnis ist einsichtig: | ||
| + | *Nun hängt $x$ nur noch von $v$ und $y$ ausschließlich von $u$ ab. | ||
| + | *Da aber $u$ und $v$ als statistisch unabhängig angenommen wurden, bestehen keine Beziehungen zwischen $x$ und $y$. | ||
| + | *Ebenso ergibt sich $ρ_{xy} = 0$ für die Kombination $B = D = 0$.}} | ||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel 2:}$ Die Konstellation $B = E = 0$ führt dazu, dass sowohl $x$ als auch $y$ nur noch von $u$ abhängen. In diesem Fall ergibt sich für den Korrelationskoeffizienten $ρ_{xy} = ±1$: | |
| − | + | :$$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2} } } = \frac {A \cdot D }{\vert A\vert \cdot \vert D\vert } =\pm 1. $$ | |
| − | $$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2}}} = \frac {A \cdot D }{ | ||
*Besitzen $A$ und $D$ gleiches Vorzeichen, so ist $ρ_{xy} = +1$. | *Besitzen $A$ und $D$ gleiches Vorzeichen, so ist $ρ_{xy} = +1$. | ||
| − | *Bei unterschiedlichen Vorzeichen ergibt sich der Korrelationskoeffizient $ | + | *Bei unterschiedlichen Vorzeichen ergibt sich der Korrelationskoeffizient $-1$. |
| − | *Auch für $A = D = 0$ ergibt sich der Koeffizient $ρ_{xy} = ±1$. | + | *Auch für $A = D = 0$ ergibt sich der Koeffizient $ρ_{xy} = ±1$. }} |
| − | |||
==Erzeugung korrelierter Zufallsgrößen== | ==Erzeugung korrelierter Zufallsgrößen== | ||
| + | <br> | ||
Die [[Stochastische_Signaltheorie/Linearkombinationen_von_Zufallsgrößen#Resultierender_Korrelationskoeffizient|Gleichungen der letzten Seite]] können zur Erzeugung einer zweidimensionalen Zufallsgröße $(x, y)$ mit vorgegebenen Kenngrößen $σ_x$, $σ_y$ und $ρ_{xy}$ genutzt werden. | Die [[Stochastische_Signaltheorie/Linearkombinationen_von_Zufallsgrößen#Resultierender_Korrelationskoeffizient|Gleichungen der letzten Seite]] können zur Erzeugung einer zweidimensionalen Zufallsgröße $(x, y)$ mit vorgegebenen Kenngrößen $σ_x$, $σ_y$ und $ρ_{xy}$ genutzt werden. | ||
| − | * | + | *Werden außer diesen drei Sollwerten keine weiteren Voraussetzungen getroffen, so ist einer der vier Koeffizienten $A, B, D$ und $E$ frei wählbar. Im Folgenden wird stets willkürlich $E = 0$ gesetzt. |
| − | *Mit der weiteren Festlegung, dass die statistisch | + | *Mit der weiteren Festlegung, dass die statistisch unabhängigen Zufallsgrößen $u$ und $v$ jeweils die Streuung $σ =1$ aufweisen, erhält man: |
:$$D = \sigma_y, \hspace{0.5cm} A = \sigma_x \cdot \rho_{xy}, \hspace{0.5cm} B = \sigma_x \cdot \sqrt {1-\rho_{xy}^2}.$$ | :$$D = \sigma_y, \hspace{0.5cm} A = \sigma_x \cdot \rho_{xy}, \hspace{0.5cm} B = \sigma_x \cdot \sqrt {1-\rho_{xy}^2}.$$ | ||
*Bei $σ ≠ 1$ sind diese Werte jeweils noch durch $σ$ zu dividieren. | *Bei $σ ≠ 1$ sind diese Werte jeweils noch durch $σ$ zu dividieren. | ||
| − | {{ | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 3:}$ | |
| + | Wir gehen stets von mittelwertfreien Gaußschen Zufallsgrößen $u$ und $v$ aus. Beide besitzen die Varianz $σ^2 = 1$. | ||
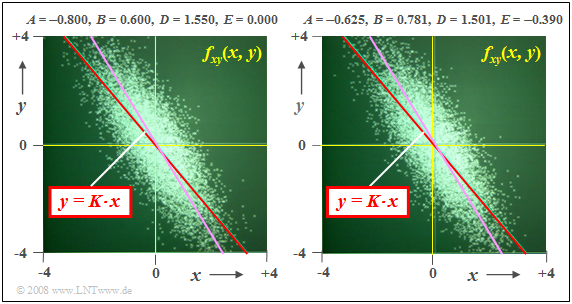
| − | '''( | + | '''(a)''' Zur Erzeugung einer 2D–Zufallsgröße mit den gewünschten Kennwerten $σ_x =1$, $σ_y = 1.55$ und $ρ_{xy} = -0.8$ eignet sich zum Beispiel der Parametersatz $A = -0.8, \; B = 0.6, \; D = 1.55, E = 0$, der dem linken Bild zugrundeliegt. |
| − | *Die Korrelationsgerade $K(x)$ ist rot dargestellt. Sie verläuft unter einem Winkel von etwa $ | + | *Die Korrelationsgerade $K(x)$ ist rot dargestellt. Sie verläuft unter einem Winkel von etwa $-50^\circ$. |
*Violett eingezeichnet ist die Ellipsenhauptachse, die etwas oberhalb der Korrelationsgeraden liegt. | *Violett eingezeichnet ist die Ellipsenhauptachse, die etwas oberhalb der Korrelationsgeraden liegt. | ||
| − | [[Datei:P_ID419__Sto_T_4_3_S3_neu.png |frame| Per Linearkombination erzeugte 2D-Zufallsgrößen]] | + | [[Datei:P_ID419__Sto_T_4_3_S3_neu.png|center |frame| Per Linearkombination erzeugte 2D-Zufallsgrößen]] |
| − | '''( | + | '''(b)''' Der Parametersatz für die rechte Grafik lautet: $A = -0.625, B = 0.781, D = 1.501, E = -0.390$. |
*Im statistischen Sinne erhält man das gleiche Resultat, auch wenn sich die beiden Punktwolken im Detail unterscheiden. | *Im statistischen Sinne erhält man das gleiche Resultat, auch wenn sich die beiden Punktwolken im Detail unterscheiden. | ||
| − | *Insbesondere ergibt sich bezüglich Korrelationsgerade und Ellipsenhauptachse kein Unterschied zum | + | *Insbesondere ergibt sich bezüglich Korrelationsgerade und Ellipsenhauptachse kein Unterschied zum Parametersatz '''(a)'''. }} |
| − | |||
| − | |||
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:4.7 Gewichtete Summe und Differenz|Aufgabe 4.7: Gewichtete Summe und Differenz]] | ||
| − | + | [[Aufgaben:4.7Z Erzeugung einer 2D–WDF|Aufgabe 4.7Z: Erzeugung einer 2D–WDF]] | |
| − | |||
| − | [[Aufgaben:4.7Z Erzeugung einer 2D–WDF| | ||
| − | [[Aufgaben:4.8 Rautenförmige 2D-WDF|Aufgabe 4.8: | + | [[Aufgaben:4.8 Rautenförmige 2D-WDF|Aufgabe 4.8: Rautenförmige 2D-WDF]] |
| − | [[Aufgaben:4.8Z AWGN-Kanal| | + | [[Aufgaben:4.8Z AWGN-Kanal|Aufgabe 4.8Z: AWGN-Kanal]] |
{{Display}} | {{Display}} | ||
Version vom 11. April 2018, 09:22 Uhr
Inhaltsverzeichnis
Voraussetzungen und Mittelwerte
In diesem Kapitel „ Linearkombinationen von Zufallsgrößen ” gehen wir von den folgenden Annahmen aus:
- Die Zufallsgrößen $u$ und $v$ seien jeweils mittelwertfrei ⇒ $m_u = m_v = 0$ und zudem statistisch unabhängig voneinander ⇒ $ρ_{uv} = 0$.
- Die beiden Zufallsgrößen $u$ und $v$ besitzen jeweils gleiche Streuung $σ$. Über die Art der Verteilung wird keine Aussage getroffen.
- Die beiden Zufallsgrößen $x$ und $y$ seien Linearkombinationen von $u$ und $v$, wobei gilt:
- $$x=A \cdot u + B \cdot v + C,$$
- $$y=D \cdot u + E \cdot v + F.$$
Für die (linearen) Mittelwerte der neuen Zufallsgrößen $x$ und $y$ erhält man nach den allgemeinen Rechenregeln für Erwartungswerte:
- $$m_x =A \cdot m_u + B \cdot m_v + C =C,$$
- $$m_y =D \cdot m_u + E \cdot m_v + F =F.$$
Die Koeffizienten $C$ und $F$ geben somit lediglich die Mittelwerte von $x$ und $y$ an. Beide werden auf den folgenden Seiten stets zu $0$ gesetzt.
Resultierender Korrelationskoeffizient
Betrachten wir nun die Varianzen der Zufallsgrößen nach den Linearkombinationen. Für die Zufallsgröße $x$ gilt unabhängig vom Parameter $C$:
- $$\sigma _x ^2 = {\rm E}[x ^{\rm 2}] = A^{\rm 2} \cdot {\rm E}[u^{\rm 2}] + B^{\rm 2} \cdot {\rm E}[v^{\rm 2}] + {\rm 2} \cdot A \cdot B \cdot {\rm E}[u \cdot v].$$
Die Erwartungswerte von $u^2$ und $v^2$ sind definitionsgemäß jeweils gleich $σ^2$, weil $u$ und $v$ mittelwertfrei sind. Da $u$ und $v$ zudem als statistisch unabhängig vorausgesetzt werden, kann man für den Erwartungswert des Produktes auch schreiben:
- $${\rm E}[u \cdot v] = {\rm E}[u] \cdot {\rm E}[v] = m_u \cdot m_v = \rm 0.$$
Damit erhält man für die Varianzen der durch Linearkombinationen gebildeten Zufallsgrößen:
- $$\sigma _x ^2 =(A^2 + B^2) \cdot \sigma ^2,$$
- $$\sigma _y ^2 =(D^2 + E^2) \cdot \sigma ^2.$$
Die Kovarianz $μ_{xy}$ ist bei mittelwertfreien Zufallsgrößen $x$ und $y$ ⇒ $C = F = 0$ identisch mit dem gemeinsamen Moment $m_{xy}$:
- $$\mu_{xy } = m_{xy } = {\rm E}[x \cdot y] = {\rm E}[(A \cdot u + B \cdot v)(D \cdot u + E \cdot v)].$$
Beachten Sie hierbei, dass ${\rm E}[ \text{...} ]$ einen Erwartungswert bezeichnet, während $E$ eine Variable beschreibt. Nach Auswertung dieser Gleichung in analoger Weise zu oben folgt daraus:
- $$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \rho_{xy } = \frac{\rho_{xy }}{\sigma_x \cdot \sigma_y} = \frac {A \cdot D + B \cdot E}{\sqrt{(A^{\rm 2}+B^{\rm 2})(D^{\rm 2}+E^{\rm 2})}}. $$
Schließen wir die Sonderfälle $A = B = 0$ (d. h. $x ≡ 0$ ) sowie $D = E = 0$ (d. h. $y ≡ 0$ ) aus, so liefert die Gleichung stets eindeutige Werte für den Korrelationskoeffizienten im Bereich $–1 ≤ ρ_{xy} ≤ +1$.
$\text{Beispiel 1:}$ Setzen wir zum Beispiel $A = E = 0$, so ergibt sich der Korrelationskoeffizient $ρ_{xy} = 0$. Dieses Ergebnis ist einsichtig:
- Nun hängt $x$ nur noch von $v$ und $y$ ausschließlich von $u$ ab.
- Da aber $u$ und $v$ als statistisch unabhängig angenommen wurden, bestehen keine Beziehungen zwischen $x$ und $y$.
- Ebenso ergibt sich $ρ_{xy} = 0$ für die Kombination $B = D = 0$.
$\text{Beispiel 2:}$ Die Konstellation $B = E = 0$ führt dazu, dass sowohl $x$ als auch $y$ nur noch von $u$ abhängen. In diesem Fall ergibt sich für den Korrelationskoeffizienten $ρ_{xy} = ±1$:
- $$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2} } } = \frac {A \cdot D }{\vert A\vert \cdot \vert D\vert } =\pm 1. $$
- Besitzen $A$ und $D$ gleiches Vorzeichen, so ist $ρ_{xy} = +1$.
- Bei unterschiedlichen Vorzeichen ergibt sich der Korrelationskoeffizient $-1$.
- Auch für $A = D = 0$ ergibt sich der Koeffizient $ρ_{xy} = ±1$.
Erzeugung korrelierter Zufallsgrößen
Die Gleichungen der letzten Seite können zur Erzeugung einer zweidimensionalen Zufallsgröße $(x, y)$ mit vorgegebenen Kenngrößen $σ_x$, $σ_y$ und $ρ_{xy}$ genutzt werden.
- Werden außer diesen drei Sollwerten keine weiteren Voraussetzungen getroffen, so ist einer der vier Koeffizienten $A, B, D$ und $E$ frei wählbar. Im Folgenden wird stets willkürlich $E = 0$ gesetzt.
- Mit der weiteren Festlegung, dass die statistisch unabhängigen Zufallsgrößen $u$ und $v$ jeweils die Streuung $σ =1$ aufweisen, erhält man:
- $$D = \sigma_y, \hspace{0.5cm} A = \sigma_x \cdot \rho_{xy}, \hspace{0.5cm} B = \sigma_x \cdot \sqrt {1-\rho_{xy}^2}.$$
- Bei $σ ≠ 1$ sind diese Werte jeweils noch durch $σ$ zu dividieren.
$\text{Beispiel 3:}$ Wir gehen stets von mittelwertfreien Gaußschen Zufallsgrößen $u$ und $v$ aus. Beide besitzen die Varianz $σ^2 = 1$.
(a) Zur Erzeugung einer 2D–Zufallsgröße mit den gewünschten Kennwerten $σ_x =1$, $σ_y = 1.55$ und $ρ_{xy} = -0.8$ eignet sich zum Beispiel der Parametersatz $A = -0.8, \; B = 0.6, \; D = 1.55, E = 0$, der dem linken Bild zugrundeliegt.
- Die Korrelationsgerade $K(x)$ ist rot dargestellt. Sie verläuft unter einem Winkel von etwa $-50^\circ$.
- Violett eingezeichnet ist die Ellipsenhauptachse, die etwas oberhalb der Korrelationsgeraden liegt.
(b) Der Parametersatz für die rechte Grafik lautet: $A = -0.625, B = 0.781, D = 1.501, E = -0.390$.
- Im statistischen Sinne erhält man das gleiche Resultat, auch wenn sich die beiden Punktwolken im Detail unterscheiden.
- Insbesondere ergibt sich bezüglich Korrelationsgerade und Ellipsenhauptachse kein Unterschied zum Parametersatz (a).
Aufgaben zum Kapitel
Aufgabe 4.7: Gewichtete Summe und Differenz
Aufgabe 4.7Z: Erzeugung einer 2D–WDF
Aufgabe 4.8: Rautenförmige 2D-WDF