Digitalsignalübertragung/Struktur des optimalen Empfängers: Unterschied zwischen den Versionen
| Zeile 318: | Zeile 318: | ||
Liegt ein $N$–dimensionales Modulationsverfahren vor, das heißt, es gilt mit $0 \le i \le M-1$ und $1 \le j \le N$: | Liegt ein $N$–dimensionales Modulationsverfahren vor, das heißt, es gilt mit $0 \le i \le M-1$ und $1 \le j \le N$: | ||
:$$s_i(t) = \sum\limits_{j = 1}^{N} s_{ij} \cdot \varphi_j(t) = s_{i1} \cdot \varphi_1(t) | :$$s_i(t) = \sum\limits_{j = 1}^{N} s_{ij} \cdot \varphi_j(t) = s_{i1} \cdot \varphi_1(t) | ||
| − | + s_{i2} \cdot \varphi_2(t) + ... + s_{iN} \cdot \varphi_N(t)\hspace{0.05cm}\hspace{0.3cm} | + | + s_{i2} \cdot \varphi_2(t) + \hspace{0.05cm}\text{...}\hspace{0.05cm} + s_{iN} \cdot \varphi_N(t)\hspace{0.05cm}\hspace{0.3cm} |
| − | \Rightarrow \hspace{0.3cm} \boldsymbol{ s}_i = \left(s_{i1}, s_{i2}, ... \hspace{0.05cm}, s_{iN}\right ) | + | \Rightarrow \hspace{0.3cm} \boldsymbol{ s}_i = \left(s_{i1}, s_{i2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, s_{iN}\right ) |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | so muss der Rauschvektor $\boldsymbol{ n}$ ebenfalls mit der Dimension $N$ angesetzt werden | + | so muss der Rauschvektor $\boldsymbol{ n}$ ebenfalls mit der Dimension $N$ angesetzt werden. Das gleiche gilt auch für den Empfangsvektor $\boldsymbol{ r}$: |
| − | :$$\boldsymbol{ n} = \left(n_{1}, n_{2}, ... \hspace{0.05cm}, n_{N}\right ) | + | :$$\boldsymbol{ n} = \left(n_{1}, n_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, n_{N}\right ) |
| − | \hspace{0.01cm},\hspace{0.2cm}\boldsymbol{ r} = \left(r_{1}, r_{2}, ... \hspace{0.05cm}, r_{N}\right )\hspace{0.05cm}.$$ | + | \hspace{0.01cm},\hspace{0.2cm}\boldsymbol{ r} = \left(r_{1}, r_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, r_{N}\right )\hspace{0.05cm}.$$ |
Die Wahrscheinlichkeitsdichtefunktion (WDF) lautet dann für den AWGN–Kanal mit der Realisierung $\boldsymbol{ \eta}$ des Rauschsignals | Die Wahrscheinlichkeitsdichtefunktion (WDF) lautet dann für den AWGN–Kanal mit der Realisierung $\boldsymbol{ \eta}$ des Rauschsignals | ||
| Zeile 332: | Zeile 332: | ||
und für die bedingte WDF in der Maximum–Likelihood–Entscheidungsregel ist anzusetzen: | und für die bedingte WDF in der Maximum–Likelihood–Entscheidungsregel ist anzusetzen: | ||
| − | :$$p_{\hspace{0.02cm}\boldsymbol{ r}\hspace{0. | + | :$$p_{\hspace{0.02cm}\boldsymbol{ r}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_i) \hspace{-0.1cm} = \hspace{0.1cm} |
| − | p_{\hspace{0.02cm} \boldsymbol{ n}\hspace{0. | + | p_{\hspace{0.02cm} \boldsymbol{ n}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} - \boldsymbol{ s}_i \hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}_i) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot |
{\rm exp} \left [ - \frac{|| \boldsymbol{ \rho} - \boldsymbol{ s}_i ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.$$ | {\rm exp} \left [ - \frac{|| \boldsymbol{ \rho} - \boldsymbol{ s}_i ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.$$ | ||
Die Gleichung ergibt sich aus der allgemeinen Darstellung der $N$–dimensionalen Gaußschen WDF im Abschnitt [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgr%C3%B6%C3%9Fen#Korrelationsmatrix|Korrelationsmatrix]] des Buches „Stochastische Signaltheorie” unter der Voraussetzung, dass die Komponenten unkorreliert (und somit statistisch unabhängig) sind. $||\boldsymbol{ \eta}||$ bezeichnet man als die ''Norm'' (Länge) des Vektors $\boldsymbol{ \eta}$.<br> | Die Gleichung ergibt sich aus der allgemeinen Darstellung der $N$–dimensionalen Gaußschen WDF im Abschnitt [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgr%C3%B6%C3%9Fen#Korrelationsmatrix|Korrelationsmatrix]] des Buches „Stochastische Signaltheorie” unter der Voraussetzung, dass die Komponenten unkorreliert (und somit statistisch unabhängig) sind. $||\boldsymbol{ \eta}||$ bezeichnet man als die ''Norm'' (Länge) des Vektors $\boldsymbol{ \eta}$.<br> | ||
| + | [[Datei:P ID2012 Dig T 4 2 S8 version1.png|right|frame|Zweidimensionale Gauß–WDF]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ | + | $\text{Beispiel 2:}$ |
Rechts dargestellt ist die zweidimensionale Gauß–WDF $p_{\boldsymbol{ n} } (\boldsymbol{ \eta})$ der 2D–Zufallsgröße $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$. Beliebige Realisierungen der Zufallsgröße $\boldsymbol{ n}$ werden mit $\boldsymbol{ \eta} = (\eta_1,\hspace{0.05cm}\eta_2)$ bezeichnet. | Rechts dargestellt ist die zweidimensionale Gauß–WDF $p_{\boldsymbol{ n} } (\boldsymbol{ \eta})$ der 2D–Zufallsgröße $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$. Beliebige Realisierungen der Zufallsgröße $\boldsymbol{ n}$ werden mit $\boldsymbol{ \eta} = (\eta_1,\hspace{0.05cm}\eta_2)$ bezeichnet. | ||
*Die Gleichung der dargestellten Glockenkurve lautet: | *Die Gleichung der dargestellten Glockenkurve lautet: | ||
:$$p_{n_1, n_2}(\eta_1, \eta_2) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot | :$$p_{n_1, n_2}(\eta_1, \eta_2) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot | ||
{\rm exp} \left [ - \frac{ \eta_1^2 + \eta_2^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}. $$ | {\rm exp} \left [ - \frac{ \eta_1^2 + \eta_2^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}. $$ | ||
| − | *Das Maximum dieser Funktion liegt bei $\eta_1 = \ | + | *Das Maximum dieser Funktion liegt bei $\eta_1 = \eta_2 = 0$ und hat den Wert $2\pi \cdot \sigma_n^2$. |
| + | *Mit $\sigma_n^2 = N_0/2$ lässt sich die 2D–WDF in Vektorform auch wie folgt schreiben: | ||
:$$p_{\boldsymbol{ n} }(\boldsymbol{ \eta}) = \frac{1}{\pi \cdot N_0 } \cdot | :$$p_{\boldsymbol{ n} }(\boldsymbol{ \eta}) = \frac{1}{\pi \cdot N_0 } \cdot | ||
{\rm exp} \left [ - \frac{\vert \vert \boldsymbol{ \eta} \vert \vert ^2}{N_0}\right ]\hspace{0.05cm}.$$ | {\rm exp} \left [ - \frac{\vert \vert \boldsymbol{ \eta} \vert \vert ^2}{N_0}\right ]\hspace{0.05cm}.$$ | ||
| Zeile 356: | Zeile 358: | ||
*Zirkulär symmetrisch bedeutet auch, dass Inphasekomponente $n_{\rm I}(t)$ und Quadraturkomponente $n_{\rm Q}(t)$ die gleiche Verteilung aufweisen und damit auch gleiche Varianz (Streuung) besitzen: | *Zirkulär symmetrisch bedeutet auch, dass Inphasekomponente $n_{\rm I}(t)$ und Quadraturkomponente $n_{\rm Q}(t)$ die gleiche Verteilung aufweisen und damit auch gleiche Varianz (Streuung) besitzen: | ||
| − | :$$ {\rm E} [ n_{\rm I}^2(t) ] = {\rm E} [ n_{\rm Q}^2(t)] = {\rm E}[ n_{\rm Q}^2(t) ] = \sigma_n^2 \hspace{0.05cm},\hspace{1cm}{\rm E} [ n(t) \cdot n^*(t) ]\hspace{0.1cm} = \hspace{0.1cm} {\rm E}[ n_{\rm I}^2(t) ] + {\rm E}[ n_{\rm Q}^2(t) ] = 2\sigma_n^2 \hspace{0.05cm}.$$}} | + | :$$ {\rm E} \big [ n_{\rm I}^2(t)\big ] = {\rm E}\big [ n_{\rm Q}^2(t)\big ] = {\rm E}\big [ n_{\rm Q}^2(t) \big ] = \sigma_n^2 \hspace{0.05cm},\hspace{1cm}{\rm E}\big [ n(t) \cdot n^*(t) \big ]\hspace{0.1cm} = \hspace{0.1cm} {\rm E}\big [ n_{\rm I}^2(t) \big ] + {\rm E}\big [ n_{\rm Q}^2(t)\big ] = 2\sigma_n^2 \hspace{0.05cm}.$$}} |
| − | Abschließend noch einige '' | + | Abschließend noch einige ''Bezeichnungsvarianten'' für Gaußsche Zufallsgrößen: |
:$$x ={\cal N}(\mu, \sigma^2) \hspace{-0.1cm}: \hspace{0.3cm}\text{reelle gaußverteilte Zufallsgröße, mit Mittelwert}\hspace{0.1cm}\mu \text { und Varianz}\hspace{0.15cm}\sigma^2 \hspace{0.05cm},$$ | :$$x ={\cal N}(\mu, \sigma^2) \hspace{-0.1cm}: \hspace{0.3cm}\text{reelle gaußverteilte Zufallsgröße, mit Mittelwert}\hspace{0.1cm}\mu \text { und Varianz}\hspace{0.15cm}\sigma^2 \hspace{0.05cm},$$ | ||
Version vom 12. Juni 2018, 15:01 Uhr
Inhaltsverzeichnis
- 1 Blockschaltbild und Voraussetzungen
- 2 Fundamentaler Ansatz zum optimalen Empfängerentwurf
- 3 Das Theorem der Irrelevanz
- 4 Einige Eigenschaften des AWGN-Kanals
- 5 Beschreibung des AWGN-Kanals durch orthonormale Basisfunktionen
- 6 Optimaler Empfänger für den AWGN-Kanal
- 7 Implementierungsaspekte
- 8 Wahrscheinlichkeitsdichtefunktion der Empfangswerte
- 9 N–dimensionales Gaußsches Rauschen
- 10 Aufgaben zum Kapitel
Blockschaltbild und Voraussetzungen
In diesem Kapitel wird die Struktur des optimalen Empfängers eines digitalen Übertragungssystems sehr allgemein hergeleitet, wobei
- das Modulationsverfahren und weitere Systemdetails nicht weiter spezifiziert werden,
- von den Basisfunktionen und der Signalraumdarstellung gemäß dem Kapitel Signale, Basisfunktionen und Vektorräume ausgegangen wird.
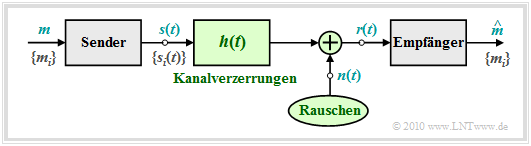
Zum obigen Blockschaltbild ist anzumerken:
- Der Symbolumfang der Quelle beträgt $M$ und der Symbolvorrat ist $\{m_i\}$ mit $i = 0$, ... , $M- 1$. Die zugehörigen Symbolwahrscheinlichkeiten ${\rm Pr}(m = m_i)$ seien auch dem Empfänger bekannt.
- Zur Nachrichtenübertragung stehen $M$ verschiedene Signalformen $s_i(t)$ zur Verfügung, wobei für die Laufvariable ebenfalls die Indizierung $i = 0$, ... , $M- 1$ gelten soll. Es besteht eine feste Beziehung zwischen den Nachrichten $\{m_i\}$ und den Signalen $\{s_i(t)\}$. Wird die Nachricht $m =m_i$ übertragen, so ist das Sendesignal $s(t) =s_i(t)$.
- Lineare Kanalverzerrungen sind in der obigen Grafik durch die Impulsantwort $h(t)$ berücksichtigt. Außerdem ist ein (irgendwie geartetes) Rauschen $n(t)$ wirksam. Mit diesen beiden die Übertragung störenden Effekten lässt sich das am Empfänger ankommende Signal $r(t)$ in folgender Weise angeben:
- $$r(t) = s(t) \star h(t) + n(t) \hspace{0.05cm}.$$
- Aufgabe des (optimalen) Empfängers ist es, anhand seines Eingangssignals $r(t)$ herauszufinden, welche der $M$ möglichen Nachrichten $m_i$ – bzw. welches der Signale $s_i(t)$ – gesendet wurde. Der vom Empfänger gefundene Schätzwert für $m$ wird durch ein Zirkumflex (französisch: Circonflexe) gekennzeichnet ⇒ $\hat{m}$.
$\text{Definition:}$ Man spricht von einem optimalen Empfänger, wenn die Symbolfehlerwahrscheinlichkeit den für die Randbedingungen kleinstmöglichsten Wert annimmt:
- $$p_{\rm S} = {\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm Minimum} \hspace{0.05cm}.$$
Hinweise:
- Im Folgenden wird meist der AWGN–Ansatz ⇒ $r(t) = s(t) + n(t)$ vorausgesetzt, was bedeutet, dass $h(t) = \delta(t)$ als verzerrungsfrei angenommen wird.
- Andernfalls könnten wir die Signale $s_i(t)$ als ${s_i}'(t) = s_i(t) \star h(t)$ neu definieren, also die deterministischen Kanalverzerrungen dem Sendesignal beaufschlagen.
Fundamentaler Ansatz zum optimalen Empfängerentwurf
Gegenüber dem auf der vorherigen Seite gezeigten Blockschaltbild führen wir nun einige wesentliche Verallgemeinerungen durch:
- Der Übertragungskanal wird durch die bedingte Wahrscheinlichkeitsdichtefunktion $p_{\hspace{0.02cm}r(t)\hspace{0.02cm} \vert \hspace{0.02cm}s(t)}$ beschrieben, welche die Abhängigkeit des Empfangssignals $r(t)$ vom Sendesignal $s(t)$ festlegt.
- Wurde nun ein ganz bestimmtes Signal $r(t) = \rho(t)$ empfangen, so hat der Empfänger die Aufgabe, anhand dieser Signalrealisierung $\rho(t)$ sowie der $M$ bedingten Wahrscheinlichkeitsdichtefunktionen
- $$p_{\hspace{0.05cm}r(t) \hspace{0.05cm} \vert \hspace{0.05cm} s(t) } (\rho(t) \hspace{0.05cm} \vert \hspace{0.05cm} s_i(t))\hspace{0.2cm}{\rm mit}\hspace{0.2cm} i = 0, \text{...} \hspace{0.05cm}, M-1$$
- unter Berücksichtigung aller möglichen Sendesignale $s_i(t)$ und deren Auftrittswahrscheinlichkeiten ${\rm Pr}(m = m_i)$ herauszufinden, welche der möglichen Nachrichten $m_i$ bzw. welches der möglichen Signale $s_i(t)$ am wahrscheinlichsten gesendet wurde.
- Die Schätzung des optimalen Empfängers ist also ganz allgemein bestimmt durch die Gleichung
- $$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} p_{\hspace{0.02cm}s(t) \hspace{0.05cm} \vert \hspace{0.05cm} r(t) } ( s_i(t) \hspace{0.05cm} \vert \hspace{0.05cm} \rho(t)) = {\rm arg} \max_i \hspace{0.1cm} p_{m \hspace{0.05cm} \vert \hspace{0.05cm} r(t) } ( \hspace{0.05cm}m_i\hspace{0.05cm} \vert \hspace{0.05cm}\rho(t))\hspace{0.05cm},$$
- wobei berücksichtigt ist, dass die gesendete Nachricht $m = m_i$ und das gesendete Signal $s(t) = s_i(t)$ eineindeutig ineinander übergeführt werden können.
$\text{In anderen Worten:}$ Der optimale Empfänger betrachtet diejenige Nachricht $m_i$ als die am wahrscheinlichsten gesendete, deren bedingte Wahrscheinlichkeitsdichtefunktion $p_{\hspace{0.02cm}m \hspace{0.05cm} \vert \hspace{0.05cm} r(t) }$ für das anliegende Empfangssignal $\rho(t)$ sowie unter der Annahme $m =m_i$ den größtmöglichen Wert annimmt.
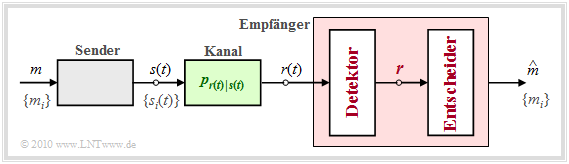
Bevor wir die obige Entscheidungsregel näher diskutieren, soll der optimale Empfänger entsprechend der Grafik noch in zwei Funktionsblöcke aufgeteilt werden:
- Der Detektor nimmt am Empfangssignal $r(t)$ verschiedene Messungen vor und fasst diese im Vektor $\boldsymbol{r}$ zusammen. Bei $K$ Messungen entspricht $\boldsymbol{r}$ einem Punkt im $K$–dimensionalen Vektorraum.
- Der Entscheider bildet abhängig von diesem Vektor den Schätzwert. Bei einem gegebenen Vektor $\boldsymbol{r} = \boldsymbol{\rho}$ lautet dabei die Entscheidungsregel:
- $$\hat{m} = {\rm arg}\hspace{0.05cm} \max_i \hspace{0.1cm} P_{m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}) \hspace{0.05cm}.$$
Im Gegensatz zur oberen Entscheidungsregel tritt nun eine bedingte Wahrscheinlichkeit $P_{m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} }$ anstelle der bedingten Wahrscheinlichkeitskeitsdichtefunktion (WDF) $p_{m\hspace{0.05cm} \vert \hspace{0.05cm}r(t)}$ auf. Beachten Sie bitte die Groß– bzw. Kleinschreibung für die unterschiedlichen Bedeutungen.
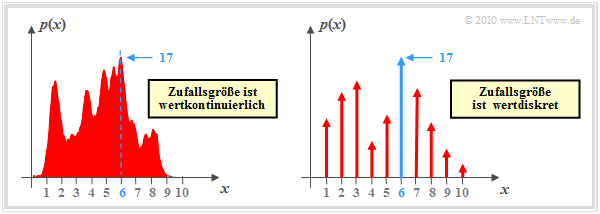
$\text{Beispiel 1:}$ Wir betrachten nun die Funktion $y = {\rm arg}\hspace{0.05cm} \max \ p(x)$, wobei $p(x)$ die Wahrscheinlichkeitsdichtefunktion (WDF) einer wertkontinuierlichen oder wertdiskreten Zufallsgröße $x$ beschreibt. Im zweiten Fall (rechte Grafik) besteht die WDF aus einer Summe von Diracfunktionen mit den Wahrscheinlichkeiten als Impulsgewichte.
Die Grafik zeigt beispielhafte Funktionen. In beiden Fällen liegt das WDF–Maximum $(17)$ bei $x = 6$:
- $$\max_i \hspace{0.1cm} p(x) = 17\hspace{0.05cm},$$
- $$y = {\rm \hspace{0.05cm}arg} \max_i \hspace{0.1cm} p(x) = 6\hspace{0.05cm}.$$
Die (bedingten) Wahrscheinlichkeiten in der Gleichung
- $$\hat{m} = {\rm arg}\hspace{0.05cm} \max_i \hspace{0.1cm} P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho})$$
sind a–Posteriori–Wahrscheinlichkeiten.
Mit dem Satz von Bayes kann hierfür geschrieben werden:
- $$P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}) = \frac{ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )}{p_{\boldsymbol{ r} } (\boldsymbol{\rho})} \hspace{0.05cm}.$$
Der Nennerterm ist für alle Alternativen $m_i$ gleich und muss für die Entscheidung nicht berücksichtigt werden. Damit erhält man folgende Regeln:
$\text{Satz:}$ Die Entscheidungsregel des optimalen Empfängers, auch bekannt als MAP–Empfänger (steht für Maximum–a–posteriori), lautet:
- $$\hat{m}_{\rm MAP} = {\rm \hspace{0.05cm} arg} \max_i \hspace{0.1cm} P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}) = {\rm \hspace{0.05cm}arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm} m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm} m_i )\big ]\hspace{0.05cm}.$$
Der Vorteil dieser Gleichung ist, dass die die Vorwärtsrichtung des Kanals beschreibende bedingte WDF $p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm} m }$ („Ausgang unter der Bedingung Eingang”) verwendet werden kann. Dagegen verwendet die erste Gleichung die Rückschlusswahrscheinlichkeiten $P_{\hspace{0.05cm}m\hspace{0.05cm} \vert \hspace{0.02cm} \boldsymbol{ r} } $ („Eingang unter der Bedingung Ausgang”).
$\text{Satz:}$ Ein Maximum–Likelihood–Empfänger (kurz ML–Empfänger) verwendet die Entscheidungsregel
- $$\hat{m}_{\rm ML} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )\hspace{0.05cm}.$$
Bei diesem werden die möglicherweise unterschiedlichen Auftrittswahrscheinlichkeiten ${\rm Pr}(m = m_i)$ für den Entscheidungsprozess nicht herangezogen, zum Beispiel, weil sie dem Empfänger nicht bekannt sind.
Im früheren Kapitel Optimale Empfängerstrategien finden Sie andere Herleitungen für diese Empfängertypen.
$\text{Fazit:}$ Bei gleichwahrscheinlichen Nachrichten $\{m_i\}$ ⇒ ${\rm Pr}(m = m_i) = 1/M$ ist der im Allgemeinen etwas schlechtere ML–Empfänger gleichwertig mit dem MAP–Empfänger:
- $$\hat{m}_{\rm MAP} = \hat{m}_{\rm ML} =\hspace{-0.1cm} {\rm\hspace{0.05cm} arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )\hspace{0.05cm}.$$
Das Theorem der Irrelevanz
Zu beachten ist, dass der auf der letzten Seite beschriebene Empfänger nur dann optimal ist, wenn auch der Detektor bestmöglich implementiert ist, das heißt, wenn durch den Übergang vom kontinuierlichen Signal $r(t)$ zum Vektor $\boldsymbol{r}$ keine Information verloren geht.
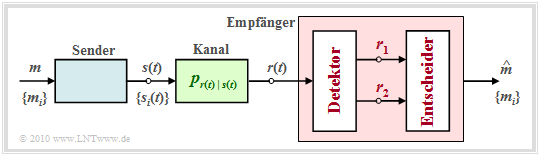
Um die Frage zu klären, welche und wieviele Messungen am Empfangssignal $r(t)$ durchzuführen sind, um Optimalität zu garantieren, ist das Theorem der Irrelevanz hilfreich. Dazu betrachten wir den skizzierten Empfänger, dessen Detektor aus dem Empfangssignal $r(t)$ die zwei Vektoren $\boldsymbol{r}_1$ und $\boldsymbol{r}_2$ ableitet und dem Entscheider zur Verfügung stellt. Diese Größen stehen mit der Nachricht $ m \in \{m_i\}$ über die Verbundwahrscheinlichkeitsdichte $p_{\boldsymbol{ r}_1, \hspace{0.05cm}\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm}m }$ in Zusammenhang.
Die Entscheidungsregel des MAP–Empfängers lautet mit Anpassung an dieses Beispiel:
- $$\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 , \hspace{0.05cm}\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1, \hspace{0.05cm}\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} m_i ) \big]= {\rm arg} \max_i \hspace{0.1cm}\big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )\big] \hspace{0.05cm}.$$
Hierzu ist anzumerken:
- Die Vektoren $\boldsymbol{r}_1$ und $\boldsymbol{r}_2$ sind Zufallsgrößen. Ihre Realisierungen werden hier und im Folgenden mit $\boldsymbol{\rho}_1$ und $\boldsymbol{\rho}_2$ bezeichnet. Zur Hervorhebung sind alle Vektoren in der Grafik rot eingetragen.
- Die Voraussetzungen für die Anwendung des „Theorems der Irrelevanz” sind die gleichen wie die an eine Markovkette erster Ordnung. Die Zufallsvariablen $x$, $y$, $z$ formen dann eine Markovkette erster Ordnung, falls die Verteilung von $z$ bei gegebenem $y$ unabhängig von $x$ ist:
- $$p(x, y, z) = p(x) \cdot p(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot p(z\hspace{0.05cm} \vert \hspace{0.05cm}y) \hspace{0.25cm} {\rm anstelle \hspace{0.15cm}von} \hspace{0.25cm}p(x, y, z) = p(x) \cdot p(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot p(z\hspace{0.05cm} \vert \hspace{0.05cm}x, y) \hspace{0.05cm}.$$
- Der optimale Empfänger muss im allgemeinen Fall beide Vektoren $\boldsymbol{r}_1$ und $\boldsymbol{r}_2$ auswerten, da in obiger Entscheidungsregel beide Verbundwahrscheinlichkeitsdichten $p_{\boldsymbol{ r}_1\hspace{0.05cm} \vert \hspace{0.05cm}m }$ und $p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r}_1, \hspace{0.05cm}m }$ auftreten.
- Dagegen kann der Empfänger ohne Informationseinbuße die zweite Messung vernachlässigen, falls $\boldsymbol{r}_2$ bei gegebenem $\boldsymbol{r}_1$ unabhängig von der Nachricht $m$ ist:
- $$p_{\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 ) \hspace{0.05cm}.$$
- In diesem Fall lässt sich die Entscheidungsregel weiter vereinfachen:
- $$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) \big]$$
- $$\Rightarrow \hspace{0.3cm}\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 )\big]$$
- $$\Rightarrow \hspace{0.3cm}\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \big]\hspace{0.05cm}.$$
$\text{Beispiel 1:}$ Betrachten wir zur Verdeutlichung des soeben vorgestellten Theorems der Irrelevanz zwei verschiedene Systemkonfigurationen mit jeweils zwei Rauschtermen $\boldsymbol{ n}_1$ und $\boldsymbol{ n}_1$. In der Grafik sind alle vektoriellen Größen rot eingezeichnet . Die Größen und $\boldsymbol{s}$, $\boldsymbol{ n}_1$ und $\boldsymbol{ n}_1$seien jeweils unabhängig voneinander.
Die Analyse dieser beiden Anordnungen liefert folgende Ergebnisse:
- Der Entscheider muss in beiden Fällen die Komponente $\boldsymbol{ r}_1= \boldsymbol{ s}_i + \boldsymbol{ n}_1$ berücksichtigen, da nur diese die Information über das Nutzsignal $\boldsymbol{ s}_i$ und damit über die gesendete Nachricht $m_i$ liefert.
- Bei der oberen Konfiguration enthält $\boldsymbol{ r}_2$ keine Information über $m_i$, die nicht bereits von $\boldsymbol{ r}_1$ geliefert wurde. Vielmehr ist $\boldsymbol{ r}_2= \boldsymbol{ r}_1 + \boldsymbol{ n}_2$ nur eine verrauschte Version von $\boldsymbol{ r}_1$ und hängt nur vom Rauschen $\boldsymbol{ n}_2$ ab, sobald $\boldsymbol{ r}_1$ bekannt ist ⇒ $\boldsymbol{ r}_2$ ist irrelevant:
- $$p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}_1 )= p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2 - \boldsymbol{\rho}_1 )\hspace{0.05cm}.$$
- Bei der unteren Konfiguration ist dagegen $\boldsymbol{ r}_2= \boldsymbol{ n}_1 + \boldsymbol{ n}_2$ für den Empfänger hilfreich, da ihm so ein Schätzwert für den Rauschterm $\boldsymbol{ n}_1$ geliefert wird ⇒ $\boldsymbol{ r}_2$ sollte deshalb hier nicht verworfen werden. Formal lässt sich dieses Resultat wie folgt ausdrücken:
- $$p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) = p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i)= p_{\boldsymbol{ n}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i) = p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i ) \hspace{0.05cm}.$$
- Da nun im Argument dieser Funktion die Nachricht $\boldsymbol{ s}_i$ erscheint, ist $\boldsymbol{ r}_2$ „nicht irrelevant”, sondern durchaus relevant.
Einige Eigenschaften des AWGN-Kanals
Um weitere Aussagen über die Art der optimalen Messungen des Vektors $\boldsymbol{ r}$ machen zu können, ist es notwendig, die den Kanal charakterisierende (bedingte) Wahrscheinlichkeitsdichtefunktion $p_{\hspace{0.02cm}r(t)\hspace{0.05cm} \vert \hspace{0.05cm}s(t)}$ weiter zu spezifizieren. Im Folgenden wird die Kommunikation über den AWGN–Kanal betrachtet, dessen wichtigste Eigenschaften hier nochmals kurz zusammengestellt werden:
- Das Ausgangssignal des AWGN–Kanals ist $r(t) = s(t)+n(t)$, wobei $s(t)$ das Sendesignal angibt und $n(t)$ durch einen Gaußschen Rauschprozess dargestellt wird.
- Ein Zufallsprozess $\{n(t)\}$ ist gaußisch, falls die Elemente der $k$–dimensionalen Zufallsvariablen $\{n_1(t)\hspace{0.05cm} \text{...} \hspace{0.05cm}n_k(t)\}$ gemeinsam gaußverteilt sind ⇒ „Jointly Gaussian”.
- Der Mittelwert des AWGN–Rauschens ist ${\rm E}\big[n(t)\big] = 0$. Außerdem ist $n(t)$ „weiß”, was bedeutet, dass das Leistungsdichtespektrum (LDS) für alle Frequenzen (von $-\infty$ bis $+\infty$) konstant ist: ${\it \Phi_n(f)} = {N_0}/{2} \hspace{0.05cm}.$
- Nach dem Wiener–Chintchine–Theorem ergibt sich die Autokorrelationsfunktion (AKF) als die Fourierrücktransformierte von ${\it \Phi_n(f)}$:
- $${\varphi_n(\tau)} = {\rm E}\big [n(t) \cdot n(t+\tau)\big ] = {N_0}/{2} \cdot \delta(t)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm E}\big [n(t) \cdot n(t+\tau)\big ] = \left\{ \begin{array}{c} \rightarrow \infty \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f{\rm \ddot{u}r}} \hspace{0.15cm} \tau = 0 \hspace{0.05cm}, \\ {\rm f{\rm \ddot{u}r}} \hspace{0.15cm} \tau \ne 0 \hspace{0.05cm},\\ \end{array}$$
- $N_0$ gibt dabei die physikalische (nur für $f \ge 0$ definierte) Rauschleistungsdichte an. Der konstante LDS–Wert $(N_0/2)$ und das Gewicht der Diracfunktion in der AKF (ebenfalls $N_0/2$) ergibt sich allein durch die zweiseitige Betrachtungsweise.
Weitere Informationen zum AWGN–Kanal liefert das Lernvideo Der AWGN-Kanal im Teil 2.
Beschreibung des AWGN-Kanals durch orthonormale Basisfunktionen
Aus dem vorletzten Statement auf der letzten Seite geht hervor, dass
- reines AWGN–Rauschen $n(t)$ stets eine unendliche Varianz (Leistung) aufweist: $\sigma_n^2 \to \infty$,
- in der Realität demzufolge nur gefiltertes Rauschen $n\hspace{0.05cm}'(t) = n(t) \star h_n(t)$ auftreten kann.
Mit der Impulsantwort $h_n(t)$ und dem Frequenzgang $H_n(f) = {\rm F}\big [h_n(t)\big ]$ gelten dann folgende Gleichungen:
- $${\rm E}\big[n\hspace{0.05cm}'(t) \big] \hspace{0.15cm} = \hspace{0.2cm} {\rm E}\big[n(t) \big] = 0 \hspace{0.05cm},$$
- $${\it \Phi_{n\hspace{0.05cm}'}(f)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2} \cdot |H_{n}(f)|^2 \hspace{0.05cm},$$
- $$ {\it \varphi_{n\hspace{0.05cm}'}(\tau)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2}\hspace{0.1cm} \cdot \big [h_{n}(\tau) \star h_{n}(-\tau)\big ]\hspace{0.05cm},$$
- $$\sigma_n^2 \hspace{0.1cm} = \hspace{0.1cm} { \varphi_{n\hspace{0.05cm}'}(\tau = 0)} = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}h_n^2(t)\,{\rm d} t ={N_0}/{2}\hspace{0.1cm} \cdot < \hspace{-0.1cm}h_n(t), \hspace{0.1cm} h_n(t) \hspace{-0.05cm} > \hspace{0.1cm} = \int_{-\infty}^{+\infty}{\it \Phi_{n\hspace{0.05cm}'}(f)}\,{\rm d} f = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|H_n(f)|^2\,{\rm d} f \hspace{0.05cm}.$$
Im Folgenden beinhaltet $n(t)$ stets implizit eine Bandbegrenzung; auf die Schreibweise $n'(t)$ wird also zukünftig verzichtet.
$\text{Bitte beachten Sie:}$ Ähnlich wie das Sendesignal $s(t)$ lässt sich auch der Rauschprozess $\{n(t)\}$ als gewichtete Summe von orthonormalen Basisfunktionen $\varphi_j(t)$ schreiben.
- Im Gegensatz zu $s(t)$ ist allerdings nun eine Beschränkung auf eine endliche Anzahl an Basisfunktionen nicht möglich.
- Vielmehr gilt bei rein stochastischen Größen für die entsprechende Signaldarstellung
- $$n(t) = \lim_{N \rightarrow \infty} \sum\limits_{j = 1}^{N}n_j \cdot \varphi_j(t) \hspace{0.05cm},$$
wobei der Koeffizient $n_j$ durch die Projektion von $n(t)$ auf die Basisfunktion $\varphi_j(t)$ bestimmt ist:
- $$n_j = \hspace{0.1cm} < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.05cm}.$$
Hinweis: Um eine Verwechslung mit den Basisfunktionen $\varphi_j(t)$ zu vermeiden, wird im Folgenden die AKF $\varphi_n(\tau)$ des Rauschprozesses stets nur noch als der Erwartungswert ${\rm E}\big [n(t) \cdot n(t + \tau)\big ]$ ausgedrückt.
Optimaler Empfänger für den AWGN-Kanal
Auch das Empfangssignal $r(t) = s(t) + n(t)$ lässt sich in bekannter Weise in Basisfunktionen zerlegen:
- $$r(t) = \sum\limits_{j = 1}^{\infty}r_j \cdot \varphi_j(t) \hspace{0.05cm}.$$
Zu berücksichtigen ist:
- Die $M$ möglichen Sendesignale $\{s_i(t)\}$ spannen einen Signalraum mit insgesamt $N$ Basisfunktionen $\varphi_1(t)$, ... , $\varphi_N(t)$ auf.
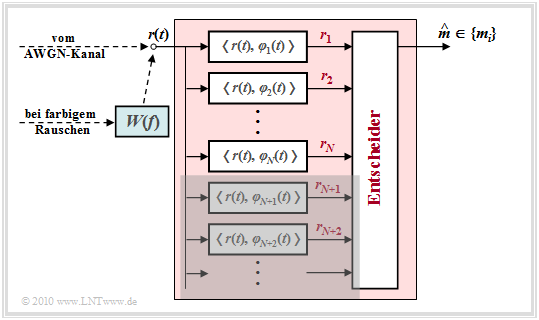
- Diese $N$ Basisfunktionen $\varphi_j(t)$ werden gleichzeitig zur Beschreibung des Rauschsignals $n(t)$ und des Empfangssignals $r(t)$ verwendet.
- Zur vollständigen Charakterisierung von $n(t)$ bzw. $r(t)$ werden nun aber darüber hinaus noch unendlich viele weitere Basisfunktionen $\varphi_{N+1}(t)$, $\varphi_{N+2}(t)$, ... benötigt.
Damit ergeben sich die Koeffizienten des Empfangssignals $r(t)$ gemäß folgender Gleichung, wobei berücksichtigt ist, dass die Signale $s_i(t)$ und das Rauschen $n(t)$ voneinander unabhängig sind:
- $$r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}=\hspace{0.1cm} \left\{ \begin{array}{c} < \hspace{-0.1cm}s_i(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > + < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}= s_{ij}+ n_j\\ < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm} = n_j \end{array} \right.\quad \begin{array}{*{1}c} {j = 1, 2, \hspace{0.05cm}\text{...}\hspace{0.05cm} \hspace{0.05cm}, N} \hspace{0.05cm}, \\ {j > N} \hspace{0.05cm}.\\ \end{array}$$
Somit ergibt sich für den optimalen Empfänger die oben skizzierte Struktur.
Betrachten wir zunächst den AWGN–Kanal. Hier kann auf das Vorfilter mit dem Frequenzgang $W(f)$ verzichtet werden, das für farbiges Rauschen vorgesehen ist.
Der Detektor des optimalen Empfängers bildet die Koeffizienten $r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t)\hspace{-0.05cm} >$ und reicht diese an den Entscheider weiter. Basiert die Entscheidung auf sämtlichen – also unendlich vielen – Koeffizienten $r_j$, so ist die Wahrscheinlichkeit für eine Fehlentscheidung minimal und der Empfänger optimal.
Die reellwertigen Koeffizienten $r_j$ wurden oben wie folgt berechnet:
- $$r_j = \left\{ \begin{array}{c} s_{ij} + n_j\\ n_j \end{array} \right.\quad \begin{array}{*{1}c} {j = 1, 2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, N} \hspace{0.05cm}, \\ {j > N} \hspace{0.05cm}.\\ \end{array}$$
Nach dem Theorem der Irrelevanz lässt sich zeigen, dass für additives weißes Gaußsches Rauschen
- die Optimalität nicht herabgesetzt wird, wenn man die nicht von der Nachricht $(s_{ij})$ abhängigen Koeffizienten $r_{N+1}$, $r_{N+2}$, ... nicht in den Entscheidungsprozess einbindet, und somit
- der Detektor nur die Projektionen des Empfangssignals $r(t)$ auf die $N$ durch das Nutzsignal $s(t)$ vorgegebenen Basisfunktionen $\varphi_{1}(t)$, ... , $\varphi_{N}(t)$ bilden muss.
In der Grafik ist diese signifikante Vereinfachung durch die graue Hinterlegung angedeutet.
Im Fall von farbigem Rauschen ⇒ Leistungsdichtespektrum ${\it \Phi_n(f)} \ne {\rm const.}$ ist lediglich zusätzlich ein Vorfilter mit dem Amplitudengang $|W(f)| = {1}/{\sqrt{\it \Phi_n(f)}}$ erforderlich. Man nennt dieses Filter auch „Whitening Filter”, da die Rauschleistungsdichte am Ausgang wieder konstant, also „weiß” ist. Genaueres hierzu finden Sie im Kapitel Matched-Filter bei farbigen Störungen des Buches „Stochastische Signaltheorie”.
Implementierungsaspekte
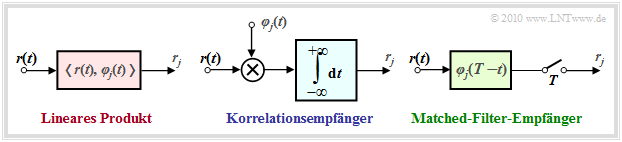
Wesentliche Bestandteile des optimalen Empfängers sind die Berechnungen der inneren Produkte gemäß den Gleichungen $r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} >$. Diese können auf verschiedene Art und Weise implementiert werden:
- Beim Korrelationsempfänger (Näheres zu dieser Implementierung finden Sie im gleichnamigen Kapitel) werden die inneren Produkte direkt entsprechend der Definition mit analogen Multiplizierern und Integratoren realisiert:
- $$r_j = \int_{-\infty}^{+\infty}r(t) \cdot \varphi_j(t) \,{\rm d} t \hspace{0.05cm}.$$
- Der Matched–Filter–Empfänger, der bereits im Kapitel Optimaler Binärempfänger zu Beginn dieses Buches hergeleitet wurde, erzielt mit einem linearen Filter mit der Impulsantwort $h_j(t) = \varphi_j(t) \cdot (T-t)$ und anschließender Abtastung zum Zeitpunkt $t = T$ das gleiche Ergebnis:
- $$r_j = \int_{-\infty}^{+\infty}r(\tau) \cdot h_j(t-\tau) \,{\rm d} \tau = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(T-t+\tau) \,{\rm d} \tau \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_j (t = \tau) = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(\tau) \,{\rm d} \tau = r_j \hspace{0.05cm}.$$
Die Abbildung zeigt die beiden möglichen Realisierungsformen des optimalen Detektors.
Wahrscheinlichkeitsdichtefunktion der Empfangswerte
Bevor wir uns im folgenden Kapitel der optimalen Gestaltung des Entscheiders und der Berechnung und Annäherung der Fehlerwahrscheinlichkeit zuwenden, erfolgt zunächst eine für den AWGN–Kanal gültige statistische Analyse der Entscheidungsgrößen $r_j$.
Dazu betrachten wir nochmals den optimalen Binärempfänger für die bipolare Basisbandübertragung über den AWGN–Kanal, wobei wir von der für das vierte Hauptkapitel gültigen Beschreibungsform ausgehen.
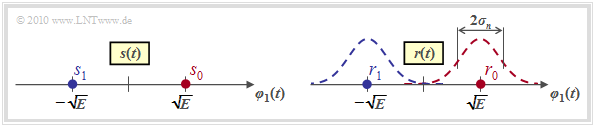
Mit den Parametern $N = 1$ und $M = 2$ ergibt sich für das Sendesignal die in der linken Grafik dargestellte Signalraumkonstellation
- mit nur einer Basisfunktion $\varphi_1(t)$, wegen $N = 1$,
- mit den beiden Signalraumpunkten $s_i \in \{s_0, \hspace{0.05cm}s_1\}$, wegen $M = 2$.
Für das Signal $r(t) = s(t) + n(t)$ am Ausgang des AWGN–Kanals ergibt sich im rauschfreien Fall ⇒ $r(t) = s(t)$ die genau gleiche Konstellation. Die Signalraumpunkte liegen somit bei
- $$r_0 = s_0 = \sqrt{E}\hspace{0.05cm},\hspace{0.2cm}r_1 = s_1 = -\sqrt{E}\hspace{0.05cm}.$$
Bei Berücksichtigung des (bandbegrenzten) AWGN–Rauschens $n(t)$ überlagern sich den beiden Punkten $r_0$ und $r_1$ jeweils Gaußkurven mit der Varianz $\sigma_n^2$ ⇒ Streuung $\sigma_n$ (siehe rechte Grafik). Die WDF der Rauschkomponente $n(t)$ lautet dabei:
- $$p_n(n) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm e}^{ - {n^2}/(2 \sigma_n^2)}\hspace{0.05cm}.$$
Für die bedingte Wahrscheinlichkeitsdichte, dass der Empfangswert $\rho$ anliegt, wenn $s_i$ gesendet wurde, ergibt sich dann folgender Ausdruck:
- $$p_{\hspace{0.02cm}r\hspace{0.05cm}|\hspace{0.05cm}s}(\rho\hspace{0.05cm}|\hspace{0.05cm}s_i) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm e}^{ - {(\rho - s_i)^2}/(2 \sigma_n^2)} \hspace{0.05cm}.$$
Zu den Einheiten der hier aufgeführten Größen ist zu bemerken:
- $r_0 = s_0$ und $r_1 = s_1$ sowie $n$ sind jeweils Skalare mit der Einheit „Wurzel aus Energie”.
- Damit ist offensichtlich, dass $\sigma_n$ ebenfalls die Einheit „Wurzel aus Energie” besitzt und $\sigma_n^2$ eine Energie darstellt.
- Beim AWGN–Kanal ist die Rauschvarianz $\sigma_n^2 = N_0/2$. Diese ist also ebenfalls eine physikalische Größe mit der Einheit $\rm W/Hz = Ws$.
Die hier angesprochene Thematik wird in der Aufgabe 4.6 an Beispielen verdeutlicht.
N–dimensionales Gaußsches Rauschen
Liegt ein $N$–dimensionales Modulationsverfahren vor, das heißt, es gilt mit $0 \le i \le M-1$ und $1 \le j \le N$:
- $$s_i(t) = \sum\limits_{j = 1}^{N} s_{ij} \cdot \varphi_j(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + \hspace{0.05cm}\text{...}\hspace{0.05cm} + s_{iN} \cdot \varphi_N(t)\hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \boldsymbol{ s}_i = \left(s_{i1}, s_{i2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, s_{iN}\right ) \hspace{0.05cm},$$
so muss der Rauschvektor $\boldsymbol{ n}$ ebenfalls mit der Dimension $N$ angesetzt werden. Das gleiche gilt auch für den Empfangsvektor $\boldsymbol{ r}$:
- $$\boldsymbol{ n} = \left(n_{1}, n_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, n_{N}\right ) \hspace{0.01cm},\hspace{0.2cm}\boldsymbol{ r} = \left(r_{1}, r_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, r_{N}\right )\hspace{0.05cm}.$$
Die Wahrscheinlichkeitsdichtefunktion (WDF) lautet dann für den AWGN–Kanal mit der Realisierung $\boldsymbol{ \eta}$ des Rauschsignals
- $$p_{\boldsymbol{ n}}(\boldsymbol{ \eta}) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^N } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \eta} ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm},$$
und für die bedingte WDF in der Maximum–Likelihood–Entscheidungsregel ist anzusetzen:
- $$p_{\hspace{0.02cm}\boldsymbol{ r}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_i) \hspace{-0.1cm} = \hspace{0.1cm} p_{\hspace{0.02cm} \boldsymbol{ n}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} - \boldsymbol{ s}_i \hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}_i) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \rho} - \boldsymbol{ s}_i ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.$$
Die Gleichung ergibt sich aus der allgemeinen Darstellung der $N$–dimensionalen Gaußschen WDF im Abschnitt Korrelationsmatrix des Buches „Stochastische Signaltheorie” unter der Voraussetzung, dass die Komponenten unkorreliert (und somit statistisch unabhängig) sind. $||\boldsymbol{ \eta}||$ bezeichnet man als die Norm (Länge) des Vektors $\boldsymbol{ \eta}$.
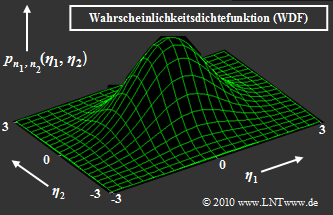
$\text{Beispiel 2:}$ Rechts dargestellt ist die zweidimensionale Gauß–WDF $p_{\boldsymbol{ n} } (\boldsymbol{ \eta})$ der 2D–Zufallsgröße $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$. Beliebige Realisierungen der Zufallsgröße $\boldsymbol{ n}$ werden mit $\boldsymbol{ \eta} = (\eta_1,\hspace{0.05cm}\eta_2)$ bezeichnet.
- Die Gleichung der dargestellten Glockenkurve lautet:
- $$p_{n_1, n_2}(\eta_1, \eta_2) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot {\rm exp} \left [ - \frac{ \eta_1^2 + \eta_2^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}. $$
- Das Maximum dieser Funktion liegt bei $\eta_1 = \eta_2 = 0$ und hat den Wert $2\pi \cdot \sigma_n^2$.
- Mit $\sigma_n^2 = N_0/2$ lässt sich die 2D–WDF in Vektorform auch wie folgt schreiben:
- $$p_{\boldsymbol{ n} }(\boldsymbol{ \eta}) = \frac{1}{\pi \cdot N_0 } \cdot {\rm exp} \left [ - \frac{\vert \vert \boldsymbol{ \eta} \vert \vert ^2}{N_0}\right ]\hspace{0.05cm}.$$
- Diese rotationssymmetrische WDF eignet sich zum Beispiel für die Beschreibung/Untersuchung eines zweidimensionalen Modulationsverfahrens wie M–QAM, M–PSK oder 2–FSK.
- Oft werden zweidimensionale reelle Zufallsgrößen aber auch eindimensional–komplex dargestellt, meist in der Form $n(t) = n_{\rm I}(t) + {\rm j} \cdot n_{\rm Q}(t)$ Die beiden Komponenten bezeichnet man dann als Inphaseanteil $n_{\rm I}(t)$ und Quadraturanteil $n_{\rm Q}(t)$ des Rauschens.
- Die Wahrscheinlichkeitsdichtefunktion hängt nur vom Betrag $\vert n(t) \vert$ der Rauschvariablen ab und nicht von Winkel ${\rm arc} \ n(t)$. Das heißt: Komplexes Rauschen ist zirkulär symmetrisch (siehe Grafik).
- Zirkulär symmetrisch bedeutet auch, dass Inphasekomponente $n_{\rm I}(t)$ und Quadraturkomponente $n_{\rm Q}(t)$ die gleiche Verteilung aufweisen und damit auch gleiche Varianz (Streuung) besitzen:
- $$ {\rm E} \big [ n_{\rm I}^2(t)\big ] = {\rm E}\big [ n_{\rm Q}^2(t)\big ] = {\rm E}\big [ n_{\rm Q}^2(t) \big ] = \sigma_n^2 \hspace{0.05cm},\hspace{1cm}{\rm E}\big [ n(t) \cdot n^*(t) \big ]\hspace{0.1cm} = \hspace{0.1cm} {\rm E}\big [ n_{\rm I}^2(t) \big ] + {\rm E}\big [ n_{\rm Q}^2(t)\big ] = 2\sigma_n^2 \hspace{0.05cm}.$$
Abschließend noch einige Bezeichnungsvarianten für Gaußsche Zufallsgrößen:
- $$x ={\cal N}(\mu, \sigma^2) \hspace{-0.1cm}: \hspace{0.3cm}\text{reelle gaußverteilte Zufallsgröße, mit Mittelwert}\hspace{0.1cm}\mu \text { und Varianz}\hspace{0.15cm}\sigma^2 \hspace{0.05cm},$$
- $$y={\cal CN}(\mu, \sigma^2)\hspace{-0.1cm}: \hspace{0.12cm}\text{komplexe gaußverteilte Zufallsgröße} \hspace{0.05cm}.$$
Aufgaben zum Kapitel
Aufgabe 4.4: Maximum–a–posteriori und Maximum–Likelihood
Aufgabe 4.5: Theorem der Irrelevanz