Aufgaben:Aufgabe 2.3: cos- und sin-Anteil: Unterschied zwischen den Versionen
K (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Zeile 6: | Zeile 6: | ||
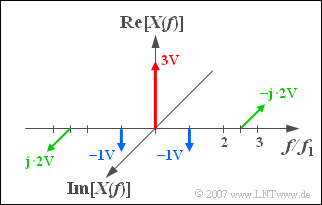
Gegeben ist das Amplitudenspektrum $X(f)$ eines Signals $x(t)$ entsprechend der Grafik. | Gegeben ist das Amplitudenspektrum $X(f)$ eines Signals $x(t)$ entsprechend der Grafik. | ||
| − | Die Normierungsfrequenz sei $f_1 = 4\,\text{kHz}$ . Damit liegen die tatsächlichen Frequenzen der Signalanteile bei $0\,\text{kHz}$, $4\,\text{kHz}$ und $10\,\text{kHz}$ . | + | *Die Normierungsfrequenz sei $f_1 = 4\,\text{kHz}$. |
| + | *Damit liegen die tatsächlichen Frequenzen der Signalanteile bei $0\,\text{kHz}$, $4\,\text{kHz}$ und $10\,\text{kHz}$ . | ||
| + | |||
Dieses Signal $x(t)$ liegt am Eingang eines linearen Differenzierers, dessen Ausgang mit $\omega_1 = 2\pi f_1$ wie folgt dargestellt werden kann: | Dieses Signal $x(t)$ liegt am Eingang eines linearen Differenzierers, dessen Ausgang mit $\omega_1 = 2\pi f_1$ wie folgt dargestellt werden kann: | ||
| − | :$$y(t)=\frac{1}{\omega_1}\cdot\frac{\rm d | + | :$$y(t)=\frac{1}{\omega_1}\cdot\frac{ {\rm d} x(t)}{{\rm d} t}.$$ |
| − | '' | + | ''Hinweis:'' |
*Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Harmonische_Schwingung|Harmonische Schwingung]]. | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Harmonische_Schwingung|Harmonische Schwingung]]. | ||
| + | |||
| + | |||
| + | |||
| Zeile 41: | Zeile 46: | ||
+ $y(t)$ hat die gleiche Periodendauer wie das Signal $x(t)$. | + $y(t)$ hat die gleiche Periodendauer wie das Signal $x(t)$. | ||
- $Y(f)$ beinhaltet eine Diracfunktion bei der Frequenz $f = 0$. | - $Y(f)$ beinhaltet eine Diracfunktion bei der Frequenz $f = 0$. | ||
| − | - $Y(f)$ beinhaltet eine Diracfunktion bei $f_1$ mit Gewicht $\rm{j} · 1\,{\rm V}$. | + | - $Y(f)$ beinhaltet eine Diracfunktion bei $+f_1$ mit dem Gewicht $\rm{j} · 1\,{\rm V}$. |
| − | + $Y(f)$ beinhaltet eine Diracfunktion bei $–\hspace{-0.1cm}2.5 \cdot f_1$ mit Gewicht $5\,{\rm V}$. | + | + $Y(f)$ beinhaltet eine Diracfunktion bei $–\hspace{-0.1cm}2.5 \cdot f_1$ mit dem Gewicht $5\,{\rm V}$. |
| Zeile 49: | Zeile 54: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
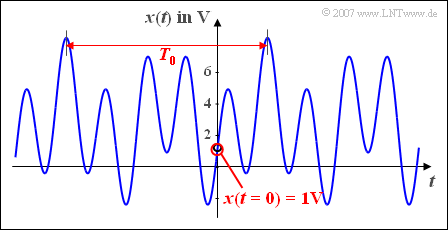
| + | [[Datei:P_ID293__Sig_A_2_3_a.png|right|frame|Summensignal aus Cosinus- und Sinusanteilen]] | ||
'''(1)''' Das Zeitsignal hat die folgende Form: | '''(1)''' Das Zeitsignal hat die folgende Form: | ||
:$$x(t)={\rm 3V}-{\rm 2V}\cdot \cos(\omega_{\rm 1} \cdot t)+{\rm 4V} \cdot \sin(2.5 \cdot \omega_{\rm 1} \cdot t).$$ | :$$x(t)={\rm 3V}-{\rm 2V}\cdot \cos(\omega_{\rm 1} \cdot t)+{\rm 4V} \cdot \sin(2.5 \cdot \omega_{\rm 1} \cdot t).$$ | ||
| − | Hierbei bezeichnet $\omega_1 = 2\pi f_1$ die Kreisfrequenz des Cosinusanteils. Zum Zeitpunkt $t = 0$ hat das Signal den Wert $\underline{1\,\rm V}$. | + | Hierbei bezeichnet $\omega_1 = 2\pi f_1$ die Kreisfrequenz des Cosinusanteils. Zum Zeitpunkt $t = 0$ hat das Signal den Wert $x(t=0)\hspace{0.15 cm}\underline{=1\,\rm V}$. |
| − | |||
| − | |||
'''(2)''' Die Grundfrequenz $f_0$ ist der kleinste gemeinsame Teiler | '''(2)''' Die Grundfrequenz $f_0$ ist der kleinste gemeinsame Teiler | ||
*von $f_1 = 4{\,\rm kHz}$ | *von $f_1 = 4{\,\rm kHz}$ | ||
| − | *und $2.5 · f_1 = 10{\,\rm kHz} | + | *und $2.5 · f_1 = 10{\,\rm kHz}$. |
| − | Daraus folgt $ | + | Daraus folgt $f_0 = 2{\,\rm kHz}$ ⇒ Periodendauer $T_0 = 1/f_0 \hspace{0.1cm}\underline{= 0.5 {\,\rm ms}}$. |
<br clear=all> | <br clear=all> | ||
[[Datei:P_ID294__Sig_A_2_3_d_neu.png|right|300px|frame|Spektrum mit diskreten Anteilen]] | [[Datei:P_ID294__Sig_A_2_3_d_neu.png|right|300px|frame|Spektrum mit diskreten Anteilen]] | ||
| Zeile 79: | Zeile 83: | ||
'''(4)''' Richtig sind die <u>Lösungsvorschläge 1 und 4</u>: | '''(4)''' Richtig sind die <u>Lösungsvorschläge 1 und 4</u>: | ||
| − | *Die Periodendauer $T_0$ wird durch die Amplitude und die Phase der beiden Anteile nicht verändert. Das bedeutet, dass weiterhin $T_0 = 0.5 {\,\rm ms}$ gilt. | + | *Die Periodendauer $T_0$ wird durch die Amplitude und die Phase der beiden Anteile nicht verändert. |
| + | *Das bedeutet, dass weiterhin $T_0 = 0.5 {\,\rm ms}$ gilt. | ||
*Der Gleichanteil verschwindet aufgrund der Differentiation. | *Der Gleichanteil verschwindet aufgrund der Differentiation. | ||
*Der Anteil bei $f_1$ ist sinusförmig. Somit hat $X(f)$ einen (imaginären) Dirac bei $f = f_1$, jedoch mit negativem Vorzeichen. | *Der Anteil bei $f_1$ ist sinusförmig. Somit hat $X(f)$ einen (imaginären) Dirac bei $f = f_1$, jedoch mit negativem Vorzeichen. | ||
Version vom 12. Juli 2018, 14:23 Uhr
Gegeben ist das Amplitudenspektrum $X(f)$ eines Signals $x(t)$ entsprechend der Grafik.
- Die Normierungsfrequenz sei $f_1 = 4\,\text{kHz}$.
- Damit liegen die tatsächlichen Frequenzen der Signalanteile bei $0\,\text{kHz}$, $4\,\text{kHz}$ und $10\,\text{kHz}$ .
Dieses Signal $x(t)$ liegt am Eingang eines linearen Differenzierers, dessen Ausgang mit $\omega_1 = 2\pi f_1$ wie folgt dargestellt werden kann:
- $$y(t)=\frac{1}{\omega_1}\cdot\frac{ {\rm d} x(t)}{{\rm d} t}.$$
Hinweis:
- Die Aufgabe gehört zum Kapitel Harmonische Schwingung.
Fragebogen
Musterlösung
(1) Das Zeitsignal hat die folgende Form:
- $$x(t)={\rm 3V}-{\rm 2V}\cdot \cos(\omega_{\rm 1} \cdot t)+{\rm 4V} \cdot \sin(2.5 \cdot \omega_{\rm 1} \cdot t).$$
Hierbei bezeichnet $\omega_1 = 2\pi f_1$ die Kreisfrequenz des Cosinusanteils. Zum Zeitpunkt $t = 0$ hat das Signal den Wert $x(t=0)\hspace{0.15 cm}\underline{=1\,\rm V}$.
(2) Die Grundfrequenz $f_0$ ist der kleinste gemeinsame Teiler
- von $f_1 = 4{\,\rm kHz}$
- und $2.5 · f_1 = 10{\,\rm kHz}$.
Daraus folgt $f_0 = 2{\,\rm kHz}$ ⇒ Periodendauer $T_0 = 1/f_0 \hspace{0.1cm}\underline{= 0.5 {\,\rm ms}}$.
(3) Für das Ausgangssignal $y(t)$ des Differenzierers gilt:
- $$y(t)=\frac{1}{\omega_1}\cdot\frac{ {\rm d}x(t)}{{\rm d}t}=\frac{ {\rm -2V}}{\omega_1}\cdot\omega_1 \cdot (-\sin(\omega_1 t))+\frac{\rm 4V}{\omega_1}\cdot 2.5\omega_1\cdot {\rm cos}(2.5\omega_1t).$$
Dies führt zum Ergebnis:
- $$y(t)={\rm 2V}\cdot\sin(\omega_1 t)+{\rm 10V}\cdot\cos(2.5\omega_1 t).$$
Für $t = 0$ ergibt sich der Wert $y(t=0)\hspace{0.15cm}\underline{=10\,\rm V}$. Rechts ist das Spektrum $Y(f)$ dargestellt.
(4) Richtig sind die Lösungsvorschläge 1 und 4:
- Die Periodendauer $T_0$ wird durch die Amplitude und die Phase der beiden Anteile nicht verändert.
- Das bedeutet, dass weiterhin $T_0 = 0.5 {\,\rm ms}$ gilt.
- Der Gleichanteil verschwindet aufgrund der Differentiation.
- Der Anteil bei $f_1$ ist sinusförmig. Somit hat $X(f)$ einen (imaginären) Dirac bei $f = f_1$, jedoch mit negativem Vorzeichen.
- Der Cosinusanteil mit der Amplitude ${10\,\rm V}$ hat die beiden Diracfunktionen bei $\pm 2.5 \cdot f_1$ zur Folge, jeweils mit dem Gewicht ${5\,\rm V}$ .