Aufgaben:Aufgabe 2.6: Zur Huffman-Codierung

• Zurück zum Buch

Baumdiagramm des
Huffman–Verfahrens

Wir betrachten hier eine Quellensymbolfolge $\langle q_\nu \rangle$ mit dem Symbolumfang $M = 8$:

$$q_{\nu} = \{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm}, \boldsymbol{\rm B}\hspace{0.05cm}, \boldsymbol{\rm C}\hspace{0.05cm}, \boldsymbol{\rm D}\hspace{0.05cm}, \boldsymbol{\rm E}\hspace{0.05cm}, \boldsymbol{\rm F}\hspace{0.05cm}, \boldsymbol{\rm G}\hspace{0.05cm}, \boldsymbol{\rm H}\hspace{0.05cm} \}\hspace{0.05cm}.$$

Sind die Symbole gleichwahrscheinlich, also gilt $p_{\rm A} = p_{\rm B} =$ ... $ = p_{\rm H} = 1/M$, so macht Quellencodierung keinen Sinn. Bereits mit dem Dualcode $\rm A$ → 000, $\rm B$ → 001, ... , $\rm H$ → 111, erreicht nämlich die mittlere Codewortlänge $L_{\rm M}$ ihre untere Schranke $H$ gemäß dem Quellencodierungstheorem ($H$ bezeichnet hierbei die Quellenentropie):

$$L_{\rm M,\hspace{0.08cm}min} = H = 3 \hspace{0.15cm}{\rm bit/Quellensymbol} \hspace{0.05cm}.$$

Die Symbolwahrscheinlichkeiten seien aber in dieser Aufgabe wie folgt gegeben:

$$p_{\rm A} \hspace{-0.05cm}= \hspace{-0.05cm} 0.04 \hspace{0.05cm},\hspace{0.1cm}p_{\rm B} \hspace{-0.05cm}= \hspace{-0.05cm} 0.08 \hspace{0.05cm},\hspace{0.1cm}p_{\rm C} \hspace{-0.05cm}= \hspace{-0.05cm} 0.14 \hspace{0.05cm},\hspace{0.1cm} p_{\rm D} \hspace{-0.05cm}= \hspace{-0.05cm} 0.25 \hspace{0.05cm},$$

$$p_{\rm E} \hspace{-0.05cm}= \hspace{-0.05cm} 0.24 \hspace{0.05cm},\hspace{0.1cm}p_{\rm F} \hspace{-0.05cm}= \hspace{-0.05cm} 0.12 \hspace{0.05cm},\hspace{0.1cm}p_{\rm G} \hspace{-0.05cm}= \hspace{-0.05cm} 0.10 \hspace{0.05cm},\hspace{0.1cm} p_{\rm H} \hspace{-0.05cm}= \hspace{-0.05cm} 0.03 \hspace{0.05cm}.$$

Es liegt hier also eine redundante Nachrichtenquelle vor, die man durch Huffman–Codierung komprimieren kann. Der Algorithmus wurde 1952 – also kurz nach Shannons bahnbrechenden Arbeiten zur Informationstheorie – von David Albert Huffman veröffentlicht und erlaubt die Konstruktion von optimalen präfixfreien Codes.

Der Algorithmus soll hier ohne Herleitung und Beweis angegeben werden, wobei wir uns auf Binärcodes beschränken   ⇒   die Codesymbolfolge besteht nur aus Nullen und Einsen:

(1)   Man ordne die Symbole nach fallenden Auftrittswahrscheinlichkeiten.

(2)   Man fasse die zwei unwahrscheinlichsten Symbole zu einem neuen Symbol zusammen.

(3)   Man wiederhole Schritt (1) und (2), bis nur zwei (zusammengefasste) Symbole übrig bleiben.

(4)   Die wahrscheinlichere Symbolmenge wird mit 1 binär codiert, die andere Menge mit 0.

(5)   Man ergänze schrittweise (von unten nach oben) die aufgespaltenen Teilcodes mit 1 bzw. 0.

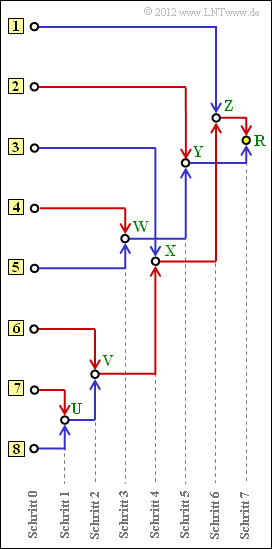
Oft wird dieser Algorithmus durch ein Baumdiagramm veranschaulicht. Die obige Grafik zeigt dieses für den vorliegenden Fall. Sie haben folgende Aufgaben:

(a)   Zuordnung der Symbole $\rm A$, ... , $\rm H$ zu den mit [1], ... , [8] bezeichneten Eingängen.

(b)   Bestimmung der Summenwahrscheinlichkeiten $U$, ... , $Z$ sowie $R$ (Root).

(c)   Zuordnung der Symbole $\rm A$, ... , $\rm H$ zu den entsprechenden Huffman–Binärfolgen. Eine rote Verbindung im Baumdiagramm entspricht einer 1 und eine blaue Verbindung einer 0.

Sie werden feststellen, dass die mittlere Codewortlänge

$$L_{\rm M} = \sum_{\mu = 1}^{M}\hspace{0.05cm} p_{\mu} \cdot L_{\mu} $$

bei Huffman–Codierung nur unwesentlich größer ist als die Quellenentropie $H$. In dieser Gleichung gelten für den vorliegenden Fall folgende Werte:

• $M = 8$, $p_1 = p_{\rm A}$, ... , $p_8 = p_{\rm H}$.
• Die jeweilige Bitanzahl der Codesymbole für $\rm A$, ... , $\rm H$ ist mit $L_1$, ... , $L_8$ bezeichnet.

Hinweise:

• Die Aufgabe gehört zum Kapitel Entropiecodierung nach Huffman.
• Insbesondere wird Bezug genommen auf die Seiten
  • Der Huffman-Algorithmus,
  • Darstellung des Huffman-Codes als Baumdiagramm.
• Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das Interaktionsmodul Shannon–Fano– und Huffman–Codierung.

Fragebogen

1

Welche Eingänge im Baumdiagramm stehen für

Eingangsnummer $ \ = \ $   ⇒   Symbol $\rm A$

Eingangsnummer $ \ = \ $   ⇒   Symbol $\rm B$

Eingangsnummer $ \ = \ $   ⇒   Symbol $\rm C$

Eingangsnummer $ \ = \ $   ⇒   Symbol $\rm D$

2

Welche Zahlenwerte (Wahrscheinlichkeiten sollten bei den Knoten im Baumdiagramm stehen?

Wahrscheinlichkeit $ \ = \ $   bei Knoten $\rm U$

Wahrscheinlichkeit $ \ = \ $   bei Knoten $\rm V$

Wahrscheinlichkeit $ \ = \ $   bei Knoten $\rm W$

Wahrscheinlichkeit $ \ = \ $   bei Knoten $\rm Z$

Wahrscheinlichkeit $ \ = \ $   bei $\rm Root$

3

Welche Binärcodes (darzustellen mit Nullen und Einsen) ergeben sich für

Binärcode $ \ = \ $   ⇒   Symbol $\rm A$

Binärcode $ \ = \ $   ⇒   Symbol $\rm B$

Binärcode $ \ = \ $   ⇒   Symbol $\rm C$

Binärcode $ \ = \ $   ⇒   Symbol $\rm D$

4

Wie groß ist die mittlere Codewortlänge?

$L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

5

Wie groß ist die Quellenentropie $H$? Hinweis: Es gibt genau eine Lösung.

	$H = 2.71\ \rm bit/Quellensymbol.$
	$H = 2.75\ \rm bit/Quellensymbol.$
	$H = 3.00\ \rm bit/Quellensymbol.$

Musterlösung

Musterlösung

(1)  Vor dem Huffman–Algorithmus müssen die Symbole nach ihren Auftrittswahrscheinlichkeiten sortiert werden. Da die zwei unwahrscheinlichsten Symbole schon im ersten Schritt zusammengefasst werden, nehmen die Auftrittswahrscheinlichkeiten von oben nach unten ab (in der unteren Grafik zu dieser Musterlösung von links nach rechts). Durch Vergleich mit dem Angabenblatt erhält man:

Symbol A: Eingang 7,     Symbol B: Eingang 6,     Symbol C: Eingang 3,     Symbol D: Eingang 1.

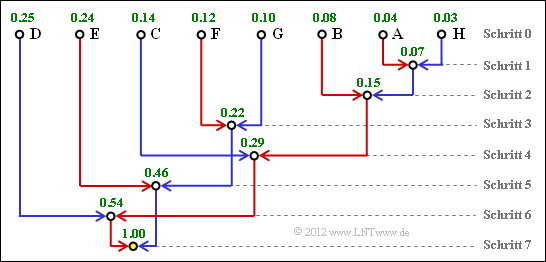
(2)  Der Knoten R ist die Baumwurzel (Root). Dieser ist stets mit R = 1 belegt, unabhängig von den Auftrittswahrscheinlichkeiten.

Für die weiteren Werte gilt:

Schritt 1:    U = p_A + p_H = 0.04 + 0.03 = 0.07,

Schritt 2:    V = U + p_B = 0.07 + 0.08 = 0.15,

Schritt 3:    W = p_F + p_G = 0.12 + 0.10 = 0.22,

Schritt 4:    X = V + p_C = 0.15 + 0.14 = 0.29,

Schritt 5:    Y = W + p_E = 0.22 + 0.24 = 0.46,

Schritt 6:    Z = X + p_D = 0.29 + 0.25 = 0.54.

Damit ergibt sich das hier dargestelle Baumdiagramm.

(3)  Den Huffman–Code für das Symbol A erhält man, wenn man den Weg von der Root (gelber Punkt) zum Symbol A zurückverfolgt und jeder roten Verbindungslinie eine „1” zuordnet, jeder blauen eine „0”.

• Symbol A:    rot–rot–rot–blau–rot → 11101,

• Symbol B:    rot–rot–rot–rot → 1111,

• Symbol C:    rot–rot–blau → 110,

• Symbol D:    rot–blau– → 10,

• Symbol E:    blau–rot → 01,

• Symbol F:    blau–blau–rot → 001,

• Symbol G:    blau–blau–blau → 000,

• Symbol H:    rot–rot–rot–blau–blau → 11100.

(4)  Die Codierung unter Punkt (3) hat ergeben, dass

• die Symbole D und E mit zwei Bit,

• die Symbole C, F und G mit drei Bit,

• das Symbol B mit vier Bit, und

• die Symbole A und H jeweils mit fünf Bit

dargestellt werden. Damit erhält man für die mittlere Codewortlänge (in „bit/Quellensymbol&dquo;):

$$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (p_{\rm D} + p_{\rm E}) \cdot 2 + (p_{\rm C} + p_{\rm F} + p_{\rm G}) \cdot 3 + p_{\rm B} \cdot 4 +(p_{\rm A} + p_{\rm H}) \cdot 5 = 0.49 \cdot 2 + 0.36 \cdot 3 +0.08 \cdot 4 +0.07 \cdot 5 \hspace{0.15cm}\underline{= 2.73}\hspace{0.05cm}.$$

(5)  Richtig ist allein Antwort 1:

• Die mittlere Codewortlänge L_M kann nicht kleiner sein als die Quellenentropie H. Damit scheiden die Antworten 2 und 3 aus.
• Aus den vorgegebenen Auftrittswahrscheinlichkeiten kann die Quellenentropie zu H = 2.71 bit/Quellensymbol berechnet werden.
• Man erkennt, dass die vorliegende Huffman–Codierung die durch das Quellencodierungstheorem vorgegebene Grenze L_{M, min} = H = 2.71 bit/Quellensymbol nahezu erreicht.