Aufgaben:Aufgabe 3.13: Coderate und Zuverlässigkeit: Unterschied zwischen den Versionen
| Zeile 58: | Zeile 58: | ||
+ $R′/C ≤ [1 + p_{\rm B} · \log_2 (p_{\rm B})]^{ –1 }$, | + $R′/C ≤ [1 + p_{\rm B} · \log_2 (p_{\rm B})]^{ –1 }$, | ||
+ $R′′/C ≤ 1 – p_{\rm B} · \log_2 (p_{\rm B})$, | + $R′′/C ≤ 1 – p_{\rm B} · \log_2 (p_{\rm B})$, | ||
| − | + $R′′′/C ≤ 1 + i · p_{\rm B}/ \lg(2)$ | + | + $R′′′/C ≤ 1 + i · p_{\rm B}/ \lg(2)$ für $p_{\rm B} = 10^{ –i}$. |
| Zeile 69: | Zeile 69: | ||
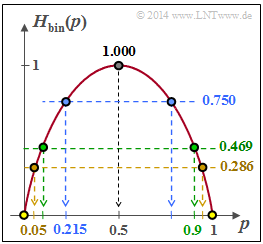
Aus der Grafik auf der Angabenseite (blaue Markierung) lässt sich ablesen: $ p_{\rm B,\hspace{0.05cm} min} \hspace{0.15cm} \underline {=0.215} \hspace{0.05cm}.$ | Aus der Grafik auf der Angabenseite (blaue Markierung) lässt sich ablesen: $ p_{\rm B,\hspace{0.05cm} min} \hspace{0.15cm} \underline {=0.215} \hspace{0.05cm}.$ | ||
| − | '''(2)''' Durch Umstellung obiger Gleichung erhält man mit $H_{bin}(p_B)$ aus der Grafik: | + | |
| + | '''(2)''' Durch Umstellung obiger Gleichung erhält man mit $H_{\rm bin}(p_B)$ aus der Grafik: | ||
:$$\begin{align*} R_{\rm max} = \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.10:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.469}\hspace{0.15cm} \underline {=0.942} \hspace{0.05cm},\\ | :$$\begin{align*} R_{\rm max} = \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.10:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.469}\hspace{0.15cm} \underline {=0.942} \hspace{0.05cm},\\ | ||
\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.05:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.286}\hspace{0.15cm} \underline {=0.700}\hspace{0.05cm}.\end{align*}$$ | \Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.05:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.286}\hspace{0.15cm} \underline {=0.700}\hspace{0.05cm}.\end{align*}$$ | ||
| + | |||
'''(3)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | '''(3)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | ||
| Zeile 79: | Zeile 81: | ||
*Die Differenz ist durch den zweiten Term der binären Entropiefunktion gegeben: | *Die Differenz ist durch den zweiten Term der binären Entropiefunktion gegeben: | ||
:$$ H_{\rm bin}( p) - p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} = (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ | :$$ H_{\rm bin}( p) - p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} = (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ | ||
| − | Dieser Term wird umso kleiner, je kleiner $p$ ist. Zutreffend ist also auch der <u>Lösungsvorschlag 3</u>, wie die folgenden Rechnungen zeigen: | + | *Dieser Term wird umso kleiner, je kleiner $p$ ist. |
| − | :$$ p_{\rm B} | + | *Zutreffend ist also auch der <u>Lösungsvorschlag 3</u>, wie die folgenden Rechnungen zeigen: |
| − | :$$p_{\rm B} | + | :$$ p_{\rm B} = 10^{-3}\text{:} \hspace{0.3cm} 0.999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.999}= 1.4420 \cdot 10^{-3} \hspace{0.05cm},$$ |
| − | :$$p_{\rm B | + | :$$p_{\rm B} = 10^{-4}\text{:} \hspace{0.3cm} 0.9999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9999}= 1.4427 \cdot 10^{-4} \hspace{0.05cm},$$ |
| + | :$$p_{\rm B} = 10^{-5}\text{:} \hspace{0.3cm} 0.99999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.99999}= 1.4427 \cdot 10^{-5} \hspace{0.05cm}.$$ | ||
| + | |||
'''(4)''' <u>Alle Lösungsvorschläge</u> sind zutreffend: | '''(4)''' <u>Alle Lösungsvorschläge</u> sind zutreffend: | ||
| − | *Der Ausdruck $R/C$ gibt die obere Schranke gemäß dem inversen Kanalcodierungstheorem an. Für $ | + | *Der Ausdruck $R/C$ gibt die obere Schranke gemäß dem inversen Kanalcodierungstheorem an. Für $p_{\rm B} = 10^{ –3 }$ erhält man folgende Schranke: |
| − | * Beim Vorschlag 2 ist die Näherung gemäß (3) berücksichtigt. Da nun der Nenner vergrößert wird, ist $R′/C < R/C$, beispielsweise gilt für $p_{\rm B} = 10{ –3 }\text{:}\hspace{0. | + | :$$R/C ≤ 1.01154 \hspace{0.5cm} ⇒ \hspace{0.5cm} R/C – 1 ≤ 1.154 · 10^{ –2 }.$$ |
| − | * Die Schranke $R′′ < R′$ ergibt sich, wenn man $1/(1 – ε)$ durch $1 + ε$ ersetzt ($ε$ ist positiv). Für $p_{\rm B} = 10^{–3}$ erhält man nun beispielsweise $R′′/C = 1.00997 | + | * Beim Vorschlag 2 ist die Näherung gemäß '''(3)''' berücksichtigt. Da nun der Nenner vergrößert wird, ist $R′/C < R/C$, beispielsweise gilt für |
| + | :$$p_{\rm B} = 10{ –3 }\text{:}\hspace{0.5cm} R′/C = 1.01007 · 10{ –2 }.$$ | ||
| + | : Es handelt sich auch hier um eine obere Schranke, etwas sicherer als die erste Schranke $R/C$. | ||
| + | * Die Schranke $R′′ < R′$ ergibt sich, wenn man $1/(1 – ε)$ durch $1 + ε$ ersetzt ($ε$ ist positiv). Für $p_{\rm B} = 10^{–3}$ erhält man nun beispielsweise | ||
| + | :$$R′′/C = 1.00997 \hspace{0.5cm} ⇒ \hspace{0.5cm} R′′/C – 1 ≤ 0.997 · 10^{–2}.$$ | ||
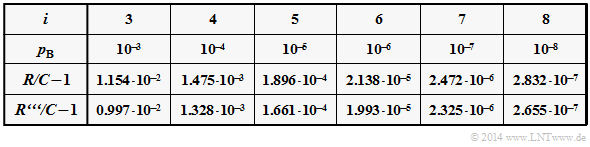
* $R′′′$ entsprechend dem letzten Vorschlag ist identisch mit $R′′$ und für Überschlagsrechnungen bei ganzzahligem Exponenten $i$ gut geeignet. Für den Zehnerlogarithmus gilt der Zahlenwert $\lg(2) ≈ 0.30103.$ | * $R′′′$ entsprechend dem letzten Vorschlag ist identisch mit $R′′$ und für Überschlagsrechnungen bei ganzzahligem Exponenten $i$ gut geeignet. Für den Zehnerlogarithmus gilt der Zahlenwert $\lg(2) ≈ 0.30103.$ | ||
| − | |||
| − | [[Datei:P_ID2806__Inf_A_3_12d.png|center|frame|Berechnete Schranken für die Coderaten]] | + | Die Tabelle zeigt für verschiedene Bitfehlerwahrscheinlichkeiten $p_{\rm B}$ die Abweichungen der ersten Schranke $(R/C-1)$ und der letzten Näherung $(R'''/C-1)$. Man erkennt die gute Übereinstimmung beider Schranken. |
| + | |||
| + | [[Datei:P_ID2806__Inf_A_3_12d.png|center|frame|Berechnete Schranken für die Coderaten; es gilt $p_{\rm B} = 10^{ –i}$]] | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 12. Oktober 2018, 14:00 Uhr
Das Kanalcodierungstheorem von Claude E. Shannon besagt unter anderem, dass über einen Kanal mit beliebig kleiner Blockfehlerwahrscheinlichkeit übertragen werden kann, so lange die Coderate $R$ nicht größer ist als die Kanalkapazität $C$. Dieses Ergebnis erreicht man mit Kanalcodierung (englisch: Channel Coding) allerdings nur bei sehr großen Blocklängen: $n → ∞$, was mit einem beliebig großen Aufwand verbunden ist.
Diese Aussage basiert auf informationstheoretischen Gesetzmäßigkeiten, die Shannon selbst aufgestellt hat. Shannon sagt nicht, wie diese „unendlich gute” Kanalcodierung aussehen muss, er beweist nur, dass es sie gibt.
Der Umkehrschluss des Kanalcodierungstheorems sagt aus, dass mit einer Rate $R > C$ keine fehlerfreie Übertragung möglich ist. Es gibt dann kein Codiersystem mit verschwindend kleiner Fehlerwahrscheinlichkeit, auch wenn die Codierung noch so aufwändig und ausgeklügelt wäre.
Vielmehr lassen sich für den Fall $R > C$ zwei Schranken angeben:
- Überträgt man über einen diskreten gedächtnislosen Kanal (DMC) mit einer Rate $R$ größer als die Kanalkapazität $C$, so gibt es eine untere Schranke für die Bitfehlerwahrscheinlichkeit:
- $$ p_{\rm B} \ge H_{\rm bin}^{-1} \left (1 - {C}/{R} \right) > 0 \hspace{0.05cm}.$$
- Soll die Bitfehlerwahrscheinlichkeit nach bestmöglicher Decodierung den Wert $p_{\rm B}$ nicht überschreiten, so darf die Rate einen gewissen Grenzwert nicht überschreiten:
- $$ R \le \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.05cm}.$$
In dieser Aufgabe sollen diese Gleichungen unter Verwendung der binären Entropiefunktion
- $$ H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}$$
numerisch ausgewertet werden.
- Diese ist oben skizziert.
- Wegen $0 < p_B ≤ 1$ und $0 < C/R < 1$ liegt das Argument der Funktion $H_{\rm bin}(⋅)$ und deren Umkehrfunktion $H_{\rm bin}^{ –1 }(⋅)$ stets zwischen $0$ und $1$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Anwendung auf die Digitalsignalübertragung.
- Bezug genommen wird insbesondere auf die Seite Rate, Kanalkapazität und Bitfehlerwahrscheinlichkeit.
- Die Werte der binären Entropiefunktion werden zum Beispiel durch das interaktice Berechnungsmodul Entropien von Nachrichtenquellen bereitgestellt.
Fragebogen
Musterlösung
- $$ p_{\rm B,\hspace{0.05cm} min} = H_{\rm bin}^{-1} \left (1 - \frac{C}{R} \right) = H_{\rm bin}^{-1} (0.75) \hspace{0.05cm}.$$
Aus der Grafik auf der Angabenseite (blaue Markierung) lässt sich ablesen: $ p_{\rm B,\hspace{0.05cm} min} \hspace{0.15cm} \underline {=0.215} \hspace{0.05cm}.$
(2) Durch Umstellung obiger Gleichung erhält man mit $H_{\rm bin}(p_B)$ aus der Grafik:
- $$\begin{align*} R_{\rm max} = \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.10:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.469}\hspace{0.15cm} \underline {=0.942} \hspace{0.05cm},\\ \Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.05:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.286}\hspace{0.15cm} \underline {=0.700}\hspace{0.05cm}.\end{align*}$$
(3) Richtig sind die Lösungsvorschläge 2 und 3:
- Für die binäre Entropiefunktion gilt definitionsgemäß:
- $$H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$
- Beide Terme sind positiv. Daraus folgt der Lösungsvorschlag 2: $H_{\rm bin}(p) = p · \log_2 \, (1/p)$.
- Die Differenz ist durch den zweiten Term der binären Entropiefunktion gegeben:
- $$ H_{\rm bin}( p) - p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} = (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$
- Dieser Term wird umso kleiner, je kleiner $p$ ist.
- Zutreffend ist also auch der Lösungsvorschlag 3, wie die folgenden Rechnungen zeigen:
- $$ p_{\rm B} = 10^{-3}\text{:} \hspace{0.3cm} 0.999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.999}= 1.4420 \cdot 10^{-3} \hspace{0.05cm},$$
- $$p_{\rm B} = 10^{-4}\text{:} \hspace{0.3cm} 0.9999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9999}= 1.4427 \cdot 10^{-4} \hspace{0.05cm},$$
- $$p_{\rm B} = 10^{-5}\text{:} \hspace{0.3cm} 0.99999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.99999}= 1.4427 \cdot 10^{-5} \hspace{0.05cm}.$$
(4) Alle Lösungsvorschläge sind zutreffend:
- Der Ausdruck $R/C$ gibt die obere Schranke gemäß dem inversen Kanalcodierungstheorem an. Für $p_{\rm B} = 10^{ –3 }$ erhält man folgende Schranke:
- $$R/C ≤ 1.01154 \hspace{0.5cm} ⇒ \hspace{0.5cm} R/C – 1 ≤ 1.154 · 10^{ –2 }.$$
- Beim Vorschlag 2 ist die Näherung gemäß (3) berücksichtigt. Da nun der Nenner vergrößert wird, ist $R′/C < R/C$, beispielsweise gilt für
- $$p_{\rm B} = 10{ –3 }\text{:}\hspace{0.5cm} R′/C = 1.01007 · 10{ –2 }.$$
- Es handelt sich auch hier um eine obere Schranke, etwas sicherer als die erste Schranke $R/C$.
- Die Schranke $R′′ < R′$ ergibt sich, wenn man $1/(1 – ε)$ durch $1 + ε$ ersetzt ($ε$ ist positiv). Für $p_{\rm B} = 10^{–3}$ erhält man nun beispielsweise
- $$R′′/C = 1.00997 \hspace{0.5cm} ⇒ \hspace{0.5cm} R′′/C – 1 ≤ 0.997 · 10^{–2}.$$
- $R′′′$ entsprechend dem letzten Vorschlag ist identisch mit $R′′$ und für Überschlagsrechnungen bei ganzzahligem Exponenten $i$ gut geeignet. Für den Zehnerlogarithmus gilt der Zahlenwert $\lg(2) ≈ 0.30103.$
Die Tabelle zeigt für verschiedene Bitfehlerwahrscheinlichkeiten $p_{\rm B}$ die Abweichungen der ersten Schranke $(R/C-1)$ und der letzten Näherung $(R'''/C-1)$. Man erkennt die gute Übereinstimmung beider Schranken.