Aufgaben:Aufgabe 2.6: Zweiwegekanal

• Zurück zum Buch

Impulsantwort des Zweiwegekanals

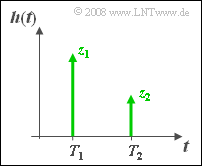
Der so genannte Zweiwegekanal wird durch folgende Impulsantwort charakterisiert (mit $T_1 < T_2$):

$$h(t) = z_1 \cdot \delta ( t - T_1) + z_2 \cdot \delta ( t - T_2).$$

• Bis auf wenige Kombinationen der Systemparameter $z_1$, $T_1$, $z_2$ und $T_2$ wird dieser Kanal zu linearen Verzerrungen führen.
• Man spricht nur dann von einem verzerrungsfreien Kanal, wenn durch ihn kein einziges Eingangssignal verzerrt wird. Das bedeutet:   Auch bei verzerrendem Kanal kann es Sonderfälle geben, bei denen tatsächlich $y(t) = \alpha \cdot x(t - \tau)$ gilt.

Als Testsignale werden an den Systemeingang angelegt:

• ein Diracpuls $x_1(t)$ im Zeitabstand $T_0 = 1 \ \rm ms$, dessen Spektralfunktion ebenfalls ein Diracpuls ist, und zwar mit Abstand $f_0 = 1/T_0 = 1 \ \rm kHz$:

$$x_1(t) = \sum_{n = - \infty}^{+\infty} \delta ( t - n \cdot T_0) ,\hspace{0.5cm} X_1(f) = T_0 \cdot \sum_{k = - \infty}^{+\infty} \delta ( f - k \cdot f_0) ,$$

• ein Cosinussignal mit der Frequenz $f_2 = 250 \ \rm Hz$:

$$x_2(t) = \cos(2 \pi \cdot f_2 \cdot t) ,$$

• die Summe zweier Cosinussignale mit den Frequenzen $f_2 = 250 \ \rm Hz$ und $f_3 = 1250 \ \rm Hz$:

$$x_3(t) = \cos(2 \pi \cdot f_2 \cdot t) + \cos(2 \pi \cdot f_3 \cdot t) .$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Lineare Verzerrungen.

• Um Ihnen einige Rechnungen zu ersparen, wird das Ergebnis für den Parametersatz $z_1 = 1$, $T_1 = 0$, $z_2 =0.5$, $T_2 = 1 \ \rm ms$ angegeben:

$$|H(f = f_2)| = |H(f = f_3)| = \sqrt{1.25} \approx 1.118, \; \; \; \; b(f = f_2) = b(f = f_3) = \arctan (0.5) \approx 0.464.$$

Fragebogen

1

Welche der folgenden Aussagen sind zutreffend?

	Der Parametersatz $\big[z_1 = 1$, $T_1 = 0$, $z_2 =0 \big]$ ist der einzig mögliche zur Beschreibung des idealen Kanals.
	Jeder verzerrungsfreie Kanal wird durch die beiden Kombinationen $\big[z_1 \ne 0, \; z_2 = 0 \big]$ bzw. $\big[z_1 = 0, \; z_2 \ne 0 \big]$ erfasst.
	Die Werte $\big[z_1 \ne 0\big]$ und $\big[z_2 \ne 0\big]$ führen zu einem verzerrungsfreien Kanal, wenn $T_1$ und $T_2$ bestmöglich angepasst sind.

2

Es gelte $z_1 = 1$,   $T_1 = 0$,  $z_2 =0.5$ und $T_2 = 1 \ \rm ms$. Berechnen Sie den Frequenzgang $H(f)$ dieses Kanals.
Welche Werte gibt es bei Vielfachen von $1 \ \rm kHz$?

${\rm Re}\big[H(f = n \cdot 1 \ {\rm kHz})\big] \ = \ $

${\rm Im}\big[H(f = n \cdot 1 \ {\rm kHz})\big] \ = \ $

3

Am Eingang des Systems mit gleichen Parametern wie in der Teilaufgabe (2) liegt nun der Diracpuls nbsp;$x_1(t)$nbsp; an.
Welche Aussagen treffen für das Ausgangssignal  $y_1(t)$  zu?

	$y_1(t)$  ist gegenüber  $x_1(t)$  um eine Konstante gedämpft/verstärkt.
	$y_1(t)$  ist gegenüber  $x_1(t)$  verschoben.
	$y_1(t)$   weist gegenüber  $x_1(t)$  Verzerrungen auf.

4

Berechnen Sie das Signal  $y_2(t)$  als Systemantwort auf das Cosinussignal  $x_2(t)$. Welcher Signalwert tritt zum Zeitpunkt  $t = 0$  auf?

$y_2(t = 0) \ = \ $

5

Welche Aussagen treffen bezüglich der Signale  $x_3(t)$  und  $y_3(t)$  zu?

	$y_3(t)$  weist gegenüber  $x_3(t)$  keine Verzerrungen auf.
	$y_3(t)$  weist gegenüber  $x_3(t)$  Dämpfungsverzerrungen auf.
	$y_3(t)$  weist gegenüber  $x_3(t)$  Phasenverzerrungen auf.

Musterlösung

Musterlösung

(1)  Richtig sind dieh Aussagen 1 und 2:

• Mit $z_1 = 1$, $T_1 = 0$, $z_2 =0$ ist $h(t) = \delta(t)$ und dementsprechend $H(f) = 1$, so dass stets $y(t) = x(t)$ gelten wird.
• Jede verzerrungsfreie Kanalimpulsantwort $h(t)$ besteht aus einer einzigen Diracfunktion, zum Beispiel bei $t = T_1$.
• Dieser Fall ist im Modell durch $z_2 =0$ berücksichtigt. Damit lautet der Frequenzgang:

$$H(f)= z_1\cdot {\rm e}^{-{\rm j}\cdot \hspace{0.05cm}2 \pi f T_1} \ \Rightarrow \ y(t) = z_1 \cdot x(t- T_1).$$

• Dagegen wird der Kanal immer dann zu linearen Verzerrungen führen, wenn gleichzeitig $z_1$ und $z_2$ von Null verschieden sind.

(2)  Die Fouriertransformation der Impulsantwort $h(t)$ führt auf die Gleichung:

$$H(f) = z_1\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}+ z_2\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2} .$$

Mit $z_1 = 1$, $T_1 = 0$, $z_2 =0.5$ und $T_2 = 1 \ \rm ms$ erhält man daraus:

$$H(f) =1 + 0.5 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2}.$$

Aufgeschlüsselt nach Real– und Imaginärteil liefert dies:

$${\rm Re}[H(f)] = 1 + 0.5 \cdot \cos(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Re}[H(f = f_1 =1 \ \rm kHz)] = 1.5}, $$

$${\rm Im}[H(f)] = -0.5 \cdot \sin(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Im}[H(f = f_1 =1 \ \rm kHz)] = 0}, $$

(3)  Richtig ist nur die erste Antwort:

• Aus dem Ergebnis zu (2) folgt für alle Vielfachen von $f_1 =1 \ \rm kHz$ die Betragsfunktion $|H(f)| = 1.5$ und die Phasenfunktion $b(f) = 0$.
• Damit ist für diese diskreten Frequenzwerte auch die Phasenlaufzeit jeweils $0$.
• Da aber das Spektrum $X_1(f)$ des Diracpulses genau bei diesen Frequenzen Spektrallinien aufweist, gilt $y_1(t) = 1.5 \cdot x_1(t)$.

(4)  Die Betragsfunktion lautet:

$$|H(f)| = \sqrt{{\rm Re}[H(f)]^2 + {\rm Im}[H(f)]^2} $$

$$\Rightarrow \; |H(f)| = \sqrt{1 + 0.25 \cdot \cos^2(2 \pi f \cdot T_2)+ \cos(2 \pi f \cdot T_2) + 0.25 \cdot \sin^2(2 \pi f \cdot T_2)} = \sqrt{1.25 + \cos(2 \pi f \cdot T_2) }.$$

Für die Frequenz $f_2 =0.25 \ \rm kHz$ erhält man somit:

$$|H(f)| = \sqrt{1.25 + \cos(\frac{\pi}{2} ) }= \sqrt{1.25} = 1.118.$$

Die Phasenfunktion lautet allgemein bzw. bei der Frequenz $f_2 =0.25 \ \rm kHz$:

$$b(f) = - {\rm arctan}\hspace{0.1cm}\frac{{\rm Im}[H(f)]}{{\rm Re}[H(f)]} = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin(2 \pi f T_2)}{1+0.5 \cdot \cos(2 \pi f T_2)},$$

$$b(f = f_2) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( \pi/2)}{1+0.5 \cdot \cos(\pi/2)}={\rm arctan}\hspace{0.1cm}\frac{0.5}{1} = 0.464.$$

Damit beträgt die Phasenlaufzeit für diese Frequenz:

$$\tau_2 = \frac {b(f_2)}{2 \pi f_2} = \frac {0.464}{2 \pi \cdot 0.25\,{\rm kHz}} \approx 0.3\,{\rm ms},$$

und es gilt für das Ausgangssignal:

$$y_2(t) = 1.118 \cdot \cos(2 \pi \cdot 0.25\,{\rm kHz}\cdot (t - 0.3\,{\rm ms})).$$

Der Signalwert zum Nullzeitpunkt ist somit:

$$y_2(t=0) = 1.118 \cdot \cos(-2 \pi \cdot 0.25\,{\rm kHz} \cdot 0.3\,{\rm ms}) \approx 1.118 \cdot 0.891 \hspace{0.15cm}\underline{= 0.996}.$$

(5)  Beide Frequenzen werden mit dem gleichen Dämpfungsfaktor $\alpha = 1.118$ beaufschlagt; daher sind keine Dämpfungsverzerrungen festzustellen.

Mit $f_3 = 1.25 \ \rm kHz$ und $T_2 = 1 \ \rm ms$ ergibt sich für die Phasenfunktion:

$$b(f = f_3) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( 2.5 \pi)}{1+0.5 \cdot \cos(2.5 \pi)}= 0.464 = b(f = f_2),$$

also genau der gleiche Wert wie bei der Frequenz $f_2 = 0.25 \ \rm kHz$. Trotzdem kommt es aber nun zu Phasenverzerrungen, da für $f_3$ die Phasenlaufzeit nur mehr $\tau = 60 \ μ \rm s$ beträgt.

Für das Ausgangssignal kann also geschrieben werden:

$$y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot (t - 0.3\,{\rm ms}) + 1.118 \cdot \cos(2 \pi f_3 \cdot (t - 0.06\,{\rm ms})$$

$$\Rightarrow \; \; y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot t - 27^\circ) + 1.118 \cdot \cos(2 \pi f_3 \cdot t - 27^\circ).$$

Richtig ist also die Antwort 3:

• Es gibt also Phasenverzerrungen, obwohl für beide Schwingungen $\varphi_2 = \varphi_3= 27^\circ$ gilt.
• Damit keine Phasenverzerrungen auftreten, müssten
  • die Phasenlaufzeiten $\tau_2$ und $\tau_3$ gleich sein, und
  • die Phasenwerte $\varphi_2$ und $\varphi_3$ linear mit den zugehörigen Frequenzen ansteigen.