Aufgaben:Aufgabe 1.4: Zeigerdiagramm und Ortskurve

• Zurück zum Buch

Vorgegebenes nalytisches Signal in der komplexen Ebene

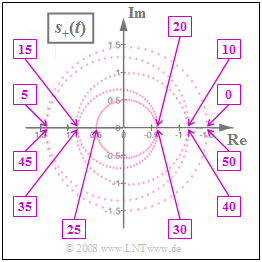
Die beiliegende Grafik zeigt das analytische Signal  $s_+(t)$  in der komplexen Ebene.

• Die in den Rechtecken angegebenen Zahlen geben die Zeitpunkte in Mikrosekunden an.
• Bei allen Vielfachen von  $5 \ \rm µ s$  ist  $s_+(t)$  stets reell und hat dabei folgende Werte:

$$s_+(t = 0) =s_+(t = 50\;{\rm µ s})= 1.500\hspace{0.05cm},$$

$$s_+(t = 5\;{\rm µ s}) = s_+(t = 45\;{\rm µ s})= -1.405\hspace{0.05cm},$$

$$s_+(t = 10\;{\rm µ s}) = s_+(t = 40\;{\rm µ s})= 1.155\hspace{0.05cm},$$

$$\text{.....................................} $$

$$s_+(t = 25\;{\rm µ s}) = -0.500\hspace{0.05cm}.$$

Als bekannt vorausgesetzt wird, dass das dazugehörige physikalische Signal folgende Form hat:

$$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T}\cdot t\right) + {A_0}/{2}\cdot \cos\left(\left(\omega_{\rm T} + \omega_{\rm 0}\right)\cdot t \right) + {A_0}/{2}\cdot \cos\left(\left(\omega_{\rm T} - \omega_{\rm 0}\right)\cdot t \right)\hspace{0.05cm}.$$

Gegeben ist die Frequenz des Trägersignals zu  $f_{\rm T} = 100\text{ kHz}$. Ermittelt werden sollen die drei weiteren Parameter  $f_0$,  $A_{\rm T}$  und  $A_0$.

Bezug genommen wird auch auf das  äquivalente TP–Signal  $s_{\rm TP}(t)$, wobei folgender Zusammenhang mit dem analytischen Signal besteht:

$$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{-{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Allgemeines Modell der Modulation.
• Bezug genommen wird insbesondere auf die Seite  Beschreibung von s(t) mit Hilfe des äquivalenten Tiefpass-Signals.
• Weitere Informationen zu dieser Thematik finden Sie in den Kapiteln des Buches „Signaldarstellung”:

(1)   Harmonische Schwingung,

(2)  Analytisches Signal und zugehörige Spektralfunktion  und

(3)  Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion.

• In unserem Tutorial $\rm LNTwww$ wird die Darstellung des analytischen Signals  $s_+(t)$  in der komplexen Ebene teilweise auch als „Zeigerdiagramm” bezeichnet, während die „Ortskurve” den zeitlichen Verlauf des äquivalenten TP–Signals  $s_{\rm TP}(t)$  angibt. Wir verweisen auf die entsprechenden interaktiven Applets

(1)  Physikalisches Signal & analytisches Signal ,

(2)  Physikalisches Signal & äquivalentes TP-Signal.

Fragebogen

1

Geben Sie ausgehend von $s(t)$ die Gleichung für  $s_+(t)$  an und vereinfachen Sie diese.
Welche Gleichung gilt für das äquivalente Tiefpass–Signal?

	Es gilt   $s_{\rm TP}(t) = A_0 · {\rm e}^{–{\rm j}ω_0t}.$
	Es gilt   $s_{\rm TP}(t) = A_{\rm T} + A_0 · {\rm e}^{+{\rm j}ω_0t}.$
	Es gilt   $s_{\rm TP}(t) = A_{\rm T} + A_0 · \cos(ω_0t).$

2

Bestimmen Sie den Signalparameter  $f_0$.

$f_0 \ = \ $ $\ \text{kHz}$

3

Bestimmen Sie die weiteren Signalparameter  $A_{\rm T}$  und  $A_0$.

$A_{\rm T} \ = \ $

$A_0 \ = \ $

4

Berechnen Sie die Werte des analytischen Signals  $s_+(t)$  zu den Zeiten  $t = 15 \;{\rm µ s}$  und  $t = 20\;{\rm µ s}$.

$s_+(t = 15 \ \rm µ s) \ = \ $

$s_+(t = 20 \ \rm µ s) \ = \ $

Musterlösung

Musterlösung

(1)  Alle Cosinusfunktionen sind in entsprechende komplexe Exponentialfunktionen umzuwandeln:

$$s_+(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.03cm}t} + \frac{A_0}{2}\cdot {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}(\omega_{\rm T} + \omega_{\rm 0})\hspace{0.03cm}\cdot \hspace{0.05cm}t} + \frac{A_0}{2}\cdot {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}(\omega_{\rm T} - \omega_{\rm 0})\hspace{0.03cm}\cdot \hspace{0.03cm}t} = {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.03cm}t} \cdot \left[ A_{\rm T}+ \frac{A_0}{2} \cdot \left( {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 0}\cdot \hspace{0.05cm}t} + {\rm e}^{\hspace{0.03cm}-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 0}\cdot \hspace{0.05cm}t}\right)\right]\hspace{0.05cm}.$$

Mit der Gleichung ${\rm e}^{{\rm j} · α} + {\rm e}^{-{\rm j} · α} = 2 · \cos(α)$ folgt weiter:

$$s_+(t) = {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.03cm}t} \cdot \left[ A_{\rm T}+ {A_0} \cdot \cos (\omega_{\rm 0}\cdot t) \right] \hspace{0.05cm}.$$

Damit erhält man für das äquivalente Tiefpass–Signal:

$$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{-{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} = A_{\rm T}+ {A_0} \cdot \cos (\omega_{\rm 0}\cdot t) \hspace{0.05cm}.$$

Richtig ist also der letzte Lösungsvorschlag.

• Im Kapitel „Hüllkurvendemodulation” des vorliegenden Buches werden wir sehen, dass es sich dabei um die Zweiseitenband–Amplitudenmodulation eines Cosinussignals mit cosinusförmigem Träger handelt.

(2)  Die Periodendauer des analytischen Signals $s_+(t)$ beträgt $T_0 = 50$ μs.

• Das physikalische Signal $s(t)$ hat die gleiche Periodendauer.
• Unter der Voraussetzung, dass $f_{\rm T}$ ein ganzzahliges Vielfaches von $f_0$ ist (was stets zu überprüfen ist, aber für dieses Beispiel zutrifft), ergibt sich $f_0 = 1/T_0 \hspace{0.15cm}\underline{ = 20 \ \rm kHz}$.

(3)  Bei den gegebenen Zeitpunkten (Vielfache von $5$ μs) gilt für den komplexen Drehzeiger des Trägers:

$${\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \cdot \hspace{0.05cm} {100\,{\rm kHz}}\cdot \hspace{0.05cm}(k \hspace{0.05cm}\cdot \hspace{0.05cm} 5\,{\rm \mu s})} = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}k \hspace{0.03cm} \cdot \hspace{0.05cm} \pi } = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{falls}} \\ {\rm{falls}} \\ \end{array}\begin{array}{*{20}c} k \hspace{0.1cm}{\rm gerade} , \\ k \hspace{0.1cm}{\rm ungerade} . \\ \end{array}$$

Deshalb folgt aus der in der Teilaufgabe (1) berechneten Gleichung:

$$k = 0 \Rightarrow \hspace{0.2cm} s_{\rm +}(t = 0) = A_{\rm T}+ {A_0} \cdot \cos (\omega_{\rm 0}\cdot 0) = A_{\rm T}+ {A_0} \hspace{0.05cm},$$

$$k = 5 \Rightarrow \hspace{0.2cm} s_{\rm +}(t = 25\;{\rm µ s}) = - \left[ A_{\rm T}+ {A_0} \cdot \cos (\omega_{\rm 0}\cdot {T_0}/{2}) \right] = -A_{\rm T}+ {A_0} \hspace{0.05cm}.$$

Ein Vergleich mit der ersten und letzten Gleichung auf dem Angabenblatt zeigt:

$$ s_{\rm +}(t = 0) = A_{\rm T}+ {A_0}=1.5 \hspace{0.05cm}, $$

$$ s_{\rm +}(t = 25\;{\rm \mu s}) = -A_{\rm T}+ {A_0} = -0.5 \hspace{0.05cm}.$$

Daraus erhält man $A_{\rm T} \hspace{0.15cm}\underline{ = 1}$ und $A_0 \hspace{0.15cm}\underline{ = 0.5}$.

(4)  Zum Zeitpunkt $t = 15$ μs ($k = 3$, ungerade) gilt:

$$ s_{\rm +}(t = 15\;{\rm µ s}) = - \left[ 1+ 0.5 \cdot \cos (2 \pi \cdot 20\,{\rm kHz} \cdot 0.015\,{\rm ms}) \right] \hspace{0.05cm}, = -1- 0.5 \cdot \cos (108^{\circ})\hspace{0.15cm}\underline {= -0.845} \hspace{0.05cm}.$$

Dagegen ergibt sich für den Zeitpunkt $t = 20$ μs ($k = 4$, gerade):

$$ s_{\rm +}(t = 20\;{\rm µ s}) = 1 + 0.5 \cdot \cos (144^{\circ})\hspace{0.15cm}\underline {= 0.595} \hspace{0.05cm}.$$

Bei allen diesen betrachteten Zeitpunkten ist das physikalische Signal $s(t) = {\rm Re}[s_+(t)]$ genau so groß.