Mobile Kommunikation/Die Charakteristika von GSM: Unterschied zwischen den Versionen
| Zeile 80: | Zeile 80: | ||
== Modulationsverfahren bei GSM== | == Modulationsverfahren bei GSM== | ||
<br> | <br> | ||
| − | Bei GSM steht pro Frequenzkanal lediglich eine Bandbreite von $B = 200 \ \rm kHz$ zur Verfügung, in der eine Gesamtdatenrate (für acht Nutzer) von $R_{\rm ges} = 270.833 \ \rm kbit/s$ übertragen werden muss. Man benötigt deshalb ein Modulationsverfahren mit einer Bandbreiteneffizienz von | + | Bei GSM steht pro Frequenzkanal lediglich eine Bandbreite von $B = 200 \ \rm kHz$ zur Verfügung, in der eine Gesamtdatenrate (für acht Nutzer) von $R_{\rm ges} = 270.833 \ \rm kbit/s$ übertragen werden muss. Man benötigt deshalb ein Modulationsverfahren mit einer Bandbreiteneffizienz von mindestens |
::<math>\beta \ge {R_{\rm ges}}/{B} \approx 1.35 \,\,{\rm bit/s/Hz}.</math> | ::<math>\beta \ge {R_{\rm ges}}/{B} \approx 1.35 \,\,{\rm bit/s/Hz}.</math> | ||
| − | GSM verwendet das sehr bandbreiteneffiziente Modulationsverfahren [[Modulationsverfahren/Nichtlineare_Modulationsverfahren#GMSK_.E2.80.93_Gaussian_Minimum_Shift_Keying|Gaussian Minimum Shift Keying]] (GMSK). Es sei nochmals ausdrücklich erwähnt, dass sich dieses Modulationsverfahren ebenso wie der FDMA/TDMA–Vielfachzugriff ausschließlich auf die Funkschnittstelle zwischen der <i>Mobile Station</i> (MS) und der <i>Base Transceiver Station </i> (BTS) bezieht, die in der [[Mobile_Kommunikation/Die_Charakteristika_von_GSM#Systemarchitektur_und_Basiseinheiten_von_GSM|Systemarchitektur–Grafik]] zu Beginn des Kapitels durch gelbe Hinterlegung hervorgehoben ist.<br> | + | GSM verwendet das sehr bandbreiteneffiziente Modulationsverfahren [[Modulationsverfahren/Nichtlineare_Modulationsverfahren#GMSK_.E2.80.93_Gaussian_Minimum_Shift_Keying|Gaussian Minimum Shift Keying]] (GMSK). Es sei nochmals ausdrücklich erwähnt, dass sich dieses Modulationsverfahren ebenso wie der FDMA/TDMA–Vielfachzugriff ausschließlich auf die Funkschnittstelle zwischen der <i>Mobile Station</i> (MS) und der <i>Base Transceiver Station </i> (BTS) bezieht, die in der [[Mobile_Kommunikation/Die_Charakteristika_von_GSM#Systemarchitektur_und_Basiseinheiten_von_GSM|Systemarchitektur–Grafik]] zu Beginn des Kapitels durch gelbe Hinterlegung hervorgehoben ist.<br> |
| − | GMSK wurde bereits im Kapitel [[Modulationsverfahren/Nichtlineare_Modulationsverfahren#Eigenschaften_nichtlinearer_Verfahren| Eigenschaften nichtlinearer Verfahren]] des Buches „Modulationsverfahren” beschrieben. Hier werden | + | GMSK wurde bereits im Kapitel [[Modulationsverfahren/Nichtlineare_Modulationsverfahren#Eigenschaften_nichtlinearer_Verfahren| Eigenschaften nichtlinearer Verfahren]] des Buches „Modulationsverfahren” beschrieben. Hier werden die wesentlichen Eigenschaften kurz zusammengefasst. |
| − | *GMSK ist eine Sonderform von binärem [[Modulationsverfahren/Nichtlineare_digitale_Modulation#FSK_.E2.80.93_Frequency_Shift_Keying| Frequency Shift Keying]] (FSK). Voraussetzung für die Orthogonalität zwischen den beiden Signalformen ist, dass der Modulationsindex $h$ ein Vielfaches von $0.5$ ist. Für ganzzahlige Werte von $h$ kann die Demodulation auch nichtkohärent erfolgen.<br> | + | *GMSK ist eine Sonderform von binärem [[Modulationsverfahren/Nichtlineare_digitale_Modulation#FSK_.E2.80.93_Frequency_Shift_Keying| Frequency Shift Keying]] (FSK). Voraussetzung für die Orthogonalität zwischen den beiden Signalformen ist, dass der Modulationsindex $h$ ein Vielfaches von $0.5$ ist. Für ganzzahlige Werte von $h$ kann die Demodulation auch nichtkohärent erfolgen.<br> |
| − | *Bei GSM verwendet man den kleinstmöglichen Modulationsindex $h = 0.5$. Ein größerer Wert würde eine deutlich größere Bandbreite beanspruchen. Eine solche FSK mit $h = 0.5$ nennt man auch [[Modulationsverfahren/Nichtlineare_Modulationsverfahren#MSK_.E2.80.93_Minimum_Shift_Keying| Minimum Shift Keying]] (MSK). Allerdings ist dann eine kohärente Demodulation erforderlich.<br> | + | *Bei GSM verwendet man den kleinstmöglichen Modulationsindex $h = 0.5$. Ein größerer Wert würde eine deutlich größere Bandbreite beanspruchen. Eine solche FSK mit $h = 0.5$ nennt man auch [[Modulationsverfahren/Nichtlineare_Modulationsverfahren#MSK_.E2.80.93_Minimum_Shift_Keying| Minimum Shift Keying]] (MSK). Allerdings ist dann eine kohärente Demodulation erforderlich.<br> |
| − | *Ein sehr schmales Spektrum ergibt sich allerdings erst dann, wenn die Phasenwerte an den Symbolgrenzen aneinander angepasst und dadurch Phasensprünge vermieden werden, was bei MSK gegeben ist. Man bezeichnet solche Verfahren als [[Modulationsverfahren/Nichtlineare_digitale_Modulation#Bin.C3.A4re_FSK_mit_kontinuierlicher_Phasenanpassung| Continuous Phase Frequency Shift Keying]] (CP–FSK).<br> | + | *Ein sehr schmales Spektrum ergibt sich allerdings erst dann, wenn die Phasenwerte an den Symbolgrenzen aneinander angepasst und dadurch Phasensprünge vermieden werden, was bei MSK gegeben ist. Man bezeichnet solche Verfahren als [[Modulationsverfahren/Nichtlineare_digitale_Modulation#Bin.C3.A4re_FSK_mit_kontinuierlicher_Phasenanpassung| Continuous Phase Frequency Shift Keying]] (CP–FSK).<br> |
| − | *Bei GSM wird vor dem Frequenzmodulator noch ein Tiefpass mit Gauß–Charakteristik eingefügt ⇒ [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle#Modulation_bei_GSM.E2.80.93Systemen|Gaussian Minimum Shift Keying]] (GMSK), wodurch die Bandbreite weiter verringert und die Bandbreiteneffizienz verbessert wird.<br><br> | + | *Bei GSM wird vor dem Frequenzmodulator noch ein Tiefpass mit Gauß–Charakteristik eingefügt ⇒ [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle#Modulation_bei_GSM.E2.80.93Systemen|Gaussian Minimum Shift Keying]] (GMSK), wodurch die Bandbreite weiter verringert und die Bandbreiteneffizienz verbessert wird.<br><br> |
| − | Hinsichtlich der hier behandelten Thematik (kohärente bzw. nichtkohärente Demodulation von FSK) verweisen wir auf | + | Hinsichtlich der hier behandelten Thematik (kohärente bzw. nichtkohärente Demodulation von FSK) verweisen wir auf zwei Aufgaben im Buch „Digitalsignalübertragung”: |
| − | *[[Aufgaben:Aufgabe_4.16:_Binary_Frequency_Shift_Keying|Aufgabe 4.16: Binary Frequency Shift Keying]],<br> | + | *[[Aufgaben:Aufgabe_4.16:_Binary_Frequency_Shift_Keying|Aufgabe 4.16: Binary Frequency Shift Keying]],<br> |
| − | *[[Aufgaben:Aufgabe_4.18Z:_BER_von_kohärenter_und_nichtkohärenter_FSK|Aufgabe 4.18Z: BER von kohärenter und nichtkohärenter FSK]].<br><br> | + | *[[Aufgaben:Aufgabe_4.18Z:_BER_von_kohärenter_und_nichtkohärenter_FSK|Aufgabe 4.18Z: BER von kohärenter und nichtkohärenter FSK]].<br><br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ Die folgende Grafik soll die bisherigen Aussagen verdeutlichen: | $\text{Beispiel 1:}$ Die folgende Grafik soll die bisherigen Aussagen verdeutlichen: | ||
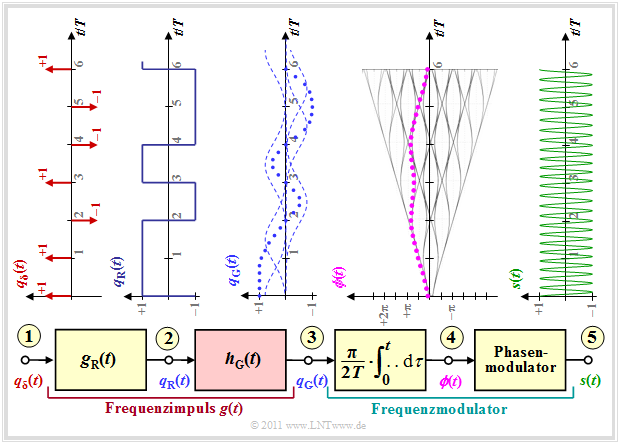
| − | [[Datei:P ID2206 Mob T 3 3 S4 v1.png| | + | [[Datei:P ID2206 Mob T 3 3 S4 v1.png|right|frame|Blockschaltbild und Signale bei GMSK|class=fit]] |
| − | *Ausgehend von einem diracförmigen Quellensignal $q_\delta(t)$ am Punkt $(1)$ kommt man durch ein Filter mit der rechteckförmigen Impulsantwort $g_{\rm R}(t)$ zum Rechtecksignal $q_{\rm R}(t)$ am Punkt $(2)$. | + | *Ausgehend von einem diracförmigen Quellensignal $q_\delta(t)$ am Punkt $(1)$ kommt man durch ein Filter mit der rechteckförmigen Impulsantwort $g_{\rm R}(t)$ zum Rechtecksignal $q_{\rm R}(t)$ am Punkt $(2)$. |
| − | *Würde man auf den Gaußtiefpass mit der Impulsantwort $h_{\rm G}(t)$ verzichten ⇒ $q_{\rm G}(t) = q_{\rm R}(t)$, so ergäbe sich am Punkt $(4)$ eine abschnittsweise lineare Phasenfunktion $\phi(t)$. Bei Vielfachen der Symboldauer $T$ wären damit alle Phasenwerte Vielfache von $π/2$. | + | *Würde man auf den Gaußtiefpass mit der Impulsantwort $h_{\rm G}(t)$ verzichten ⇒ $q_{\rm G}(t) = q_{\rm R}(t)$, so ergäbe sich am Punkt $(4)$ eine abschnittsweise lineare Phasenfunktion $\phi(t)$. Bei Vielfachen der Symboldauer $T$ wären damit alle Phasenwerte Vielfache von $π/2$. |
| − | *Nach dem Phasenmodulator würde dann am Punkt $(5)$ ein binäres FSK–Signal $s(t)$ mit nur zwei Frequenzen auftreten. | + | *Nach dem Phasenmodulator würde dann am Punkt $(5)$ ein binäres FSK–Signal $s(t)$ mit nur zwei Frequenzen auftreten. Dieses Signal ist aufgrund des bei Orthogonalität minimalen Modulationsindex $h = 0.5$ gleichzeitig ein MSK–Signal. |
| − | *Durch den Gaußtiefpass $H_{\rm G}(f)$ mit der Grenzfrequenz $f_{\rm G}= 0.45/T$ (gültig für GSM) ist der Frequenzimpuls $g(t)$ nicht mehr rechteckförmig, sondern entspricht der Rechteckantwort von $H_{\rm G}(f)$. Gemäß Fouriertransformation gilt $g(t) = g_{\rm R}(t) \star h_{\rm G}(t)$. | + | *Durch den Gaußtiefpass $H_{\rm G}(f)$ mit der Grenzfrequenz $f_{\rm G}= 0.45/T$ (gültig für GSM) ist der Frequenzimpuls $g(t)$ nicht mehr rechteckförmig, sondern entspricht der Rechteckantwort von $H_{\rm G}(f)$. Gemäß Fouriertransformation gilt $g(t) = g_{\rm R}(t) \star h_{\rm G}(t)$. |
| − | *Somit | + | *Somit verläuft die Phasenfunktion $\phi(t)$ nicht mehr abschnittsweise linear, sondern die Ecken sind abgerundet, wie aus dem Signalverlauf am Punkt $(4)$ zu ersehen ist. Die violett–gepunktete Kurve gilt für die am Punkt $(1)$ angenommene Datenfolge. |
| − | + | <br clear=all> | |
| − | + | Das GMSK–Signal $s(t)$ beinhaltet nun deutlich mehr als nur zwei diskrete Frequenzen und das Leistungsdichtespektrum fällt schneller ab, wie das [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle#Vor.E2.80.93_und_Nachteile_von_GMSK| Diagramm]] im Buch „Beispiele von Nachrichtensystemen” zeigt. Aus der obigen Zeitdarstellung des Sendesignals $s(t)$ am Punkt $(5)$ des Blockschaltbildes ist dieser Sachverhalt allerdings nur schwer zu erkennen.}} | |
| − | |||
== GSM–Erweiterungen == | == GSM–Erweiterungen == | ||
Version vom 17. April 2019, 14:21 Uhr
Inhaltsverzeichnis
Systemarchitektur und Basiseinheiten von GSM
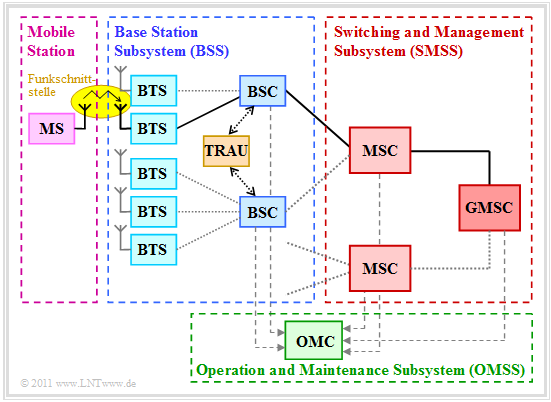
GSM (Global System for Mobile Communication) ist ein stark hierarchisch gegliedertes System verschiedener Netzkomponenten. Aus der Grafik erkennt man:
- Die Mobilstation (MS) kommuniziert über die Funkschnittstelle mit der nächstgelegenen Base Transceiver Station (BTS, Sende– und Empfangsbasisstation).
- Mehrere solcher BTS werden gebietsweise zusammengefasst und sind gemeinsam einem Base Station Controller (BSC, Kontrollstation) unterstellt.
- Das Base Station Subsystem (BSS) besteht aus einer Vielzahl von BTS und mehreren BSC. In der Grafik ist ein solches BSS blau umrandet.
- Jeder BSC ist mit einem Mobile Switching Center (MSC, Vermittlungsrechner) verbunden, dessen Funktion mit einem Vermittlungsknoten im Festnetz vergleichbar ist.
- Das Gateway Mobile Switching Center (GMSC) ist für die Verbindung zwischen Fest– und Mobilfunknetz zuständig. Wird zum Beispiel ein Mobilfunkteilnehmer aus dem Festnetz angerufen, so ermittelt das GMSC das zuständige MSC und vermittelt den Ruf weiter.
- Das Operation and Maintenance Center (OMC) überwacht einen Teil des Mobilfunknetzes. Daneben übernimmt es auch organisatorische Aufgaben wie Steuerung des Verkehrsflusses, Gebührenerfassung, Sicherheitsmanagement, usw.
Genauere Informationen zur GSM–Systemarchitektur und zu den einzelnen Netzkomponenten finden Sie im Kapitel Allgemeine Beschreibung von GSM des Buches „Beispiele von Nachrichtensystemen”.
Vielfachzugriff bei GSM
Bei GSM werden zwei Vielfachzugriffsverfahren parallel verwendet:
- Frequenzmultiplex (Frequency Division Multiple Access, FDMA),
- Zeitmultiplex (Time Division Multiple Access, TDMA).
Die Grafik und die folgende Beschreibung gilt für das ursprüngliche System „GSM 900” (D–Netz). Für „GSM/DCS 1800” (E–Netz) gelten vergleichbare Aussagen.
- Im D–Netz werden für Uplink und Downlink jeweils eine Bandbreite von $25\ \rm MHz$ bereit gestellt $($Duplexabstand: $45\ \rm MHz)$. Man spricht von Frequency Division Duplex (FDD). Beim E–Netz beträgt die Bandbreite jeweils $75\ \rm MHz$ und der Duplexabstand ist $95\ \rm MHz$.
- Uplink– und Downlinkband werden in Frequenzbänder der Breite $200\ \rm kHz$ unterteilt. Unter Berücksichtigung von Schutzbereichen an den jeweiligen Rändern stehen somit $N_{\rm F} = 124$ (im D–Netz) bzw. $N_{\rm F} = 374$ (im E–Netz) Frequenzkanäle zur Verfügung.
- Jeder Zelle wird eine Teilmenge der Frequenzen zugewiesen ⇒ Cell Allocation. Benachbarte Zellen arbeiten meist bei unterschiedlichen Frequenzen, zum Beispiel mit dem Reuse–Faktor $3$, wie im Abschnitt Zellulare Architektur durch die Farben Weiß, Gelb, Blau angedeutet.
- Die $124$ GSM–Frequenzkanäle werden durch Zeitmultiplex (TDMA) weiter unterteilt. Jeder FDMA–Kanal wird in so genannte TDMA–Rahmen aufgeteilt, die ihrerseits jeweils $N_{\rm T} = 8$ Zeitschlitze (Time–Slots) umfassen.
- Die Slots werden periodisch den einzelnen GSM–Nutzern zugeordnet und beinhalten jeweils einen so genannten Burst. Jedem Nutzer steht in jedem TDMA–Rahmen ein Zeitschlitz zur Verfügung. Eine Bündelung (maximal sechs pro User) ist nur bei GPRS/EDGE möglich.
- Die TDMA–Rahmen des Uplinks werden gegenüber denen des Downlinks um drei Slots verzögert gesendet: Time Division Duplex (TDD). Die Hardware der Mobilstation kann somit gleichermaßen zum Senden und Empfangen einer Nachricht verwendet werden.
Daten– und Rahmenstruktur bei GSM
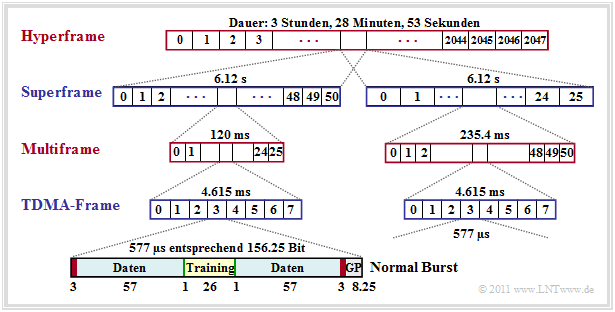
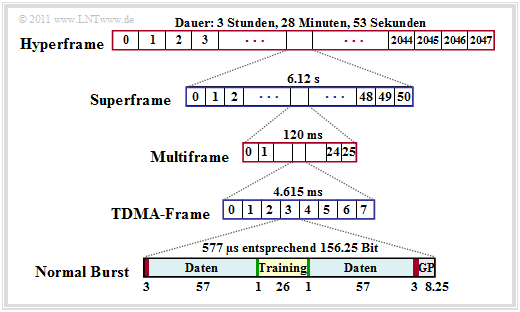
Durch die GSM–Rahmenstruktur erfolgt die Abbildung der logischen Kanäle auf physikalische Kanäle. Hier beschränken wir uns auf Verkehrskanäle und auf die Abbildung in der Zeit. In diesem Fall wird jeder Multiframe von $120 \ \rm ms$ Dauer in $26$ TDMA–Rahmen (davon zwei für Kontrollkanäle) der Dauer $4.615\ \rm ms$ unterteilt. Damit ergibt sich für die Dauer eines Zeitschlitzes näherungsweise $T_{\rm Z} = 576.9\ \rm µ s$.
Man erkennt aus dieser Grafik:
- In jedem Zeitschlitz wird ein so genannter Burst übertragen, dessen Zeitdauer einheitlich $156.25$ Bitdauern entspricht. Daraus folgt für die Bitdauer $T_{\rm B} = 576.9\ \rm µ s/156.25 ≈ 3.692 \ \rm µs$ und für die Gesamt–Bruttodatenrate:
- \[R_{\rm ges} = {1}/{T_{\rm B}}= 270.833\,{\rm kbit/s}\hspace{0.05cm}.\]
- Die Bruttodatenrate eines jeden Nutzers ist somit $R_{\rm Brutto} = 33.854 \ \rm kbit/s$. Da in jedem Normal Burst aber nur $2 · 57 = 114$ Datenbit (in der Grafik blau hinterlegt) übertragen werden, ergibt sich die klerinere Nettodatenrate mit $R_{\rm Netto} = 22.8 \ \rm kbit/s$.
- Diese Nettodatenrate berücksichtigt auch die Kanalcodierung. Bei einem Sprachsignal werden pro $20\ \rm kbit/s$–Sprachrahmen $456$ Bit übertragen, woraus sich genau die Rate $22.8 \ \rm kbit/s$ ergibt. Ohne Kanalcodierung wäre die Datenrate nur $13 \ \rm kbit/s$.
- Neben den Verkehrsdaten enthält ein Normal Burst noch
- – zweimal drei Tailbits (rot, in dieser Zeit wird der Kanal neu vermessen),
- – zwei Signalisierungsbits (grün),
- – die Guard Period (GP) mit $8.25$ Bitdauern $($grau, ca. $30.5 \ \rm µ s)$, sowie
- – $26$ Bit für die Trainingssequenz (zur Kanalschätzung und Synchronisation),
wodurch sich die Datenrate von $22.8$ auf $33.854 \ \rm kbit/s$ erhöht.
Anmerkung:
- Bei GSM spielen neben dem Normal Burst noch andere Arten von Bursts (Frequency Correction Burst, Synchronization Burst, Dummy Burst, Access Burst ) eine Rolle.
- Alle diese Bursts haben eine einheitliche Länge von $156.25$ Bitdauern. Hierauf wird in der Aufgabe 3.2 genauer eingegangen.
Modulationsverfahren bei GSM
Bei GSM steht pro Frequenzkanal lediglich eine Bandbreite von $B = 200 \ \rm kHz$ zur Verfügung, in der eine Gesamtdatenrate (für acht Nutzer) von $R_{\rm ges} = 270.833 \ \rm kbit/s$ übertragen werden muss. Man benötigt deshalb ein Modulationsverfahren mit einer Bandbreiteneffizienz von mindestens
- \[\beta \ge {R_{\rm ges}}/{B} \approx 1.35 \,\,{\rm bit/s/Hz}.\]
GSM verwendet das sehr bandbreiteneffiziente Modulationsverfahren Gaussian Minimum Shift Keying (GMSK). Es sei nochmals ausdrücklich erwähnt, dass sich dieses Modulationsverfahren ebenso wie der FDMA/TDMA–Vielfachzugriff ausschließlich auf die Funkschnittstelle zwischen der Mobile Station (MS) und der Base Transceiver Station (BTS) bezieht, die in der Systemarchitektur–Grafik zu Beginn des Kapitels durch gelbe Hinterlegung hervorgehoben ist.
GMSK wurde bereits im Kapitel Eigenschaften nichtlinearer Verfahren des Buches „Modulationsverfahren” beschrieben. Hier werden die wesentlichen Eigenschaften kurz zusammengefasst.
- GMSK ist eine Sonderform von binärem Frequency Shift Keying (FSK). Voraussetzung für die Orthogonalität zwischen den beiden Signalformen ist, dass der Modulationsindex $h$ ein Vielfaches von $0.5$ ist. Für ganzzahlige Werte von $h$ kann die Demodulation auch nichtkohärent erfolgen.
- Bei GSM verwendet man den kleinstmöglichen Modulationsindex $h = 0.5$. Ein größerer Wert würde eine deutlich größere Bandbreite beanspruchen. Eine solche FSK mit $h = 0.5$ nennt man auch Minimum Shift Keying (MSK). Allerdings ist dann eine kohärente Demodulation erforderlich.
- Ein sehr schmales Spektrum ergibt sich allerdings erst dann, wenn die Phasenwerte an den Symbolgrenzen aneinander angepasst und dadurch Phasensprünge vermieden werden, was bei MSK gegeben ist. Man bezeichnet solche Verfahren als Continuous Phase Frequency Shift Keying (CP–FSK).
- Bei GSM wird vor dem Frequenzmodulator noch ein Tiefpass mit Gauß–Charakteristik eingefügt ⇒ Gaussian Minimum Shift Keying (GMSK), wodurch die Bandbreite weiter verringert und die Bandbreiteneffizienz verbessert wird.
Hinsichtlich der hier behandelten Thematik (kohärente bzw. nichtkohärente Demodulation von FSK) verweisen wir auf zwei Aufgaben im Buch „Digitalsignalübertragung”:
- Aufgabe 4.16: Binary Frequency Shift Keying,
- Aufgabe 4.18Z: BER von kohärenter und nichtkohärenter FSK.
$\text{Beispiel 1:}$ Die folgende Grafik soll die bisherigen Aussagen verdeutlichen:
- Ausgehend von einem diracförmigen Quellensignal $q_\delta(t)$ am Punkt $(1)$ kommt man durch ein Filter mit der rechteckförmigen Impulsantwort $g_{\rm R}(t)$ zum Rechtecksignal $q_{\rm R}(t)$ am Punkt $(2)$.
- Würde man auf den Gaußtiefpass mit der Impulsantwort $h_{\rm G}(t)$ verzichten ⇒ $q_{\rm G}(t) = q_{\rm R}(t)$, so ergäbe sich am Punkt $(4)$ eine abschnittsweise lineare Phasenfunktion $\phi(t)$. Bei Vielfachen der Symboldauer $T$ wären damit alle Phasenwerte Vielfache von $π/2$.
- Nach dem Phasenmodulator würde dann am Punkt $(5)$ ein binäres FSK–Signal $s(t)$ mit nur zwei Frequenzen auftreten. Dieses Signal ist aufgrund des bei Orthogonalität minimalen Modulationsindex $h = 0.5$ gleichzeitig ein MSK–Signal.
- Durch den Gaußtiefpass $H_{\rm G}(f)$ mit der Grenzfrequenz $f_{\rm G}= 0.45/T$ (gültig für GSM) ist der Frequenzimpuls $g(t)$ nicht mehr rechteckförmig, sondern entspricht der Rechteckantwort von $H_{\rm G}(f)$. Gemäß Fouriertransformation gilt $g(t) = g_{\rm R}(t) \star h_{\rm G}(t)$.
- Somit verläuft die Phasenfunktion $\phi(t)$ nicht mehr abschnittsweise linear, sondern die Ecken sind abgerundet, wie aus dem Signalverlauf am Punkt $(4)$ zu ersehen ist. Die violett–gepunktete Kurve gilt für die am Punkt $(1)$ angenommene Datenfolge.
Das GMSK–Signal $s(t)$ beinhaltet nun deutlich mehr als nur zwei diskrete Frequenzen und das Leistungsdichtespektrum fällt schneller ab, wie das Diagramm im Buch „Beispiele von Nachrichtensystemen” zeigt. Aus der obigen Zeitdarstellung des Sendesignals $s(t)$ am Punkt $(5)$ des Blockschaltbildes ist dieser Sachverhalt allerdings nur schwer zu erkennen.
GSM–Erweiterungen
GSM wurde als europäisches Mobilfunksystem für Telefongespräche konzipiert und entwickelt mit der Zusatzoption der Datenübertragung, aber nur mit geringer Datenrate $(9.6 \ \rm kbit/s)$. Die Standardisierung der GSM–Phase 2 ab 1995 beinhaltete aber bereits erste Weiterentwicklungen und einige neue, bereits von ISDN bekannte und von den Nutzern geschätzte Zusatzdienste.
In den Jahren von 1997 bis 2000 wurden neue Datendienste mit höheren Bitraten entwickelt, die man der GSM–Phase 2+ (bzw. 2.5) zurechnet:
- High–Speed Circuit–Switched Data (HSCSD) bietet bei ausreichend gutem Kanal durch eine höhere Coderate (Punktierung des Faltungscodes) eine leitungsorientierte Übertragung mit $14.4 \ \rm kbit/s$ (gegenüber $9.6 \ \rm kbit/s$). Es ermöglicht zudem eine Kanalbündelung durch die Kombination mehrerer Zeitschlitze ⇒ „Multislot Capability”. Bei einer Bündelung von vier Zeitschlitzen kommt man so auf eine maximale Übertragungsrate von $57.6 \ \rm kbit/s$.
- General Packet Radio Service (GPRS) ermöglicht die Kommunikation mit anderen Netzen wie etwa dem Internet oder firmeninternen Intranets. Es ist paketorientiert (statt leitungsorientiert) und unterstützt viele Datenübertragungsprotokolle, zum Beispiel das Internet Protocol (IP), X.25 und Datex–P. Die Gebühren ergeben sich bei GPRS nicht aus der Verbindungsdauer, sondern aus der übertragenen Datenmenge. Ein GPRS–Nutzer profitiert von den kürzeren Zugriffszeiten und der höheren Datenrate bis $21.4 \ \rm kbit/s$. Durch die Bündelung von sechs Zeitschlitzen erreicht man so maximal $128.4 \ \rm kbit/s$.
- Enhanced Data Rates for GSM Evolution (EDGE) benutzt neben dem GSM–Standard GMSK als weiteres Modulationsverfahren 8–PSK, so dass mit jedem Symbol drei Datenbits übertragen werden und auf diese Weise die Datenrate (theoretisch) verdreifacht werden kann.
Bei der Kombination aus GPRS und EDGE – man spricht dann von E–GPRS – gibt es neun verschiedene Modulation and Coding Schemes (MCS), zwischen denen der Betreiber wählen kann:
- mit GMSK– oder mit 8–PSK–Modulation,
- resultierende Coderaten zwischen $0.37$ und $1$, sowie
- Datenraten zwischen $8.8 \ \rm kbit/s$ (für MCS–1) und $59.2 \ \rm kbit/s$ (für MCS–9).
In der Praxis maximal anwendbar sind allerdings MCS–8 $(54.4 \ \rm kbit/s)$ und sieben Zeitschlitze. Damit erreicht man immerhin $380.8 \ \rm kbit/s$ und damit die Größenordnung von UMTS $(384 \ \rm kbit/s)$.
Erwähnt werden soll noch EDGE Evolution oder „Evolved EDGE”, also die Weiterentwicklung der Weiterentwicklung von GSM in Release 7 (Dezember 2007). Hierfür werden von den Entwicklern Datenraten bis zu $1 \ \rm Mbit/s$ und halbierte Latenzzeiten ($10 \ \rm ms$ statt $20 \ \rm ms$) angegeben.
- Man erreicht diese Werte unter Anderem durch 32–QAM– oder 16–QAM–Modulation anstelle von 8–PSK und eine verbesserte Fehlerkorrektur durch den Einsatz von Turbo–Codes.
- Außerdem wurde die Symbolrate von $270.833 \ \rm ksymbol/s$ um $20\%$ auf $325\ \rm ksymbol/s$ erhöht.
Aufgaben zum Kapitel
Zusatzaufgabe 3.5Z: GSM–Netzkomponenten