Signaldarstellung/Klassifizierung von Signalen: Unterschied zwischen den Versionen
| Zeile 68: | Zeile 68: | ||
| − | Im unteren Bild ist diese Kausalität nicht mehr gegeben. Wie leicht zu ersehen ist, kommt man | + | Im unteren Bild ist diese Kausalität nicht mehr gegeben. Wie leicht zu ersehen ist, kommt man bei diesem Beispiel schon durch eine zusätzliche Laufzeit von einer Millisekunde von der akausalen zur kausalen Darstellung.}} |
==Energiebegrenzte und leistungsbegrenzte Signale== | ==Energiebegrenzte und leistungsbegrenzte Signale== | ||
<br> | <br> | ||
| − | An dieser Stelle müssen zunächst zwei wichtige Signalbeschreibungsgrößen eingeführt werden, nämlich die '''Energie''' und die '''Leistung'''. | + | An dieser Stelle müssen zunächst zwei wichtige Signalbeschreibungsgrößen eingeführt werden, nämlich die '''Energie''' und die '''Leistung'''. |
*Im Sinne der Physik entspricht die Energie der Arbeit und hat zum Beispiel die Einheit „Ws“. | *Im Sinne der Physik entspricht die Energie der Arbeit und hat zum Beispiel die Einheit „Ws“. | ||
*Die Leistung ist als „Arbeit pro Zeit” definiert und besitzt somit die Einheit „W“. | *Die Leistung ist als „Arbeit pro Zeit” definiert und besitzt somit die Einheit „W“. | ||
| − | Beide Größen sind nach den elementaren Gesetzen der Elektrotechnik vom Widerstand $R$ abhängig. Um diese Abhängigkeit zu eliminieren, wird in der Nachrichtentechnik oftmals der Widerstand $R=1 \,\Omega$ zugrunde gelegt. Dann gelten folgende Definitionen: | + | Beide Größen sind nach den elementaren Gesetzen der Elektrotechnik vom Widerstand $R$ abhängig. Um diese Abhängigkeit zu eliminieren, wird in der Nachrichtentechnik oftmals der Widerstand $R=1 \,\Omega$ zugrunde gelegt. Dann gelten folgende Definitionen: |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Die '''Energie''' des Signals $x(t)$ ist wie folgt zu berechnen: | + | Die '''Energie''' des Signals $x(t)$ ist wie folgt zu berechnen: |
:$$E_x=\lim_{T_{\rm M}\to\infty} \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$}} | :$$E_x=\lim_{T_{\rm M}\to\infty} \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$}} | ||
| Zeile 88: | Zeile 88: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Zur Berechnung der (mittleren) '''Leistung''' muss vor dem Grenzübergang noch durch die Zeit $T_{\rm M}$ dividiert werden: | + | $\text{Definition:}$ Zur Berechnung der (mittleren) '''Leistung''' muss vor dem Grenzübergang noch durch die Zeit $T_{\rm M}$ dividiert werden: |
:$$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M} } \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$ | :$$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M} } \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$ | ||
| − | Hierbei bezeichnet $T_{\rm M}$ die symmetrisch bezüglich des Zeitursprungs $(t = 0)$ angenommene Messdauer, während der das Signal beobachtet wird. Dieses Zeitintervall muss im Allgemeinen sehr groß gewählt werden; im Idealfall sollte $T_{\rm M}$ gegen unendlich gehen.}} | + | Hierbei bezeichnet $T_{\rm M}$ die symmetrisch bezüglich des Zeitursprungs $(t = 0)$ angenommene Messdauer, während der das Signal beobachtet wird. Dieses Zeitintervall muss im Allgemeinen sehr groß gewählt werden; im Idealfall sollte $T_{\rm M}$ gegen unendlich gehen.}} |
| − | Bezeichnet $x(t)$ einen Spannungsverlauf mit der Einheit $\text{V}$, so hat nach obigen Gleichungen | + | Bezeichnet $x(t)$ einen Spannungsverlauf mit der Einheit $\text{V}$, so hat nach obigen Gleichungen |
| − | *die Signalenergie die Einheit $\text{V}^2\text{s}$, | + | *die Signalenergie die Einheit $\text{V}^2\text{s}$, |
| − | *die Signalleistung die Einheit $\text{V}^2$. | + | *die Signalleistung die Einheit $\text{V}^2$. |
| − | Diese Aussage bedeutet auch: Bei den obigen Definitionen liegt der Bezugswiderstand $R=1\,\Omega$ | + | Diese Aussage bedeutet auch: Bei den obigen Definitionen liegt bereits der Bezugswiderstand $R=1\,\Omega$ implizit zugrunde. |
| Zeile 106: | Zeile 106: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 3:}$ | $\text{Beispiel 3:}$ | ||
| − | Nun werden Energie und Leistung zweier beispielhafter Signale berechnet | + | Nun werden Energie und Leistung zweier beispielhafter Signale berechnet. |
| − | + | Die obere Grafik zeigt einen Rechteckimpuls $x_1(t)$ mit Amplitude $A$ und Dauer $T$. | |
| − | |||
| + | *Die Signalenergie dieses Impulses ist $E_1 = A^2 \cdot T$. | ||
| + | *Für die Signalleistung ergibt sich aufgrund der Division durch $T_{\rm M}$ und Grenzwertbildung $(T_{\rm M} \to \infty)$ der Wert $P_1 = 0$. | ||
| − | |||
| − | + | Beim Cosinussignal $x_2(t)$ mit der Amplitude $A$ entsprechend der unteren Skizze gilt: | |
| − | |||
| + | *Die Signalleistung ist unabhängig von der Frequenz gleich $P_2 = A^2/2$. | ||
| + | *Die Signalenergie $E_2$ (Integral über die Leistung für alle Zeiten) ist unendlich. | ||
| − | Mit $A = 4 {\rm V}$ ergibt sich für die Leistung $P_2 = 8 {\rm V}^2$. Mit dem Widerstand von $R = 50 \,\,\Omega$ entspricht dies der physikalischen Leistung ${8}/{50} \,\,{\rm V}\hspace{-0.1cm}/{\Omega}= 160\,\, {\rm mW}$.}} | + | |
| + | Mit $A = 4 \ {\rm V}$ ergibt sich für die Leistung $P_2 = 8 \ {\rm V}^2$. Mit dem Widerstand von $R = 50 \,\,\Omega$ entspricht dies der physikalischen Leistung ${8}/{50} \,\,{\rm V}\hspace{-0.1cm}/{\Omega}= 160\,\, {\rm mW}$.}} | ||
| Zeile 125: | Zeile 127: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Ein Signal $x(t)$ mit endlicher Energie $E_x$ und unendlich kleiner Leistung $(P_x = 0)$ bezeichnet man als '''energiebegrenzt'''.}} | + | Ein Signal $x(t)$ mit endlicher Energie $E_x$ und unendlich kleiner Leistung $(P_x = 0)$ bezeichnet man als '''energiebegrenzt'''.}} |
| − | *Impulsförmige Signale wie das Signal $x_1(t)$ im obigen Beispiel sind stets energiebegrenzt. Meist sind hier die Signalwerte nur für eine endliche Zeitdauer von Null verschieden. In anderen Worten: Solche Signale sind oft auch zeitbegrenzt. | + | *Impulsförmige Signale wie das Signal $x_1(t)$ im obigen Beispiel sind stets energiebegrenzt. Meist sind hier die Signalwerte nur für eine endliche Zeitdauer von Null verschieden. In anderen Worten: Solche Signale sind oft auch zeitbegrenzt. |
| − | *Aber auch zeitlich unbegrenzte Signale können durchaus eine endliche Energie besitzen. In späteren [[Signaldarstellung/Fouriertransformation_und_-rücktransformation|Kapiteln]] finden Sie weitere Informationen zu energiebegrenzten und damit aperiodischen Signalen, zu denen beispielsweise der [[Signaldarstellung/Einige_Sonderf%C3%A4lle_impulsartiger_Signale#Gau.C3.9Fimpuls|Gaußimpuls]] und der [[Aufgaben:3.1_Spektrum_des_Exponentialimpulses|Exponentialimpuls]] gehören. | + | *Aber auch zeitlich unbegrenzte Signale können durchaus eine endliche Energie besitzen. In späteren [[Signaldarstellung/Fouriertransformation_und_-rücktransformation|Kapiteln]] finden Sie weitere Informationen zu energiebegrenzten und damit aperiodischen Signalen, zu denen beispielsweise der [[Signaldarstellung/Einige_Sonderf%C3%A4lle_impulsartiger_Signale#Gau.C3.9Fimpuls|Gaußimpuls]] und der [[Aufgaben:3.1_Spektrum_des_Exponentialimpulses|Exponentialimpuls]] gehören. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Ein Signal $x(t)$ mit endlicher Leistung $P_x$ und dementsprechend unendlich großer Energie $(E_x \to \infty)$ bezeichnet man als '''leistungsbegrenzt'''.}} | + | Ein Signal $x(t)$ mit endlicher Leistung $P_x$ und dementsprechend unendlich großer Energie $(E_x \to \infty)$ bezeichnet man als '''leistungsbegrenzt'''.}} |
| − | *Alle leistungsbegrenzten Signale sind auch zeitlich unendlich weit ausgedehnt. Beispiele hierfür sind das [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals|Gleichsignal]] und [[Signaldarstellung/Harmonische_Schwingung|Harmonische Schwingungen]] wie das Cosinussignal $x_2(t)$ im $\text{Beispiel 3}$, die im Kapitel [[Signaldarstellung/Allgemeine_Beschreibung|Periodische Signale]] ausführlich beschrieben werden. | + | *Alle leistungsbegrenzten Signale sind auch zeitlich unendlich weit ausgedehnt. |
| − | *Auch die meisten stochastischen Signale sind leistungsbegrenzt – siehe Buch [[Stochastische Signaltheorie]]. | + | *Beispiele hierfür sind das [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals|Gleichsignal]] und [[Signaldarstellung/Harmonische_Schwingung|Harmonische Schwingungen]] wie das Cosinussignal $x_2(t)$ im $\text{Beispiel 3}$, die im Kapitel [[Signaldarstellung/Allgemeine_Beschreibung|Periodische Signale]] ausführlich beschrieben werden. |
| + | *Auch die meisten stochastischen Signale sind leistungsbegrenzt – siehe Buch [[Stochastische Signaltheorie]]. | ||
| Zeile 145: | Zeile 148: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Ein Signal bezeichnet man als '''wertkontinuierlich''', wenn der entscheidende Signalparameter – zum Beispiel der Augenblickswert – alle Werte eines Kontinuums (beispielsweise eines Intervalls) annehmen kann. Sind für den Signalparameter dagegen nur abzählbar viele verschiedene Werte möglich, so ist das Signal ''wertdiskret''. Die Anzahl der möglichen Werte bezeichnet man als die '''Stufenzahl''' $M$ | + | Ein Signal bezeichnet man als '''wertkontinuierlich''', wenn der entscheidende Signalparameter – zum Beispiel der Augenblickswert – alle Werte eines Kontinuums (beispielsweise eines Intervalls) annehmen kann. Sind für den Signalparameter dagegen nur abzählbar viele verschiedene Werte möglich, so ist das Signal ''wertdiskret''. Die Anzahl der möglichen Werte bezeichnet man als die '''Stufenzahl''' $M$ oder als den Werteumfang.}} |
| Zeile 155: | Zeile 158: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 4:}$ | $\text{Beispiel 4:}$ | ||
| − | Das obere Bild zeigt in blau einen Ausschnitt eines wertkontinuierlichen Signals $x(t)$, das Werte zwischen $\pm 8\ \rm V$ annehmen kann. | + | Das obere Bild zeigt in blau einen Ausschnitt eines wertkontinuierlichen Signals $x(t)$, das Werte zwischen $\pm 8\ \rm V$ annehmen kann. |
| − | *In roter Farbe erkennt man das auf $M = 8$ Quantisierungsstufen diskretisierte Signal $x_{\rm Q}(t)$ mit den möglichen Signalwerten $\pm 1\ \rm V$, $\pm 3\ \rm V$, $\pm 5\ \rm V$ und $\pm 7\ \rm V$. | + | *In roter Farbe erkennt man das auf $M = 8$ Quantisierungsstufen diskretisierte Signal $x_{\rm Q}(t)$ mit den möglichen Signalwerten $\pm 1\ \rm V$, $\pm 3\ \rm V$, $\pm 5\ \rm V$ und $\pm 7\ \rm V$. |
| − | *Bei diesem Signal $x_{\rm Q}(t)$ wurde der Augenblickswert als der entscheidende Signalparameter betrachtet. | + | *Bei diesem Signal $x_{\rm Q}(t)$ wurde der Augenblickswert als der entscheidende Signalparameter betrachtet. |
| Zeile 170: | Zeile 173: | ||
| − | Bei einem FSK-System (''Frequency Shift Keying'') ist dagegen die Augenblicksfrequenz der wesentliche Signalparameter. Deshalb bezeichnet man auch das unten dargestellte Signal $s_{\rm FSK}(t)$ als wertdiskret mit der Stufenzahl $M = 2$ und den möglichen Frequenzen $1 \ \rm kHz$ und $5 \ \rm kHz$, obwohl der Augenblickswert wertkontinuierlich ist.}} | + | Bei einem FSK-System (''Frequency Shift Keying'') ist dagegen die Augenblicksfrequenz der wesentliche Signalparameter. |
| + | |||
| + | Deshalb bezeichnet man auch das unten dargestellte Signal $s_{\rm FSK}(t)$ als wertdiskret mit der Stufenzahl $M = 2$ und den möglichen Frequenzen $1 \ \rm kHz$ und $5 \ \rm kHz$, obwohl der Augenblickswert wertkontinuierlich ist.}} | ||
==Zeitkontinuierliche und zeitdiskrete Signale== | ==Zeitkontinuierliche und zeitdiskrete Signale== | ||
<br> | <br> | ||
| − | Bei den bisher betrachteten Signalen war der Signalparameter zu jedem beliebigen Zeitpunkt definiert. Man spricht dann von einem ''zeitkontinuierlichen Signal''. | + | Bei den bisher betrachteten Signalen war der Signalparameter zu jedem beliebigen Zeitpunkt definiert. Man spricht dann von einem ''zeitkontinuierlichen Signal''. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Bei einem '''zeitdiskreten Signal''' ist im Gegensatz dazu der Signalparameter nur zu den diskreten Zeitpunkten $t_\nu$ definiert, wobei man diese Zeitpunkte meist äquidistant wählt: $t_\nu = \nu \cdot T_{\rm A}$. Da ein solches Signal beispielsweise durch Abtastung eines zeitkontinuierlichen Signals entsteht, bezeichnen wir $T_{\rm A}$ als den ''Abtastzeitabstand'' und dessen Kehrwert $f_{\rm A} = 1/T_{\rm A}$ als die ''Abtastfrequenz''.}} | + | Bei einem '''zeitdiskreten Signal''' ist im Gegensatz dazu der Signalparameter nur zu den diskreten Zeitpunkten $t_\nu$ definiert, wobei man diese Zeitpunkte meist äquidistant wählt: $t_\nu = \nu \cdot T_{\rm A}$. |
| + | |||
| + | Da ein solches Signal beispielsweise durch Abtastung eines zeitkontinuierlichen Signals entsteht, bezeichnen wir $T_{\rm A}$ als den ''Abtastzeitabstand'' und dessen Kehrwert $f_{\rm A} = 1/T_{\rm A}$ als die ''Abtastfrequenz''.}} | ||
| + | |||
| + | |||
| + | Weiter gilt: | ||
| + | *Ein zeitdiskretes Signal $x(t)$ ist durch die ''zeitliche Folge'' $\left \langle x_\nu \right \rangle$ ''seiner Abtastwerte'' vollständig bestimmt. | ||
| + | *Diese Abtastwerte können dabei sowohl wertkontinuierlich als auch wertdiskret sein. | ||
| + | *Die mathematische Beschreibung zeitdiskreter Signale erfolgt im Kapitel [[Signaldarstellung/Zeitdiskrete_Signaldarstellung|Zeitdiskrete Signaldarstellung]]. | ||
| Zeile 185: | Zeile 198: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 5:}$ | $\text{Beispiel 5:}$ | ||
| − | Das zeitdiskrete Signal $x_{\rm A}(t)$ erhält man nach Abtastung des oben dargestellten zeit- und wertkontinuierlichen Nachrichtensignals $x(t)$ im Abstand $T_{\rm A}$. | + | Das zeitdiskrete Signal $x_{\rm A}(t)$ erhält man nach Abtastung des oben dargestellten zeit- und wertkontinuierlichen Nachrichtensignals $x(t)$ im Abstand $T_{\rm A}$. |
| − | |||
| + | *Der unten skizzierte Zeitverlauf $x_{\rm R}(t)$ unterscheidet sich von der echten zeitdiskreten Darstellung $x_{\rm A}(t)$ dadurch, dass die unendlich schmalen Abtastwerte (mathematisch mit Diracimpulsen beschreibbar) durch Rechteckimpulse der Dauer $T_{\rm A}$ ersetzt sind. | ||
| − | + | ||
*Ein solches Signal kann nach obiger Definition ebenfalls als zeitdiskret bezeichnet werden.}} | *Ein solches Signal kann nach obiger Definition ebenfalls als zeitdiskret bezeichnet werden.}} | ||
| − | + | <br clear=all> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Analogsignale und Digitalsignale== | ==Analogsignale und Digitalsignale== | ||
<br> | <br> | ||
Version vom 22. August 2019, 15:02 Uhr
Inhaltsverzeichnis
Deterministische und stochastische Signale
In jedem Nachrichtensystem treten sowohl deterministische als auch stochastische Signale auf.
$\text{Definition:}$ Ein deterministisches Signal liegt vor, wenn dessen Zeitfunktionen $x(t)$ in analytischer Form vollständig angegeben werden kann.
Da hier die Zeitfunktion $x(t)$ für alle Zeiten $t$ bekannt und eindeutig angebbar ist, existiert für diese Signale stets eine über die Fourierreihe oder die Fouriertransformation berechenbare Spektralfunktion $X(f)$.
$\text{Definition:}$ Man spricht von einem stochastischen Signal bzw. von einem Zufallssignal, wenn der Signalverlauf $x(t)$ nicht – oder zumindest nicht vollständig – in mathematischer Form beschreibbar ist. Ein solches Signal kann für die Zukunft nicht exakt vorhergesagt werden.
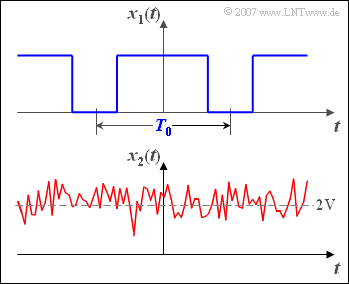
$\text{Beispiel 1:}$ Die Grafik zeigt Zeitverläufe eines deterministischen und eines stochastischen Signals:
- Oben ein periodisches Rechtecksignal $x_1(t)$ mit der Periodendauer $T_0$ ⇒ deterministisches Signal,
- unten ein Gaußsches Rauschsignal $x_2(t)$ mit dem Mittelwert $2\ \rm V $ ⇒ stochastisches Signal.
Für ein solches nichtdeterministisches Signal $x_2(t)$ ist daher auch keine Spektralfunktion $X_2(f)$ angebbar, da Fourierreihe/Fouriertransformation die genaue Kenntnis der Zeitfunktion für alle Zeiten $t$ voraussetzen.
Informationstragende Signale sind stets von stochastischer Art. Ihre Beschreibung sowie die Definition geeigneter Kenngrößen erfolgt im Buch Stochastische Signaltheorie.
Aber auch die deterministischen Signale haben eine große Bedeutung für die Nachrichtentechnik. Beispiele hierfür sind:
- Testsignale für den Entwurf von Nachrichtensystemen,
- Trägersignale für Frequenzmultiplexsysteme, und
- ein Puls zur Abtastung eines Analogsignals oder zur Zeitregenerierung eines Digitalsignals.
Kausale und akausale Signale
In der Nachrichtentechnik rechnet man oftmals mit zeitlich unbegrenzten Signalen; der Definitionsbereich des Signals erstreckt sich dann von $t = -\infty$ bis $t=+\infty$.
In der Realität gibt es allerdings solche Signale nicht, denn jedes Signal musste irgendwann einmal eingeschaltet werden. Wählt man – zwar willkürlich, aber dennoch sinnvoll – den Einschaltzeitpunkt $t = 0$, so kommt man zu folgender Klassifizierung:
$\text{Definition:}$ Man bezeichnet ein Signal $x(t)$ als kausal, wenn es für alle Zeiten $t < 0$ nicht existiert bzw. identisch Null ist. Ist diese Bedingung nicht erfüllt, so liegt ein akausales Signal (oder System) vor.
In vorliegenden Buch „Signaldarstellung” werden meist akausale Signale und Systeme betrachtet. Dies hat folgende Gründe:
- Akausale Signale (und Systeme) sind mathematisch leichter zu handhaben als kausale. Beispielsweise kann man hier die Spektralfunktion mittels Fouriertansformation bestimmen und man benötigt nicht wie bei der Laplacetransformation weitreichende Kenntnisse der Funktionentheorie.
- Akausale Signale und Systeme beschreiben den Sachverhalt vollständig und richtig, wenn man die Problematik des Einschaltvorgangs außer Acht lässt und sich somit nur für den eingeschwungenen Zustand interessiert.
Die Beschreibung kausaler Signale und Systeme mit Hilfe der Laplacetransformation folgt im Buch Lineare zeitinvariante Systeme.
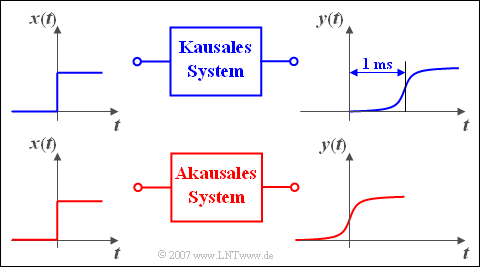
$\text{Beispiel 2:}$ Sie sehen in der oberen Grafik ein kausales Übertragungssystem:
- Wird an dessen Eingang eine Sprungfunktion $x(t)$ angelegt, so kann auch das Ausgangssignal $y(t)$ erst ab dem Zeitpunkt $t = 0$ von Null auf seinen Maximalwert ansteigen.
- Ansonsten wäre der Kausalzusammenhang, dass die Wirkung nicht vor der Ursache einsetzen kann, nicht erfüllt.
Im unteren Bild ist diese Kausalität nicht mehr gegeben. Wie leicht zu ersehen ist, kommt man bei diesem Beispiel schon durch eine zusätzliche Laufzeit von einer Millisekunde von der akausalen zur kausalen Darstellung.
Energiebegrenzte und leistungsbegrenzte Signale
An dieser Stelle müssen zunächst zwei wichtige Signalbeschreibungsgrößen eingeführt werden, nämlich die Energie und die Leistung.
- Im Sinne der Physik entspricht die Energie der Arbeit und hat zum Beispiel die Einheit „Ws“.
- Die Leistung ist als „Arbeit pro Zeit” definiert und besitzt somit die Einheit „W“.
Beide Größen sind nach den elementaren Gesetzen der Elektrotechnik vom Widerstand $R$ abhängig. Um diese Abhängigkeit zu eliminieren, wird in der Nachrichtentechnik oftmals der Widerstand $R=1 \,\Omega$ zugrunde gelegt. Dann gelten folgende Definitionen:
$\text{Definition:}$ Die Energie des Signals $x(t)$ ist wie folgt zu berechnen:
- $$E_x=\lim_{T_{\rm M}\to\infty} \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$
$\text{Definition:}$ Zur Berechnung der (mittleren) Leistung muss vor dem Grenzübergang noch durch die Zeit $T_{\rm M}$ dividiert werden:
- $$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M} } \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$
Hierbei bezeichnet $T_{\rm M}$ die symmetrisch bezüglich des Zeitursprungs $(t = 0)$ angenommene Messdauer, während der das Signal beobachtet wird. Dieses Zeitintervall muss im Allgemeinen sehr groß gewählt werden; im Idealfall sollte $T_{\rm M}$ gegen unendlich gehen.
Bezeichnet $x(t)$ einen Spannungsverlauf mit der Einheit $\text{V}$, so hat nach obigen Gleichungen
- die Signalenergie die Einheit $\text{V}^2\text{s}$,
- die Signalleistung die Einheit $\text{V}^2$.
Diese Aussage bedeutet auch: Bei den obigen Definitionen liegt bereits der Bezugswiderstand $R=1\,\Omega$ implizit zugrunde.
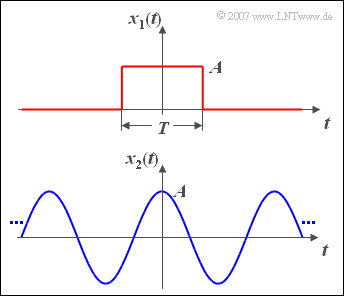
$\text{Beispiel 3:}$ Nun werden Energie und Leistung zweier beispielhafter Signale berechnet.
Die obere Grafik zeigt einen Rechteckimpuls $x_1(t)$ mit Amplitude $A$ und Dauer $T$.
- Die Signalenergie dieses Impulses ist $E_1 = A^2 \cdot T$.
- Für die Signalleistung ergibt sich aufgrund der Division durch $T_{\rm M}$ und Grenzwertbildung $(T_{\rm M} \to \infty)$ der Wert $P_1 = 0$.
Beim Cosinussignal $x_2(t)$ mit der Amplitude $A$ entsprechend der unteren Skizze gilt:
- Die Signalleistung ist unabhängig von der Frequenz gleich $P_2 = A^2/2$.
- Die Signalenergie $E_2$ (Integral über die Leistung für alle Zeiten) ist unendlich.
Mit $A = 4 \ {\rm V}$ ergibt sich für die Leistung $P_2 = 8 \ {\rm V}^2$. Mit dem Widerstand von $R = 50 \,\,\Omega$ entspricht dies der physikalischen Leistung ${8}/{50} \,\,{\rm V}\hspace{-0.1cm}/{\Omega}= 160\,\, {\rm mW}$.
Entsprechend diesem Beispiel gibt es die folgenden Klassifizierungsmerkmale:
$\text{Definition:}$ Ein Signal $x(t)$ mit endlicher Energie $E_x$ und unendlich kleiner Leistung $(P_x = 0)$ bezeichnet man als energiebegrenzt.
- Impulsförmige Signale wie das Signal $x_1(t)$ im obigen Beispiel sind stets energiebegrenzt. Meist sind hier die Signalwerte nur für eine endliche Zeitdauer von Null verschieden. In anderen Worten: Solche Signale sind oft auch zeitbegrenzt.
- Aber auch zeitlich unbegrenzte Signale können durchaus eine endliche Energie besitzen. In späteren Kapiteln finden Sie weitere Informationen zu energiebegrenzten und damit aperiodischen Signalen, zu denen beispielsweise der Gaußimpuls und der Exponentialimpuls gehören.
$\text{Definition:}$ Ein Signal $x(t)$ mit endlicher Leistung $P_x$ und dementsprechend unendlich großer Energie $(E_x \to \infty)$ bezeichnet man als leistungsbegrenzt.
- Alle leistungsbegrenzten Signale sind auch zeitlich unendlich weit ausgedehnt.
- Beispiele hierfür sind das Gleichsignal und Harmonische Schwingungen wie das Cosinussignal $x_2(t)$ im $\text{Beispiel 3}$, die im Kapitel Periodische Signale ausführlich beschrieben werden.
- Auch die meisten stochastischen Signale sind leistungsbegrenzt – siehe Buch Stochastische Signaltheorie.
Wertkontinuierliche und wertdiskrete Signale
$\text{Definition:}$ Ein Signal bezeichnet man als wertkontinuierlich, wenn der entscheidende Signalparameter – zum Beispiel der Augenblickswert – alle Werte eines Kontinuums (beispielsweise eines Intervalls) annehmen kann. Sind für den Signalparameter dagegen nur abzählbar viele verschiedene Werte möglich, so ist das Signal wertdiskret. Die Anzahl der möglichen Werte bezeichnet man als die Stufenzahl $M$ oder als den Werteumfang.
- Bei den analogen Übertragungssystemen wird stets mit wertkontinuierlichen Signalen gearbeitet.
- Bei Digitalsystemen sind dagegen die meisten Signale – aber nicht alle – wertdiskret.
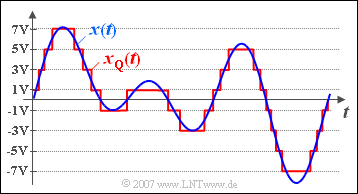
$\text{Beispiel 4:}$ Das obere Bild zeigt in blau einen Ausschnitt eines wertkontinuierlichen Signals $x(t)$, das Werte zwischen $\pm 8\ \rm V$ annehmen kann.
- In roter Farbe erkennt man das auf $M = 8$ Quantisierungsstufen diskretisierte Signal $x_{\rm Q}(t)$ mit den möglichen Signalwerten $\pm 1\ \rm V$, $\pm 3\ \rm V$, $\pm 5\ \rm V$ und $\pm 7\ \rm V$.
- Bei diesem Signal $x_{\rm Q}(t)$ wurde der Augenblickswert als der entscheidende Signalparameter betrachtet.
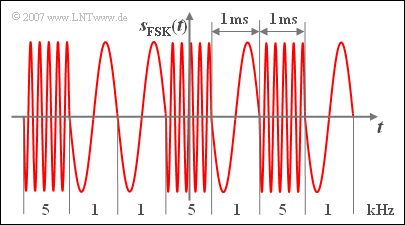
Bei einem FSK-System (Frequency Shift Keying) ist dagegen die Augenblicksfrequenz der wesentliche Signalparameter.
Deshalb bezeichnet man auch das unten dargestellte Signal $s_{\rm FSK}(t)$ als wertdiskret mit der Stufenzahl $M = 2$ und den möglichen Frequenzen $1 \ \rm kHz$ und $5 \ \rm kHz$, obwohl der Augenblickswert wertkontinuierlich ist.
Zeitkontinuierliche und zeitdiskrete Signale
Bei den bisher betrachteten Signalen war der Signalparameter zu jedem beliebigen Zeitpunkt definiert. Man spricht dann von einem zeitkontinuierlichen Signal.
$\text{Definition:}$ Bei einem zeitdiskreten Signal ist im Gegensatz dazu der Signalparameter nur zu den diskreten Zeitpunkten $t_\nu$ definiert, wobei man diese Zeitpunkte meist äquidistant wählt: $t_\nu = \nu \cdot T_{\rm A}$.
Da ein solches Signal beispielsweise durch Abtastung eines zeitkontinuierlichen Signals entsteht, bezeichnen wir $T_{\rm A}$ als den Abtastzeitabstand und dessen Kehrwert $f_{\rm A} = 1/T_{\rm A}$ als die Abtastfrequenz.
Weiter gilt:
- Ein zeitdiskretes Signal $x(t)$ ist durch die zeitliche Folge $\left \langle x_\nu \right \rangle$ seiner Abtastwerte vollständig bestimmt.
- Diese Abtastwerte können dabei sowohl wertkontinuierlich als auch wertdiskret sein.
- Die mathematische Beschreibung zeitdiskreter Signale erfolgt im Kapitel Zeitdiskrete Signaldarstellung.
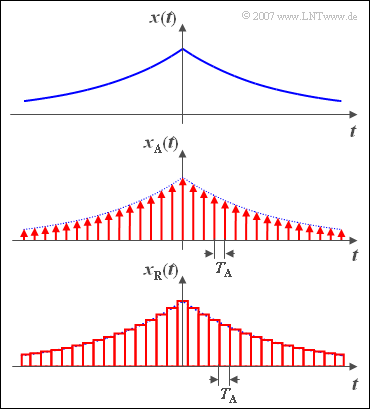
$\text{Beispiel 5:}$ Das zeitdiskrete Signal $x_{\rm A}(t)$ erhält man nach Abtastung des oben dargestellten zeit- und wertkontinuierlichen Nachrichtensignals $x(t)$ im Abstand $T_{\rm A}$.
- Der unten skizzierte Zeitverlauf $x_{\rm R}(t)$ unterscheidet sich von der echten zeitdiskreten Darstellung $x_{\rm A}(t)$ dadurch, dass die unendlich schmalen Abtastwerte (mathematisch mit Diracimpulsen beschreibbar) durch Rechteckimpulse der Dauer $T_{\rm A}$ ersetzt sind.
- Ein solches Signal kann nach obiger Definition ebenfalls als zeitdiskret bezeichnet werden.
Analogsignale und Digitalsignale
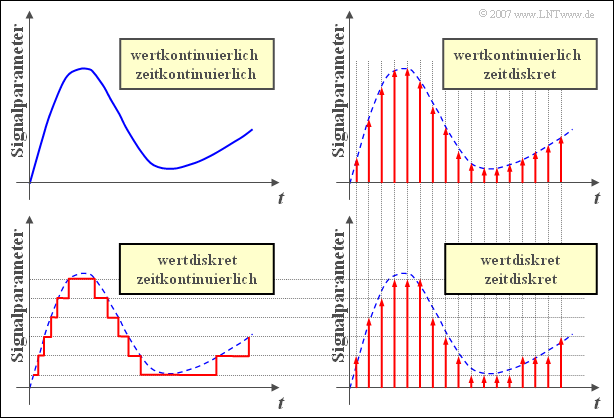
$\text{Beispiel 6:}$ In der folgenden Grafik sind noch einmal an einem Beispiel verdeutlicht die Signaleigenschaften
- „wertkontinuierlich” und „wertdiskret”, sowie
- „zeitkontinuierlich” und „zeitdiskret”.
Daneben gelten noch folgende Festlegungen:
$\text{Definition:}$ Ist ein Signal sowohl wert– als auch zeitkontinuierlich, so spricht man auch von einem Analogsignal. Solche Signale bilden einen kontinuierlichen Vorgang kontinuierlich ab. Beispiele hierfür sind Sprach–, Musik–, Bild– und Messsignale.
$\text{Definition:}$ Ein Digitalsignal ist dagegen stets wert- und zeitdiskret und die darin enthaltene Nachricht besteht aus den Symbolen eines Symbolvorrats. Es kann beispielsweise ein abgetastetes und quantisiertes (sowie in irgendeiner Form codiertes) Sprach–, Musik– oder Bildsignal sein, aber auch ein Datensignal, wenn im Internet eine Datei von einem Server heruntergeladen wird.
Je nach Stufenzahl sind Digitalsignale auch noch unter anderen Namen bekannt, beispielsweise
- mit $M = 2$: binäres Digitalsignal oder Binärsignal,
- mit $M = 3$: ternäres Digitalsignal oder Ternärsignal,
- mit $M = 4$: quaternäres Digitalsignal oder Quaternärsignal.
Das Lernvideo Analoge und digitale Signale fasst die hier behandelten Klassifizierungsmerkmale zusammen.
Aufgaben zum Kapitel
Aufgabe 1.2: Signalklassifizierung
Aufgabe 1.2Z: Pulscodemodulation