Applets:Diskrete Fouriertransformation und Inverse: Unterschied zwischen den Versionen
| Zeile 236: | Zeile 236: | ||
::* Im zweiten Fall ⇒ ${\rm Re}\big [d(\nu=1)] = 1$ ergibt sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit negativem Vorzeichen. | ::* Im zweiten Fall ⇒ ${\rm Re}\big [d(\nu=1)] = 1$ ergibt sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit negativem Vorzeichen. | ||
::* Für ${\rm Re}\big [d(\nu=15)] = 1$ würde sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit positivem Vorzeichen ergeben. | ::* Für ${\rm Re}\big [d(\nu=15)] = 1$ würde sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit positivem Vorzeichen ergeben. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(12)''' Neue Einstellung: $\text{DFT von (k) Dreieckimpuls}$. Interpretieren Sie die $d(\nu)$–Belegung und das DFT–Ergebnis.}} | ||
| + | |||
| + | ::* Wählen Sie die Betragsdarstellung. $x(t)$ ist symmetrisch um $t=0$ und erstreckt sich von $-T/2$ bis $+T/2$. Es gilt $T_{\rm A} = T/16$. $d(\nu)$–Belegung: | ||
| + | ::* $d(0)=x(0)= 1$, $d(1)=x(T_{\rm A})= 0.875$, ... , $d(8)=x(8T_{\rm A})= 0$, $d(9)=x(-7T_{\rm A})= 0.125$, ..., $d(15)=x(-T_{\rm A})= 0.875$. | ||
| + | ::* Im Frequenzbereich: Erst der Gleichanteil ⇒ $D(0)$, dann positive Frequenzen ⇒ $D(1) ,\text{...},D(8)$, dann negative Frequenzen (gespiegelt) ⇒ $D(9), \text{...},D(15)$. | ||
Version vom 1. September 2019, 15:30 Uhr
!!! Diese App wird gerade entwickelt. Entwicklungsstufe 0. Hat mit dem angekündigten Thema noch nichts zu tun!!!
Inhaltsverzeichnis
Programmbeschreibung
Das Applet verdeutlicht die Eigenschaften zweidimensionaler Gaußscher Zufallsgrößen $XY\hspace{-0.1cm}$, gekennzeichnet durch die Standardabweichungen (Streuungen) $\sigma_X$ und $\sigma_Y$ ihrer beiden Komponenten sowie den Korrelationskoeffizienten $\rho_{XY}$ zwischen diesen. Die Komponenten werden als mittelwertfrei vorausgesetzt: $m_X = m_Y = 0$.
Das Applet zeigt
- die zweidimensionale Wahrscheinlichkeitsdichtefunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{XY}(x, \hspace{0.1cm}y)$ in dreidimensionaler Darstellung sowie in Form von Höhenlinien,
- die zugehörige Randwahrscheinlichkeitsdichtefunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{X}(x)$ der Zufallsgröße $X$ als blaue Kurve; ebenso $f_{Y}(y)$ für die zweite Zufallsgröße,
- die zweidimensionale Verteilungsfunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{XY}(x, \hspace{0.1cm}y)$ als 3D-Plot,
- die Verteilungsfunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{X}(x)$ der Zufallsgröße $X$; ebenso $F_{Y}(y)$ als rote Kurve.
Das Applet verwendet das Framework Plot.ly
Theoretischer Hintergrund
Verbundwahrscheinlichkeitsdichtefunktion ⇒ 2D–WDF
Wir betrachten zwei wertkontinuierliche Zufallsgrößen $X$ und $Y\hspace{-0.1cm}$, zwischen denen statistische Abhängigkeiten bestehen können. Zur Beschreibung der Wechselbeziehungen zwischen diesen Größen ist es zweckmäßig, die beiden Komponenten zu einer zweidimensionalen Zufallsgröße $XY =(X, Y)$ zusammenzufassen. Dann gilt:
$\text{Definition:}$ Die Verbundwahrscheinlichkeitsdichtefunktion ist die Wahrscheinlichkeitsdichtefunktion (WDF, englisch: Probability Density Function, kurz: PDF) der zweidimensionalen Zufallsgröße $XY$ an der Stelle $(x, y)$:
- $$f_{XY}(x, \hspace{0.1cm}y) = \lim_{\left.{\Delta x\rightarrow 0 \atop {\Delta y\rightarrow 0} }\right.}\frac{ {\rm Pr}\big [ (x - {\rm \Delta} x/{\rm 2} \le X \le x + {\rm \Delta} x/{\rm 2}) \cap (y - {\rm \Delta} y/{\rm 2} \le Y \le y +{\rm \Delta}y/{\rm 2}) \big] }{ {\rm \Delta} \ x\cdot{\rm \Delta} y}.$$
- Die Verbundwahrscheinlichkeitsdichtefunktion oder kurz $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ ist eine Erweiterung der eindimensionalen WDF.
- $∩$ kennzeichnet die logische UND-Verknüpfung.
- $X$ und $Y$ bezeichnen die beiden Zufallsgrößen, und $x \in X$ sowie $y \in Y$ geben Realisierungen hiervon an.
- Die für dieses Applet verwendete Nomenklatur unterscheidet sich also geringfügig gegenüber der Beschreibung im Theorieteil.
Anhand dieser 2D–WDF $f_{XY}(x, y)$ werden auch statistische Abhängigkeiten innerhalb der zweidimensionalen Zufallsgröße $XY$ vollständig erfasst im Gegensatz zu den beiden eindimensionalen Dichtefunktionen ⇒ Randwahrscheinlichkeitsdichtefunktionen:
- $$f_{X}(x) = \int _{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}y ,$$
- $$f_{Y}(y) = \int_{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}x .$$
Diese beiden Randdichtefunktionen $f_X(x)$ und $f_Y(y)$
- liefern lediglich statistische Aussagen über die Einzelkomponenten $X$ bzw. $Y$,
- nicht jedoch über die Bindungen zwischen diesen.
Als quantitatives Maß für die linearen statistischen Bindungen ⇒ Korrelation verwendet man
- die Kovarianz $\mu_{XY}$, die bei mittelwertfreien Komponenten gleich dem gemeinsamen linearen Moment erster Ordnung ist:
- $$\mu_{XY} = {\rm E}\big[X \cdot Y\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} X \cdot Y \cdot f_{XY}(x,y) \,{\rm d}x \, {\rm d}y ,$$
- den Korrelationskoeffizienten nach Normierung auf die beiden Effektivwerte $σ_X$ und $σ_Y$ der beiden Komponenten:
- $$\rho_{XY}=\frac{\mu_{XY} }{\sigma_X \cdot \sigma_Y}.$$
$\text{Eigenschaften des Korrelationskoeffizienten:}$
- Aufgrund der Normierung gilt stets $-1 \le ρ_{XY} ≤ +1$.
- Sind die beiden Zufallsgrößen $X$ und $Y$ unkorreliert, so ist $ρ_{XY} = 0$.
- Bei strenger linearer Abhängigkeit zwischen $X$ und $Y$ ist $ρ_{XY}= ±1$ ⇒ vollständige Korrelation.
- Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $X$–Wert im statistischen Mittel auch $Y$ größer ist als bei kleinerem $X$.
- Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $Y$ mit steigendem $X$ im Mittel kleiner wird.
2D–WDF bei Gaußschen Zufallsgrößen
Für den Sonderfall Gaußscher Zufallsgrößen – der Name geht auf den Wissenschaftler Carl Friedrich Gauß zurück – können wir weiterhin vermerken:
- Die Verbund–WDF einer Gaußschen 2D-Zufallsgröße $XY$ mit Mittelwerten $m_X = 0$ und $m_Y = 0$ sowie dem Korrelationskoeffizienten $ρ = ρ_{XY}$ lautet:
- $$f_{XY}(x,y)=\frac{\rm 1}{\rm 2\it\pi \cdot \sigma_X \cdot \sigma_Y \cdot \sqrt{\rm 1-\rho^2}}\ \cdot\ \exp\Bigg[-\frac{\rm 1}{\rm 2 \cdot (1-\it\rho^{\rm 2} {\rm)}}\cdot(\frac {\it x^{\rm 2}}{\sigma_X^{\rm 2}}+\frac {\it y^{\rm 2}}{\sigma_Y^{\rm 2}}-\rm 2\it\rho\cdot\frac{x \cdot y}{\sigma_x \cdot \sigma_Y}\rm ) \rm \Bigg]\hspace{0.8cm}{\rm mit}\hspace{0.5cm}-1 \le \rho \le +1.$$
- Ersetzt man $x$ durch $(x - m_X)$ sowie $y$ durch $(y- m_Y)$, so ergibt sich die allgemeinere WDF einer zweidimensionalen Gaußschen Zufallsgröße mit Mittelwert.
- Die Randwahrscheinlichkeitsdichtefunktionen $f_{X}(x)$ und $f_{Y}(y)$ einer Gaußschen 2D-Zufallsgröße sind ebenfalls gaußförmig mit den Streuungen $σ_X$ bzw. $σ_Y$.
- Bei unkorrelierten Komponenten $X$ und $Y$ muss in obiger Gleichung $ρ = 0$ eingesetzt werden, und man erhält dann das Ergebnis:
- $$f_{XY}(x,y)=\frac{1}{\sqrt{2\pi}\cdot\sigma_{X}} \cdot\rm e^{-\it {x^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\hspace{0.05cm}\it\sigma_{X}^{\rm 2}} {\rm )}} \cdot\frac{1}{\sqrt{2\pi}\cdot\sigma_{\it Y}}\cdot e^{-\it {y^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\hspace{0.05cm}\it\sigma_{Y}^{\rm 2}} {\rm )}} = \it f_{X} \rm ( \it x \rm ) \cdot \it f_{Y} \rm ( \it y \rm ) .$$
$\text{Fazit:}$ Im Sonderfall einer 2D-Zufallsgröße mit Gaußscher WDF $f_{XY}(x, y)$ folgt aus der Unkorreliertheit auch direkt die statistische Unabhängigkeit:
- $$f_{XY}(x,y)= f_{X}(x) \cdot f_{Y}(y) . $$
Bitte beachten Sie:
- Bei keiner anderen WDF kann aus der Unkorreliertheit auf die statistische Unabhängigkeit geschlossen werden.
- Man kann aber stets ⇒ für jede beliebige 2D–WDF $f_{XY}(x, y)$ von der statistischen Unabhängigkeit auf die Unkorreliertheit schließen, weil:
- Sind zwei Zufallsgrößen $X$ und $Y$ völlig voneinander (statistisch) unabhängig, so gibt es zwischen ihnen natürlich auch keine linearen Abhängigkeiten
⇒ sie sind dann auch unkorreliert ⇒ $ρ = 0$.
Höhenlinien bei unkorrelierten Zufallsgrößen
Aus der Bedingungsgleichung $f_{XY}(x, y) = {\rm const.}$ können die Höhenlinien der WDF berechnet werden.
Sind die Komponenten $X$ und $Y$ unkorreliert $(ρ_{XY} = 0)$, so erhält man als Gleichung für die Höhenlinien:
- $$\frac{x^{\rm 2}}{\sigma_{X}^{\rm 2}}+\frac{y^{\rm 2}}{\sigma_{Y}^{\rm 2}} =\rm const.$$
Die Höhenlinien beschreiben in diesem Fall folgende Figuren:
- Kreise (falls $σ_X = σ_Y$, grüne Kurve), oder
- Ellipsen (für $σ_X ≠ σ_Y$, blaue Kurve) in Ausrichtung der beiden Achsen.
Korrelationsgerade
Als Korrelationsgerade bezeichnet man die Gerade $y = K(x)$ in der $(x, y)$–Ebene durch den „Mittelpunkt” $(m_X, m_Y)$. Diese besitzt folgende Eigenschaften:
- Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Messpunkte gemittelt – ist minimal:
- $$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$
- Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet im allgemeinen Fall:
- $$y=K(x)=\frac{\sigma_Y}{\sigma_X}\cdot\rho_{XY}\cdot(x - m_X)+m_Y.$$
- Der Winkel, den die Korrelationsgerade zur $x$–Achse einnimmt, beträgt:
- $$\theta={\rm arctan}(\frac{\sigma_{Y} }{\sigma_{X} }\cdot \rho_{XY}).$$
Höhenlinien bei korrelierten Zufallsgrößen
Bei korrelierten Komponenten $(ρ_{XY} ≠ 0)$ sind die Höhenlinien der WDF (fast) immer elliptisch, also auch für den Sonderfall $σ_X = σ_Y$.
Ausnahme: $ρ_{XY}=\pm 1$ ⇒ Diracwand; siehe Aufgabe 4.4 im Buch „Stochastische Signaltheorie”, Teilaufgabe (5).
Hier lautet die Bestimmungsgleichung der WDF-Höhenlinien:
- $$f_{XY}(x, y) = {\rm const.} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \frac{x^{\rm 2} }{\sigma_{X}^{\rm 2}}+\frac{y^{\rm 2} }{\sigma_{Y}^{\rm 2} }-{\rm 2}\cdot\rho_{XY}\cdot\frac{x\cdot y}{\sigma_X\cdot \sigma_Y}={\rm const.}$$
Die Grafik zeigt in hellerem Blau für zwei unterschiedliche Parametersätze je eine Höhenlinie.
- Die Ellipsenhauptachse ist dunkelblau gestrichelt.
- Die Korrelationsgerade $K(x)$ ist durchgehend rot eingezeichnet.
Anhand dieser Darstellung sind folgende Aussagen möglich:
- Die Ellipsenform hängt außer vom Korrelationskoeffizienten $ρ_{XY}$ auch vom Verhältnis der beiden Streuungen $σ_X$ und $σ_Y$ ab.
- Der Neigungswinkel $α$ der Ellipsenhauptachse (gestrichelte Gerade) gegenüber der $x$–Achse hängt ebenfalls von $σ_X$, $σ_Y$ und $ρ_{XY}$ ab:
- $$\alpha = {1}/{2} \cdot {\rm arctan } \big ( 2 \cdot \rho_{XY} \cdot \frac {\sigma_X \cdot \sigma_Y}{\sigma_X^2 - \sigma_Y^2} \big ).$$
- Die (rote) Korrelationsgerade $y = K(x)$ einer Gaußschen 2D–Zufallsgröße liegt stets unterhalb der (blau gestrichelten) Ellipsenhauptachse.
- $K(x)$ kann aus dem Schnittpunkt der Höhenlinien und ihrer vertikalen Tangenten geometrisch konstruiert werden, wie in der Skizze in grüner Farbe angedeutet.
Zweidimensionale Verteilungsfunktion ⇒ 2D–VTF
$\text{Definition:}$ Die 2D-Verteilungsfunktion ist ebenso wie die 2D-WDF lediglich eine sinnvolle Erweiterung der eindimensionalen Verteilungsfunktion (VTF):
- $$F_{XY}(x,y) = {\rm Pr}\big [(X \le x) \cap (Y \le y) \big ] .$$
Es ergeben sich folgende Gemeinsamkeiten und Unterschiede zwischen der „1D-VTF” und der„ 2D-VTF”:
- Der Funktionalzusammenhang zwischen „2D–WDF” und „2D–VTF” ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt:
- $$F_{XY}(x,y)=\int_{-\infty}^{y} \int_{-\infty}^{x} f_{XY}(\xi,\eta) \,\,{\rm d}\xi \,\, {\rm d}\eta .$$
- Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $x$ und $y$ angeben:
- $$f_{XY}(x,y)=\frac{{\rm d}^{\rm 2} F_{XY}(\xi,\eta)}{{\rm d} \xi \,\, {\rm d} \eta}\Bigg|_{\left.{x=\xi \atop {y=\eta}}\right.}.$$
- Bezüglich der Verteilungsfunktion $F_{XY}(x, y)$ gelten folgende Grenzwerte:
- $$F_{XY}(-\infty,\ -\infty) = 0,\hspace{0.5cm}F_{XY}(x,\ +\infty)=F_{X}(x ),\hspace{0.5cm} F_{XY}(+\infty,\ y)=F_{Y}(y ) ,\hspace{0.5cm}F_{XY}(+\infty,\ +\infty) = 1.$$
- Im Grenzfall $($unendlich große $x$ und $y)$ ergibt sich demnach für die „2D-VTF” der Wert $1$. Daraus erhält man die Normierungsbedingung für die 2D-Wahrscheinlichkeitsdichtefunktion:
- $$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$
$\text{Fazit:}$ Beachten Sie den signifikanten Unterschied zwischen eindimensionalen und zweidimensionalen Zufallsgrößen:
- Bei eindimensionalen Zufallsgrößen ergibt die Fläche unter der WDF stets den Wert $1$.
- Bei zweidimensionalen Zufallsgrößen ist das WDF-Volumen immer gleich $1$.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Bei der Aufgabenbeschreibung verwenden wir $\rho$ anstelle von $\rho_{XY}$.
- Für die „1D-WDF” gilt: $f_{X}(x) = \sqrt{1/(2\pi \cdot \sigma_X^2)} \cdot {\rm e}^{-x^2/(2 \hspace{0.05cm}\cdot \hspace{0.05cm} \sigma_X^2)}$.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
(1) Neue Einstellung: $\text{DFT von Signal (a): Gleichsignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen FT?
- Im Zeitbereich sind alle $d(\nu) =1$. Dann sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(0)] =1$.
- Dies entspricht bei der herkömmlichen (zeitkontinuierlichen) Fouriertransformation: $x(t) = A\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = A \cdot \delta(f=0)$ mit $A=1$.
(2) Gehen Sie vom erhaltenen $D(\mu)$–Feld aus und verschieben Sie alle Koeffizienten um eine Stelle nach unten. Welche Zeitfunktion liefert die $\rm IDFT$?
- Nun sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Das Zeitbereichsergebnis ist eine komplexe Exonentialfunktion.
- Der Realteil des $d(\nu)$–Feldes zeigt einen Cosinus und der Imaginärteil eine Sinusfunktion. Bei beiden Funktionen erkennt man jeweils eine Periode.
(3) Ergänzen Sie das aktuelle $D(\mu)$–Feld um den Koeffizienten ${\rm Im}\big [D(1)] =1$. Welche Unterschiede erkennt man gegenüber (2) im Zeitbereich?
- Zum einen erkennt man nun bei Realteil und Imaginärteil eine Phasenverschiebung um zwei Stützwerte. Dies entspricht der Phase $\varphi = 45^\circ$.
- Zudem wurden die Amplituden von Real– und Imaginärteil jeweils um den Faktor $\sqrt{2}$ vergrößert.
(4) Setzen Sie das $D(\mu)$–Feld auf Null mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Durch welchen zusätzlichen $D(\mu)$–Koeffizienten erhält man ein reelles $d(\nu)$–Feld?
- Durch Probieren oder Nachdenken erkennt man, dass auch ${\rm Re}\big [D(15)] =1$ gesetzt werden muss. Dann beschreibt das $d(\nu)$–Feld einen Cosinus.
- Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = 2 \cdot \cos(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = \delta(f -f_0)+\delta(f +f_0)$.
- Das Feld $D(1)$ steht für die Frequenz $f_0$ und aufgrund der Periodizät mit $N=16$ wird die Frequenz $-f_0$ durch $D(15) = D(-1)$ ausgedrückt.
(5) Mit welchem $D(\mu)$–Feld erhält man nach der $\rm IDFT$ im $d(\nu)$–Feld eine reelle Cosinusfunktion mit der Amplitude $A=1$?
- Die Diskrete Fouriertransformation ist ebenso wie die herkömmliche Fouriertransformation linear ⇒ $D(1) = D(15)=0.5$.
(6) Neue Einstellung: $\text{DFT von Signal (e): Cosinussignal}$ und anschließende Signalverschiebungen. Was bewirken diese Verschiebungen im Frequenzbereich?
- Eine Verschiebung im Zeitbereich verändert das Cosinussignal zu einer „Harmonischen Schwingung” mit beliebiger Phase.
- Das $D(\mu)$–Feld ist weiterhin Null bis auf $D(1)$ und $D(15)$. Die Beträge $|D(1)|$ und $|D(15)|$ bleiben ebenfalls gleich.
- Die alleinige Veränderung betrifft die Phase, also die unterschiedliche Aufteilung der Beträge auf Real– und Imaginärteil.
(7) Neue Einstellung: $\text{DFT von Signal (f): Sinussignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen FT?
- Das Sinussignal ergibt sich aus dem Cosinussignal durch vier Zeitverschiebungen. Deshalb gelten alle Aussagen von (6) weiterhin.
- Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = \sin(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = {\rm j}/2 \cdot \big [\delta(f +f_0)-\delta(f -f_0)\big ]$.
- Der Koeffizient $D(1)$ ⇒ $($Frequenz: $+f_0)$ ist imaginär und hat den Imaginärteil $-0.5$. Entsprechend gilt ${\rm Im}\big [D(15)] =+0.5$ ⇒ $($Frequenz: $-f_0)$.
(8) Neue Einstellung: $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$. Interpretieren Sie das Ergebnis im Vergleich zur Aufgabe (5).
- Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (2f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -2 f_0)+0.5 \cdot \delta(f +2f_0)$.
- Für die Frequenz $2f_0$ steht das Feld $D(2)$ und für die Frequenz $-2f_0$ aufgrund der Periodizät das Feld $D(14) = D(-2)$ : $D(2) = D(14) = 0.5$.
(9) Untersuchen Sie nun den Fall $\text{DFT von Sinussignal (zwei Perioden)}$. Welche Einstellung müssen Sie vornehmen? Interpretieren Sie das Ergebnis.
- Zum gewünschten Signal kommt man von $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$ mit zwei Verschiebungen. Bei (7): Vier Verschiebungen.
- Das DFT–Ergebnis lautet dementsprechend: ${\rm Im}\big [D(2)] =-0.5$ und ${\rm Im}\big [D(14)] =+0.5$.
(10) Neue Einstellung: $\text{DFT von (h) Alternierende Zeitkoeffizienten}$. Interpretieren Sie das DFT–Ergebnis.
- Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (8f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -8 f_0)+0.5 \cdot \delta(f +8f_0)$.
- $8f_0$ ist die höchste mit $N=16$ in der DFT darstellbare Frequenz. Pro Periodendauer gibt es nur zwei Abtastwerte, nämlich $+1$ und $-1$.
- Unterschied zur Teilaufgabe (5): Aus $D(1) =0.5$ wird nun $D(8) =0.5$. Ebenso verschiebt sich $D(15) =0.5$ auf $D(8) =0.5$. Endergebnis: $D(8) =1$.
(11) Welche Unterschiede erhält man mit den beiden Einstellungen $\text{IDFT von Spektrum (C)}$ sowie $\text{DFT von Signal (c)}$ ?
- Im ersten Fall ⇒ ${\rm Re}\big [D(\mu=1)] = 1$ ergibt sich im Zeitbereich die komplexe Exponentialfunktion ⇒ $x(t) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_0 \hspace{0.05cm}\cdot\hspace{0.05cm} t}$ mit positivem Vorzeichen.
- Im zweiten Fall ⇒ ${\rm Re}\big [d(\nu=1)] = 1$ ergibt sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit negativem Vorzeichen.
- Für ${\rm Re}\big [d(\nu=15)] = 1$ würde sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit positivem Vorzeichen ergeben.
(12) Neue Einstellung: $\text{DFT von (k) Dreieckimpuls}$. Interpretieren Sie die $d(\nu)$–Belegung und das DFT–Ergebnis.
- Wählen Sie die Betragsdarstellung. $x(t)$ ist symmetrisch um $t=0$ und erstreckt sich von $-T/2$ bis $+T/2$. Es gilt $T_{\rm A} = T/16$. $d(\nu)$–Belegung:
- $d(0)=x(0)= 1$, $d(1)=x(T_{\rm A})= 0.875$, ... , $d(8)=x(8T_{\rm A})= 0$, $d(9)=x(-7T_{\rm A})= 0.125$, ..., $d(15)=x(-T_{\rm A})= 0.875$.
- Im Frequenzbereich: Erst der Gleichanteil ⇒ $D(0)$, dann positive Frequenzen ⇒ $D(1) ,\text{...},D(8)$, dann negative Frequenzen (gespiegelt) ⇒ $D(9), \text{...},D(15)$.
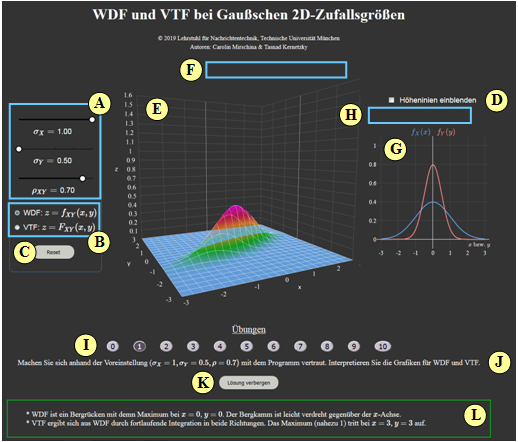
Zur Handhabung des Applets
(A) Parametereingabe per Slider: $\sigma_X$, $\sigma_Y$ und $\rho$
(B) Auswahl: Darstellung von WDF oder VTF
(C) Reset: Einstellung wie beim Programmstart
(D) Höhenlinien darstellen anstelle von „1D-WDF”
(E) Darstellungsbereich für „2D-WDF”
(F) Manipulation der 3D-Grafik (Zoom, Drehen, ...)
(G) Darstellungsbereich für „1D-WDF” bzw. „Höhenlinien”
(H) Manipulation der 2D-Grafik („1D-WDF”)
( I ) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(J) Bereich für die Versuchsdurchführung: Aufgabenstellung
(K) Bereich für die Versuchsdurchführung: Musterlösung einblenden
( L) Bereich für die Versuchsdurchführung: Musterlösung
Werte–Ausgabe über Maussteuerung (sowohl bei 2D als auch bei 3D)
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.