Signaldarstellung/Allgemeine Beschreibung: Unterschied zwischen den Versionen
| Zeile 59: | Zeile 59: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Ein '''periodisches Signal''' $x(t)$ liegt | + | Ein '''periodisches Signal''' $x(t)$ liegt dann vor, wenn für alle beliebigen Werte von $t$ und alle ganzzahligen Werte von $i$ mit einem geeigneten $T_{0}$ gilt: |
:$$x(t+i\cdot T_{0}) = x(t).$$}} | :$$x(t+i\cdot T_{0}) = x(t).$$}} | ||
| Zeile 65: | Zeile 65: | ||
Daraus ergeben sich die folgenden Kenngrößen: | Daraus ergeben sich die folgenden Kenngrößen: | ||
| − | *Die '''Periodendauer''' $T_{0}$ gibt den kleinstmöglichen Wert an, der obige Gleichung erfüllt. | + | *Die '''Periodendauer''' $T_{0}$ gibt den kleinstmöglichen Wert an, der obige Gleichung erfüllt. |
| − | *Die '''Grundfrequenz''' $f_{0} = 1/T_{0}$ beschreibt die Anzahl der Perioden pro Zeiteinheit (meist je Sekunde). | + | *Die '''Grundfrequenz''' $f_{0} = 1/T_{0}$ beschreibt die Anzahl der Perioden pro Zeiteinheit (meist je Sekunde). |
| − | *Die Einheit „1/s” wird auch mit „Hz” bezeichnet, benannt nach dem deutschen Physiker [https://de.wikipedia.org/wiki/Heinrich_Hertz Heinrich Hertz]. | + | *Die Einheit „1/s” wird auch mit „Hz” bezeichnet, benannt nach dem deutschen Physiker [https://de.wikipedia.org/wiki/Heinrich_Hertz Heinrich Hertz]. |
| − | *Die '''Grundkreisfrequenz''' $\omega_{0}$ stellt die Winkeldrehung pro Sekunde dar, die meistens im Bogenmaß angegeben wird. | + | *Die '''Grundkreisfrequenz''' $\omega_{0}$ stellt die Winkeldrehung pro Sekunde dar, die meistens im Bogenmaß angegeben wird. |
*Im Gegensatz zur Grundfrequenz ist hier nicht die Einheit „Hz”, sondern „1/s” üblich. Es gilt folgende Gleichung: | *Im Gegensatz zur Grundfrequenz ist hier nicht die Einheit „Hz”, sondern „1/s” üblich. Es gilt folgende Gleichung: | ||
:$$\omega_{0}=2\pi f_{0} = {2\pi}/{T_{0}}.$$ | :$$\omega_{0}=2\pi f_{0} = {2\pi}/{T_{0}}.$$ | ||
| Zeile 77: | Zeile 77: | ||
$\text{Beispiel 2:}$ | $\text{Beispiel 2:}$ | ||
Dargestellt ist hier ein periodisches Zeitsignal: | Dargestellt ist hier ein periodisches Zeitsignal: | ||
| − | *Die Periodendauer beträgt $T_{0} = 2.5 \ \rm ms$. | + | *Die Periodendauer beträgt $T_{0} = 2.5 \ \rm ms$. |
| − | *Daraus berechnet sich die Grundfrequenz $f_0 = 400 \ \rm Hz$. | + | *Daraus berechnet sich die Grundfrequenz $f_0 = 400 \ \rm Hz$. |
| − | *Die Grundkreisfrequenz ergibt sich zu $\omega_{0}=2513 \ \rm 1/s.$}} | + | *Die Grundkreisfrequenz ergibt sich zu $\omega_{0}=2513 \ \rm 1/s.$}} |
| Zeile 86: | Zeile 86: | ||
==Resultierende Periodendauer== | ==Resultierende Periodendauer== | ||
<br> | <br> | ||
| − | Besteht ein Signal $x(t)$ aus der Summe zweier periodischer Signale $x_{1}(t)$ und $x_{2}(t)$ mit den Periodendauern $T_{1}$ bzw. $T_{2}$, so ist die resultierende Periodendauer des Summensignals das kleinste gemeinsame Vielfache von $T_{1}$ und $T_{2}$. | + | Besteht ein Signal $x(t)$ aus der Summe zweier periodischer Signale $x_{1}(t)$ und $x_{2}(t)$ mit den Periodendauern $T_{1}$ bzw. $T_{2}$, so ist die resultierende Periodendauer des Summensignals das kleinste gemeinsame Vielfache von $T_{1}$ und $T_{2}$. |
*Diese Aussage gilt unabhängig von den Amplituden– und Phasenverhältnissen. | *Diese Aussage gilt unabhängig von den Amplituden– und Phasenverhältnissen. | ||
| − | *Besitzen $T_{1}$ und $T_{2}$ dagegen kein rationales gemeinsames Vielfaches (Beispiel: $T_{2} = \pi \cdot T_{1}$ | + | *Besitzen $T_{1}$ und $T_{2}$ dagegen kein rationales gemeinsames Vielfaches $($Beispiel: $T_{2} = \pi \cdot T_{1})$, so ist das Summensignal $x(t)$ im Gegensatz zu seinen beiden Komponenten $x_{1}(t)$ und $x_{2}(t)$ nicht periodisch. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 3:}$ | $\text{Beispiel 3:}$ | ||
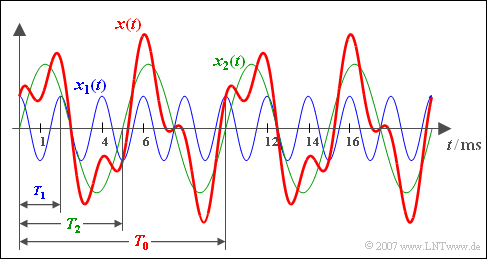
| − | Addiert werden ein cosinusförmiges Signal $x_{1}(t)$ mit der Periodendauer $T_{1} = 2\; {\rm ms}$ (blauer Signalverlauf) und ein Sinussignal $x_{2}(t)$ mit der Periodendauer $T_{2} = 5\; {\rm ms}$ und doppelt so großer Amplitude (grüner Verlauf). | + | Addiert werden ein cosinusförmiges Signal $x_{1}(t)$ mit der Periodendauer $T_{1} = 2\; {\rm ms}$ (blauer Signalverlauf) und ein Sinussignal $x_{2}(t)$ mit der Periodendauer $T_{2} = 5\; {\rm ms}$ und doppelt so großer Amplitude (grüner Verlauf). |
[[Datei:P_ID247__Sig_T_2_1_S3_neu.png|frame|Resultierende Periodendauer der Summe aus Cosinus– und Sinussignal]] | [[Datei:P_ID247__Sig_T_2_1_S3_neu.png|frame|Resultierende Periodendauer der Summe aus Cosinus– und Sinussignal]] | ||
| − | *Das (rote) Summensignal $x(t) = x_{1}(t) + x_{2}(t)$ weist dann die resultierende Periodendauer $T_{0} = 10\; {\rm ms}$ auf ⇒ Grundfrequenz $f_{0} = 100\; {\rm Hz}$. | + | *Das (rote) Summensignal $x(t) = x_{1}(t) + x_{2}(t)$ weist dann die resultierende Periodendauer $T_{0} = 10\; {\rm ms}$ auf ⇒ Grundfrequenz $f_{0} = 100\; {\rm Hz}$. |
| − | *Die Frequenz $f_{0}$ selbst ist in $x(t)$ nicht enthalten, lediglich ganzzahlige Vielfache davon, nämlich $f_{1} = 500\; {\rm Hz}$ und $f_{2} = 200\; {\rm Hz}$. }} | + | *Die Frequenz $f_{0}$ selbst ist in $x(t)$ nicht enthalten, lediglich ganzzahlige Vielfache davon, nämlich $f_{1} = 500\; {\rm Hz}$ und $f_{2} = 200\; {\rm Hz}$. }} |
| − | Mit dem interaktiven Applet [[Applets:Periodendauer_periodischer_Signale|Periodendauer periodischer Signale]] lässt sich die resultierende Periodendauer zweier harmonischer Schwingungen ermitteln. | + | Mit dem interaktiven Applet [[Applets:Periodendauer_periodischer_Signale|Periodendauer periodischer Signale]] lässt sich die resultierende Periodendauer zweier harmonischer Schwingungen ermitteln. |
Version vom 1. September 2019, 16:11 Uhr
Inhaltsverzeichnis
# ÜBERBLICK ZUM ZWEITEN HAUPTKAPITEL #
In diesem Kapitel werden periodische Signale betrachtet und diese sowohl im Zeit– als auch im Frequenzbereich mathematisch beschrieben.
Dieses Kapitel beinhaltet im Einzelnen:
- Einige Grundbegriffe wie Periodendauer, Grundfrequenz und Kreisfrequenz,
- die Eigenschaften eines Gleichsignals als Grenzfall eines periodischen Signals,
- die Definition und Interpretation der Diracfunktion,
- die Spektraldarstellung eines Gleichsignals oder eines Gleichsignalanteils,
- die Zeit– und Frequenzdarstellung harmonischer Schwingungen, und schließlich
- die Anwendung der Fourierreihe zur Spektralanalyse periodischer Signale.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 6: Lineare zeitinvariante Systeme (Programm lzi)
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese frühere LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms und
- dieser Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; Kapitel 6: Seite 99-118.
Eigenschaften und Anwendungen
Für die Nachrichtentechnik besitzen periodische Signale eine große Bedeutung:
- Sie gehören zur Klasse der deterministischen Signale, deren Zeitfunktion in analytischer Form angegeben werden kann.
- Ihr Signalverlauf ist damit für alle Zeiten $t$ bekannt und für die Zukunft eindeutig vorhersagbar.
- Sie sind daher niemals informationstragende Signale.
Trotzdem werden periodische Signale oft auch in der Nachrichtentechnik benötigt, zum Beispiel
- für die Modulation und Demodulation bei Trägerfrequenzsystemen,
- für die Synchronisation und Taktregenerierung bei Digitalsystemen,
- als Test– und Prüfsignale bei der Systemrealisierung.
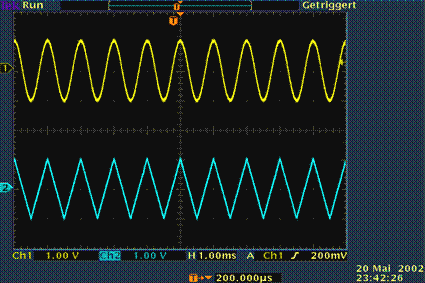
$\text{Beispiel 1:}$ Auf dem Oszilloskopbild sehen Sie zwei typische Vertreter periodischer Signale:
- oben ein Cosinussignal,
- unten ein Dreiecksignal.
Wie aus den eingeblendeten Einstellungen ersichtlich ist, beträgt bei beiden Signalen die Periodendauer eine Millisekunde und die Amplitude ein Volt.
Definition und Parameter
Bevor wir uns den Signalparametern eines periodischen Signals zuwenden, soll der Begriff „Periodizität” eindeutig definiert werden:
$\text{Definition:}$ Ein periodisches Signal $x(t)$ liegt dann vor, wenn für alle beliebigen Werte von $t$ und alle ganzzahligen Werte von $i$ mit einem geeigneten $T_{0}$ gilt:
- $$x(t+i\cdot T_{0}) = x(t).$$
Daraus ergeben sich die folgenden Kenngrößen:
- Die Periodendauer $T_{0}$ gibt den kleinstmöglichen Wert an, der obige Gleichung erfüllt.
- Die Grundfrequenz $f_{0} = 1/T_{0}$ beschreibt die Anzahl der Perioden pro Zeiteinheit (meist je Sekunde).
- Die Einheit „1/s” wird auch mit „Hz” bezeichnet, benannt nach dem deutschen Physiker Heinrich Hertz.
- Die Grundkreisfrequenz $\omega_{0}$ stellt die Winkeldrehung pro Sekunde dar, die meistens im Bogenmaß angegeben wird.
- Im Gegensatz zur Grundfrequenz ist hier nicht die Einheit „Hz”, sondern „1/s” üblich. Es gilt folgende Gleichung:
- $$\omega_{0}=2\pi f_{0} = {2\pi}/{T_{0}}.$$
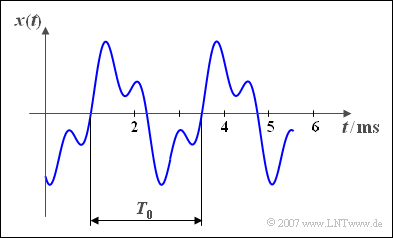
$\text{Beispiel 2:}$ Dargestellt ist hier ein periodisches Zeitsignal:
- Die Periodendauer beträgt $T_{0} = 2.5 \ \rm ms$.
- Daraus berechnet sich die Grundfrequenz $f_0 = 400 \ \rm Hz$.
- Die Grundkreisfrequenz ergibt sich zu $\omega_{0}=2513 \ \rm 1/s.$
Resultierende Periodendauer
Besteht ein Signal $x(t)$ aus der Summe zweier periodischer Signale $x_{1}(t)$ und $x_{2}(t)$ mit den Periodendauern $T_{1}$ bzw. $T_{2}$, so ist die resultierende Periodendauer des Summensignals das kleinste gemeinsame Vielfache von $T_{1}$ und $T_{2}$.
- Diese Aussage gilt unabhängig von den Amplituden– und Phasenverhältnissen.
- Besitzen $T_{1}$ und $T_{2}$ dagegen kein rationales gemeinsames Vielfaches $($Beispiel: $T_{2} = \pi \cdot T_{1})$, so ist das Summensignal $x(t)$ im Gegensatz zu seinen beiden Komponenten $x_{1}(t)$ und $x_{2}(t)$ nicht periodisch.
$\text{Beispiel 3:}$ Addiert werden ein cosinusförmiges Signal $x_{1}(t)$ mit der Periodendauer $T_{1} = 2\; {\rm ms}$ (blauer Signalverlauf) und ein Sinussignal $x_{2}(t)$ mit der Periodendauer $T_{2} = 5\; {\rm ms}$ und doppelt so großer Amplitude (grüner Verlauf).
- Das (rote) Summensignal $x(t) = x_{1}(t) + x_{2}(t)$ weist dann die resultierende Periodendauer $T_{0} = 10\; {\rm ms}$ auf ⇒ Grundfrequenz $f_{0} = 100\; {\rm Hz}$.
- Die Frequenz $f_{0}$ selbst ist in $x(t)$ nicht enthalten, lediglich ganzzahlige Vielfache davon, nämlich $f_{1} = 500\; {\rm Hz}$ und $f_{2} = 200\; {\rm Hz}$.
Mit dem interaktiven Applet Periodendauer periodischer Signale lässt sich die resultierende Periodendauer zweier harmonischer Schwingungen ermitteln.
Aufgaben zum Kapitel