Aufgaben:Aufgabe 2.3: Sinusförmige Kennlinie: Unterschied zwischen den Versionen
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID894__LZI_A_2_3.png|right|frame|Sinusförmige Kennlinie]] | [[Datei:P_ID894__LZI_A_2_3.png|right|frame|Sinusförmige Kennlinie]] | ||
| − | Wie betrachten ein System mit Eingang $x(t)$ und Ausgang $y(t)$. Zur einfacheren Darstellung werden die Signale als dimensionslos betrachtet. | + | Wie betrachten ein System mit Eingang $x(t)$ und Ausgang $y(t)$. Zur einfacheren Darstellung werden die Signale als dimensionslos betrachtet. |
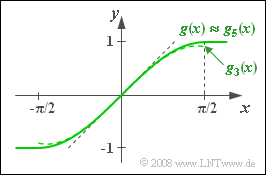
| − | Der Zusammenhang zwischen dem Eingangssignal $x(t)$ und dem Ausgangssignal $y(t)$ ist im Bereich zwischen $-\pi/2$ und $+\pi/2$ durch die folgende Kennlinie gegeben. | + | Der Zusammenhang zwischen dem Eingangssignal $x(t)$ und dem Ausgangssignal $y(t)$ ist im Bereich zwischen $-\pi/2$ und $+\pi/2$ durch die folgende Kennlinie gegeben. |
:$$g(x) = \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - | :$$g(x) = \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - | ||
\hspace{0.05cm}\text{...}$$ | \hspace{0.05cm}\text{...}$$ | ||
| − | Der zweite Teil dieser Gleichung beschreibt dabei die Reihenentwicklung der Sinusfunktion. Als Näherungen für die nichtlineare Kennlinie werden in dieser Aufgabe verwendet: | + | Der zweite Teil dieser Gleichung beschreibt dabei die Reihenentwicklung der Sinusfunktion. |
| + | |||
| + | Als Näherungen für die nichtlineare Kennlinie werden in dieser Aufgabe verwendet: | ||
:$$g_1(x) = x\hspace{0.05cm},$$ | :$$g_1(x) = x\hspace{0.05cm},$$ | ||
:$$ g_3(x) = x- x^{3}\hspace{-0.1cm}/6\hspace{0.05cm},$$ | :$$ g_3(x) = x- x^{3}\hspace{-0.1cm}/6\hspace{0.05cm},$$ | ||
:$$g_5(x) = x- x^3\hspace{-0.1cm}/{6}+x^5\hspace{-0.1cm}/{120}\hspace{0.05cm}.$$ | :$$g_5(x) = x- x^3\hspace{-0.1cm}/{6}+x^5\hspace{-0.1cm}/{120}\hspace{0.05cm}.$$ | ||
| − | Es wird stets das Eingangssignal $x(t) = A \cdot \cos(\omega_0 \cdot t)$ vorausgesetzt, wobei für die (dimensionslose) Signalamplitude die Werte $A = 0.5$, $A = 1.0$ und $A = 1.5$ zu betrachten sind. | + | Es wird stets das Eingangssignal $x(t) = A \cdot \cos(\omega_0 \cdot t)$ vorausgesetzt, wobei für die (dimensionslose) Signalamplitude die Werte $A = 0.5$, $A = 1.0$ und $A = 1.5$ zu betrachten sind. |
| + | |||
| + | |||
| + | |||
| Zeile 22: | Zeile 27: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe bezieht sich auf das Kapitel [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|Nichtlineare Verzerrungen]]. | + | *Die Aufgabe bezieht sich auf das Kapitel [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|Nichtlineare Verzerrungen]]. |
| − | *Die sich ergebenden Signalverläufe für $x(t)$ und $y(t)$ sind auf der Seite [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen#Beschreibung_nichtlinearer_Systeme|Beschreibung nichtlinearer Systeme]] grafisch dargestellt. | + | *Die sich ergebenden Signalverläufe für $x(t)$ und $y(t)$ sind auf der Seite [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen#Beschreibung_nichtlinearer_Systeme|Beschreibung nichtlinearer Systeme]] grafisch dargestellt. |
| − | *Alle hier abgefragten Leistungen beziehen sich auf den Widerstand $R = 1 \ \rm \Omega$ und haben somit die Einheit ${\rm V}^2$. | + | *Alle hier abgefragten Leistungen beziehen sich auf den Widerstand $R = 1 \ \rm \Omega$ und haben somit die Einheit ${\rm V}^2$. |
*Als bekannt vorausgesetzt werden die folgenden trigonometrischen Beziehungen: | *Als bekannt vorausgesetzt werden die folgenden trigonometrischen Beziehungen: | ||
:$$\cos^3(\alpha) = {3}/{4} \cdot \cos(\alpha) + {1}/{4} \cdot \cos(3\alpha) | :$$\cos^3(\alpha) = {3}/{4} \cdot \cos(\alpha) + {1}/{4} \cdot \cos(3\alpha) | ||
| Zeile 37: | Zeile 42: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welchen Klirrfaktor $K$ erhält man mit der Kennliniennäherung $\underline{g_1(x)}$ unabhängig von der Amplitude $A$ des Eingangssignals? | + | {Welchen Klirrfaktor $K$ erhält man mit der Kennliniennäherung $\underline{g_1(x)}$ unabhängig von der Amplitude $A$ des Eingangssignals? |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 0. } $\ \%$ | $K \ = \ $ { 0. } $\ \%$ | ||
| − | {Berechnen Sie den Klirrfaktor $K$ für das Eingangssignal $x(t) = A \cdot \cos(\omega_0 \cdot t)$ und die Näherung $\underline{g_3(x)}$. <br>Welche Werte ergeben sich für $A = 0.5$ und $A = 1.0$? | + | {Berechnen Sie den Klirrfaktor $K$ für das Eingangssignal $x(t) = A \cdot \cos(\omega_0 \cdot t)$ und die Näherung $\underline{g_3(x)}$. <br>Welche Werte ergeben sich für $A = 0.5$ und $A = 1.0$? |
|type="{}"} | |type="{}"} | ||
$A = 0.5\hspace{-0.08cm}:\ \ K \ = \ $ { 1.08 3% } $\ \%$ | $A = 0.5\hspace{-0.08cm}:\ \ K \ = \ $ { 1.08 3% } $\ \%$ | ||
| Zeile 48: | Zeile 53: | ||
| − | {Wie lautet der Klirrfaktor für $\underline{A = 1.0}$ unter Berücksichtigung der Näherung $\underline{g_5(x)}$? | + | {Wie lautet der Klirrfaktor für $\underline{A = 1.0}$ unter Berücksichtigung der Näherung $\underline{g_5(x)}$? |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 4.45 3% } $\ \%$ | $K \ = \ $ { 4.45 3% } $\ \%$ | ||
| − | {Welche der folgenden Aussagen treffen zu? Hierbei bezeichnet $K$ den Klirrfaktor der Sinusfunktion $g(x)$. <br>$K_{\rm g3}$ und $K_{\rm g5}$ | + | {Welche der folgenden Aussagen treffen zu? Hierbei bezeichnet $K$ den Klirrfaktor der Sinusfunktion $g(x)$. <br>$K_{\rm g3}$ und $K_{\rm g5}$ basieren auf den Näherungen $g_3(x)$ bzw. $g_5(x)$. |
|type="[]"} | |type="[]"} | ||
| − | + $K_{\rm g5}$ stellt im Allgemeinen eine bessere Näherung für $K$ dar als $K_{\rm g3}$. | + | + $K_{\rm g5}$ stellt im Allgemeinen eine bessere Näherung für $K$ dar als $K_{\rm g3}$. |
| − | - Für $A = 1.0$ gilt $K_{\rm g3} < K_{\rm g5}$. | + | - Für $A = 1.0$ gilt $K_{\rm g3} < K_{\rm g5}$. |
| − | + Für $A = 0.5$ wird $K_{\rm g3} \approx K_{\rm g5}$ gelten. | + | + Für $A = 0.5$ wird $K_{\rm g3} \approx K_{\rm g5}$ gelten. |
Version vom 28. Oktober 2019, 17:34 Uhr
Wie betrachten ein System mit Eingang $x(t)$ und Ausgang $y(t)$. Zur einfacheren Darstellung werden die Signale als dimensionslos betrachtet.
Der Zusammenhang zwischen dem Eingangssignal $x(t)$ und dem Ausgangssignal $y(t)$ ist im Bereich zwischen $-\pi/2$ und $+\pi/2$ durch die folgende Kennlinie gegeben.
- $$g(x) = \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \hspace{0.05cm}\text{...}$$
Der zweite Teil dieser Gleichung beschreibt dabei die Reihenentwicklung der Sinusfunktion.
Als Näherungen für die nichtlineare Kennlinie werden in dieser Aufgabe verwendet:
- $$g_1(x) = x\hspace{0.05cm},$$
- $$ g_3(x) = x- x^{3}\hspace{-0.1cm}/6\hspace{0.05cm},$$
- $$g_5(x) = x- x^3\hspace{-0.1cm}/{6}+x^5\hspace{-0.1cm}/{120}\hspace{0.05cm}.$$
Es wird stets das Eingangssignal $x(t) = A \cdot \cos(\omega_0 \cdot t)$ vorausgesetzt, wobei für die (dimensionslose) Signalamplitude die Werte $A = 0.5$, $A = 1.0$ und $A = 1.5$ zu betrachten sind.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Nichtlineare Verzerrungen.
- Die sich ergebenden Signalverläufe für $x(t)$ und $y(t)$ sind auf der Seite Beschreibung nichtlinearer Systeme grafisch dargestellt.
- Alle hier abgefragten Leistungen beziehen sich auf den Widerstand $R = 1 \ \rm \Omega$ und haben somit die Einheit ${\rm V}^2$.
- Als bekannt vorausgesetzt werden die folgenden trigonometrischen Beziehungen:
- $$\cos^3(\alpha) = {3}/{4} \cdot \cos(\alpha) + {1}/{4} \cdot \cos(3\alpha) \hspace{0.05cm}, $$
- $$ \cos^5(\alpha) = {10}/{16} \cdot \cos(\alpha) + {5}/{16} \cdot \cos(3\alpha) + {1}/{16} \cdot \cos(5\alpha)\hspace{0.05cm}.$$
Fragebogen
Musterlösung
(2) Das analytische Spektrum (nur positive Frequenzen) des Eingangssignals lautet:
- $$X_+(f) = A \cdot {\rm \delta}(f- f_0) .$$
Am Ausgang der nichtlinearen Kennlinie $g_3(x)$ liegt dann folgendes Signal an:
- $$y(t) = A \cdot {\rm cos}(\omega_0 t ) - \frac{A^3}{6} \cdot {\rm cos}^3(\omega_0 t )= A \cdot {\rm cos}(\omega_0 t ) - \frac{3}{4} \cdot \frac{A^3}{6} \cdot {\rm cos}(\omega_0 t )- \frac{1}{4} \cdot \frac{A^3}{6} \cdot {\rm cos}(3\omega_0 t ) = A_1 \cdot {\rm cos}(\omega_0 t ) + A_3 \cdot {\rm cos}(3\omega_0 t ).$$
Für die Koeffizienten $A_1$ und $A_3$ erhält man durch Koeffizientenvergleich:
- $$A_1 = A - {A^3}\hspace{-0.1cm}/{8}, \hspace{0.5cm}A_3 = - {A^3}\hspace{-0.1cm}/{24}.$$
Mit $A = 0.5$ ergibt sich $A_1 \approx 0.484$ und $A_3 \approx 0.005$. Somit lautet der Klirrfaktor:
- $$K = K_3 ={|A_3|}/{A_1}= {0.005}/{0.484} \hspace{0.15cm}\underline{ = 1.08\%}.$$
Anzumerken ist, dass bei der Näherung $g_3(x)$ nur der kubische Anteil $K_3$ des Klirrfaktors wirksam ist.
Für $A = 1.0$ und $A = 1.5$ ergeben sich folgende Zahlenwerte:
- $$A = 1.0: A_1 \approx 0.875, \hspace{0.2cm} A_3 \approx -0.041\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{K \approx 4.76\%}\; \; \Rightarrow \; \; K_{g3},$$
- $$A = 1.5: A_1 \approx 1.078, \hspace{0.2cm} A_3 \approx -0.140\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \hspace{0.15cm}{K \approx 13 \%}.$$
(3) In ähnlicher Weise wie beim Unterpunkt (2) gilt nun
- $$y(t) = A_1 \cdot {\rm cos}(\omega_0 t ) + A_3 \cdot {\rm cos}(3\omega_0 t )+ A_5 \cdot {\rm cos}(5\omega_0 t )$$
mit folgenden Koeffizienten:
- $$A_1 = A - {A^3}\hspace{-0.1cm}/{8} + {A^5}\hspace{-0.1cm}/{192},\hspace{0.3cm} A_3 = - {A^3}\hspace{-0.1cm}/{24} + {A^5}\hspace{-0.1cm}/{384},\hspace{0.3cm} A_5 = {A^5}\hspace{-0.1cm}/{1920}.$$
Daraus ergeben sich mit $A=1$ die Zahlenwerte:
- $$A_1 \approx 1 -0.125 +0.005 = 0.880,\hspace{0.3cm} A_3 \approx -0.042 +0.003 = -0.039,\hspace{0.3cm} A_5 \approx 0.0005$$
- $$\Rightarrow \hspace{0.3cm}K_3 = {|A_3|}/{A_1}= 0.0443,\hspace{0.3cm}K_5 = {|A_5|}/{A_1}= 0.0006 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K = \sqrt{K_3^2 + K_5^2} \hspace{0.15cm}\underline{\approx 4.45\%} \; \; \Rightarrow \; \; K_{g5}.$$
(4) Richtig sind die Lösungsvorschläge 1 und 3:
- Der Ansatz $g_5(x)$ ist im gesamten Bereich eine bessere Näherung für die Sinusfunktion $g(x)$ als die Näherung $g_3(x)$.
- Deshalb ist der in der Teilaufgabe (3) berechnete Wert $K_{g5}$ eine bessere Näherung für den tatsächlichen Klirrfaktor als $K_{g3}$.
die erste Aussage ist somit richtig. - Die zweite Aussage ist falsch, wie schon die Berechnung für $A=1$ gezeigt hat: $K_{g3} \approx 4.76 \%$ ist größer als $K_{g5} \approx 4.45 \%$.
- Der Grund hierfür ist, dass $g_3(x)$ unterhalb von $g_5(x)$ liegt und damit auch eine größere Abweichung vom linearen Verlauf vorliegt.
- Für $A=0.5$ wird $K_{g5} \approx K_{g3} = 1.08 \%$ gelten.
- Schon die Kennlinie auf der Angabenseite zeigt, dass für $|x| \le 0.5$ die beiden Funktionen $g_3(x)$ und $g_5(x)$ innerhalb der Zeichengenauigkeit nicht zu unterscheiden sind.
- Damit ergeben sich auch gleiche Klirrfaktoren.