Stochastische Signaltheorie/Erzeugung von diskreten Zufallsgrößen: Unterschied zwischen den Versionen
| Zeile 27: | Zeile 27: | ||
==Realisierung von PN-Generatoren== | ==Realisierung von PN-Generatoren== | ||
<br> | <br> | ||
| − | Pseudozufallsgeneratoren werden meist durch rückgekoppelte Schieberegister realisiert, wobei zu jedem Taktzeitpunkt der Inhalt des Registers um eine Stelle nach rechts geschoben wird (siehe Grafik). Für das aktuell erzeugte Symbol gilt mit $g_l ∈ \{0, 1\}$ und $l = 1$, ... , $L–1$: | + | Pseudozufallsgeneratoren werden meist durch rückgekoppelte Schieberegister realisiert, wobei zu jedem Taktzeitpunkt der Inhalt des Registers um eine Stelle nach rechts geschoben wird (siehe Grafik). Für das aktuell erzeugte Symbol gilt mit $g_l ∈ \{0, 1\}$ und $l = 1$, ... , $L–1$: |
:$$z_\nu = (g_1\cdot z_{\nu-1}+g_2\cdot z_{\nu-2}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_l\cdot z_{\nu-l}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_{L-1}\cdot z_{\nu-L+1}+ z_{\nu-L})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$ | :$$z_\nu = (g_1\cdot z_{\nu-1}+g_2\cdot z_{\nu-2}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_l\cdot z_{\nu-l}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_{L-1}\cdot z_{\nu-L+1}+ z_{\nu-L})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$ | ||
| − | *Die zu vorherigen Zeitpunkten generierten Binärwerte $z_{ν-1}$ bis $z_{ν-L}$ sind in den Speicherzellen des Schieberegisters abgelegt. | + | *Die zu vorherigen Zeitpunkten generierten Binärwerte $z_{ν-1}$ bis $z_{ν-L}$ sind in den Speicherzellen des Schieberegisters abgelegt. |
| − | *Die Koeffizienten $g_1$, ... , $g_{L–1}$ sind ebenfalls Binärwerte, wobei eine $1$ eine Rückkopplung an der entsprechenden Stelle kennzeichnet und eine $0$ keine Rückführung. | + | *Die Koeffizienten $g_1$, ... , $g_{L–1}$ sind ebenfalls Binärwerte, wobei eine $1$ eine Rückkopplung an der entsprechenden Stelle kennzeichnet und eine $0$ keine Rückführung. |
*Die Modulo-2-Addition kann zum Beispiel durch eine XOR-Verknüpfung realisiert werden: | *Die Modulo-2-Addition kann zum Beispiel durch eine XOR-Verknüpfung realisiert werden: | ||
[[Datei:P_ID34__Sto_T_2_5_S2_neu.png |right|frame| Pseudo-Noise-Generator]] | [[Datei:P_ID34__Sto_T_2_5_S2_neu.png |right|frame| Pseudo-Noise-Generator]] | ||
:$$(x + y)\hspace{0.1cm} \rm mod\hspace{0.1cm}2 = \it x\hspace{0.1cm}\rm XOR\hspace{0.1cm} \it y = \left\{\begin{array}{*{2}{c}} \rm 0 & \rm falls\hspace{0.1cm} \it x= y,\\ 1 & \rm falls\hspace{0.1cm} \it x\neq y. \\ \end{array} \right.$$ | :$$(x + y)\hspace{0.1cm} \rm mod\hspace{0.1cm}2 = \it x\hspace{0.1cm}\rm XOR\hspace{0.1cm} \it y = \left\{\begin{array}{*{2}{c}} \rm 0 & \rm falls\hspace{0.1cm} \it x= y,\\ 1 & \rm falls\hspace{0.1cm} \it x\neq y. \\ \end{array} \right.$$ | ||
| − | Die statistischen Eigenschaften der erzeugten Pseudonoise-Zufallsfolge $〈z_{\rm ν}〉$ werden im Wesentlichen bestimmt durch | + | Die statistischen Eigenschaften der erzeugten Pseudonoise-Zufallsfolge $〈z_{\rm ν}〉$ werden im Wesentlichen bestimmt durch |
| − | *den '''Grad''' $L$, und | + | *den '''Grad''' $L$, und |
| − | *die '''Rückführungskoeffizienten''' $g_{\hspace{0.05cm}l}$ (mit $l = 1$, ... , $L-1$ | + | *die '''Rückführungskoeffizienten''' $g_{\hspace{0.05cm}l}$ $($mit $l = 1$, ... , $L-1)$. |
| − | Voraussetzung für die Entstehung einer PN-Folge ist, dass nicht alle Speicherelemente mit Nullen vorbelegt sind, da sonst die Modulo-2-Addition immer nur das Symbol $0$ erzeugen würde. | + | Voraussetzung für die Entstehung einer PN-Folge ist, dass nicht alle Speicherelemente mit Nullen vorbelegt sind, da sonst die Modulo-2-Addition immer nur das Symbol $0$ erzeugen würde. |
Zur Kennzeichnung unterschiedlicher PN-Generatoren verwendet man in der Literatur alternativ: | Zur Kennzeichnung unterschiedlicher PN-Generatoren verwendet man in der Literatur alternativ: | ||
| − | *die sogenannten '''Generatorpolynome''' von der Art | + | *die sogenannten '''Generatorpolynome''' von der Art |
:$$G(D) = g_L\cdot D^L+g_{L-1}\cdot D^{L-1}+ \ \text{...} \ +g_1\cdot D+g_0 .$$ | :$$G(D) = g_L\cdot D^L+g_{L-1}\cdot D^{L-1}+ \ \text{...} \ +g_1\cdot D+g_0 .$$ | ||
| − | :Hierbei ist stets $g_0 = g_L = 1$ zu setzen und $D$ ein formaler Parameter, der eine Verzögerung um einen Takt angibt ( | + | :Hierbei ist stets $g_0 = g_L = 1$ zu setzen und $D$ ein formaler Parameter, der eine Verzögerung um einen Takt angibt $(D^L$ kennzeichnet eine Verzögerung um $L$ Takte$)$; |
| − | *die '''Oktaldarstellung''' der Binärzahl $(g_L\ \text{ ...} \ g_2 \ g_1 \ g_0). | + | *die '''Oktaldarstellung''' der Binärzahl $(g_L\ \text{ ...} \ g_2 \ g_1 \ g_0)$. Wichtig ist, dass hierbei die Rückkopplungskoeffizienten – von rechts mit $g_0$ beginnend – zu Tripeln zusammengefasst und diese oktal $(0 \ \text{...}\ 7)$ geschrieben werden. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 2:}$ | $\text{Beispiel 2:}$ | ||
| − | Das Generatorpolynom $D^4 + D^3 + 1$ gehört zu einem Schieberegister vom Grad $L = 4$ mit folgender Oktaldarstellung | + | Das Generatorpolynom $D^4 + D^3 + 1$ gehört zu einem Schieberegister vom Grad $L = 4$ mit folgender Oktaldarstellung |
:$$(g_4 \ g_3 \ g_2 \ g_1 \ g_0) = (11001)_{\rm bin} = (31)_{\rm oct}. $$}} | :$$(g_4 \ g_3 \ g_2 \ g_1 \ g_0) = (11001)_{\rm bin} = (31)_{\rm oct}. $$}} | ||
==Folgen maximaler Länge (M-Sequenzen)== | ==Folgen maximaler Länge (M-Sequenzen)== | ||
<br> | <br> | ||
| − | Sind nicht alle $L$ Speicherzellen des Schieberegisters mit Nullen vorbelegt, so entsteht stets eine periodische Zufallsfolge $〈z_ν\rangle$: | + | Sind nicht alle $L$ Speicherzellen des Schieberegisters mit Nullen vorbelegt, so entsteht stets eine periodische Zufallsfolge $〈z_ν\rangle$: |
| − | *Die Periodenlänge $P$ dieser Folge hängt im starken Maße von den Rückkopplungskoeffizienten ab. | + | *Die Periodenlänge $P$ dieser Folge hängt im starken Maße von den Rückkopplungskoeffizienten ab. |
| − | *Für jeden Grad $L$ gibt es zumindest eine Konfiguration mit der ''maximalen Periodenlänge'' | + | *Für jeden Grad $L$ gibt es zumindest eine Konfiguration mit der ''maximalen Periodenlänge'' |
:$$P_{\rm max} = \rm 2^{\it L}-\rm 1.$$ | :$$P_{\rm max} = \rm 2^{\it L}-\rm 1.$$ | ||
| − | Eine solche PN-Folge bezeichnet man auch oft als $\rm M-Sequenz$, wobei das $\rm M$ für „Maximal“ steht. | + | Eine solche PN-Folge bezeichnet man auch oft als $\rm M-Sequenz$, wobei das $\rm M$ für „Maximal“ steht. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Vorerst ohne Beweis:}$ Eine M-Sequenz kann man daran erkennen, dass das Generatorpolynom $G(D)$ primitiv ist. Wie im Buch [[Kanalcodierung]] | + | $\text{Vorerst ohne Beweis:}$ |
| + | # Eine $\rm M-Sequenz$ kann man daran erkennen, dass das Generatorpolynom $G(D)$ primitiv ist. | ||
| + | # Wie im Buch [[Kanalcodierung]] ausführlich dargelegt wird, bezeichnet man ein Polynom $G(D)$ vom Grad $L$ als '''primitiv''', wenn folgende Bedingung erfüllt ist: | ||
:$$\frac{(D^n+\rm 1)}{\it G(D)} \neq 0\hspace{0.5cm} {\rm f\ddot{u}r}\hspace{0.5cm}\it n<P_{\rm max} \rm = \rm 2^{\it L}-\rm 1.$$}} | :$$\frac{(D^n+\rm 1)}{\it G(D)} \neq 0\hspace{0.5cm} {\rm f\ddot{u}r}\hspace{0.5cm}\it n<P_{\rm max} \rm = \rm 2^{\it L}-\rm 1.$$}} | ||
[[Datei: P_ID35__Sto_T_2_5_S5.png|right|frame|Zusammenstellung einiger günstiger Generatorpolynome]] | [[Datei: P_ID35__Sto_T_2_5_S5.png|right|frame|Zusammenstellung einiger günstiger Generatorpolynome]] | ||
| − | In der Tabelle sind | + | <br><br><br><br> |
| + | In der Tabelle sind PN-Generatoren maximaler Länge bis zum Grad $L = 31$ aufgeführt. | ||
*Die Auswahl ist auf Konfigurationen mit nur einer Anzapfung – also mit zwei Rückführungen – beschränkt. | *Die Auswahl ist auf Konfigurationen mit nur einer Anzapfung – also mit zwei Rückführungen – beschränkt. | ||
| − | *Das bedeutet, dass die zugehörigen Polynome | + | *Das bedeutet, dass die zugehörigen Polynome nur aus drei Summanden bestehen. |
*Für Applikationen, die eine hohe Geschwindigkeit erfordern, sind solche Generatoren sehr nützlich. | *Für Applikationen, die eine hohe Geschwindigkeit erfordern, sind solche Generatoren sehr nützlich. | ||
<br clear=all> | <br clear=all> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 3:}$ Ein Schieberegister vom Grad $L = 4$ mit Oktalkennung $(31)$ und Generatorpolynom $G(D) = D^4 + D^3 + 1$ führt zu einer Folge maximaler Länge: | + | $\text{Beispiel 3:}$ Ein Schieberegister vom Grad $L = 4$ mit Oktalkennung $(31)$ und Generatorpolynom $G(D) = D^4 + D^3 + 1$ führt zu einer Folge maximaler Länge: |
:$$P_{\rm max} = 2^4 - 1 = 15.$$ | :$$P_{\rm max} = 2^4 - 1 = 15.$$ | ||
Der mathematische Nachweis hierfür ist aufwändig: | Der mathematische Nachweis hierfür ist aufwändig: | ||
| − | *Man muss anhand obiger Polynomdivision für $n = 1$, ... , $14$ zeigen, dass der Quotient stets ungleich | + | *Man muss anhand obiger Polynomdivision für $n = 1$, ... , $14$ zeigen, dass der Quotient stets ungleich Null ist. |
| − | *Erst die Division $(D^{15} + 1)/G(D)$ darf ein Ergebnis ohne Rest liefern. | + | *Erst die Division $(D^{15} + 1)/G(D)$ darf ein Ergebnis ohne Rest liefern. |
| − | *Hierbei ist zu berücksichtigen, dass in der Modulo-2-Algebra $+1$ und $–1$ identisch sind. }} | + | *Hierbei ist zu berücksichtigen, dass in der Modulo-2-Algebra $+1$ und $–1$ identisch sind. }} |
| − | |||
| − | |||
| Zeile 90: | Zeile 91: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Das zum Generatorpolynom $G(D)$ gehörige '''reziproke Polynom''' lautet: | + | Das zum Generatorpolynom $G(D)$ gehörige '''reziproke Polynom''' lautet: |
:$$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$}} | :$$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$}} | ||
| − | Zwischen den beiden Schiebregistern mit den Polynomen $G(D)$ bzw. $G_{\rm R}(D)$ bestehen folgende Zusammenhänge: | + | Zwischen den beiden Schiebregistern mit den Polynomen $G(D)$ bzw. $G_{\rm R}(D)$ bestehen folgende Zusammenhänge: |
| − | *Liefert $G(D)$ eine Folge maximaler Länge ⇒ $P_{\rm max} = 2^L - 1$, so ist auch die Periodenlänge des reziproken Polynoms $G_{\rm R}(D)$ maximal. | + | *Liefert $G(D)$ eine Folge maximaler Länge ⇒ $P_{\rm max} = 2^L - 1$, so ist auch die Periodenlänge des reziproken Polynoms $G_{\rm R}(D)$ maximal. |
| − | *Die Ausgangsfolgen reziproker Konfigurationen sind zueinander invers: | + | *Die Ausgangsfolgen reziproker Konfigurationen sind zueinander invers. Das heißt: |
| − | *Die Folge von $G(D)$ – von rechts nach links gelesen – ergibt die Folge der reziproken Anordnung $G_{\rm R}(D)$. | + | *Die Folge von $G(D)$ – von rechts nach links gelesen – ergibt die Folge der reziproken Anordnung $G_{\rm R}(D)$. |
| − | In [[Stochastische_Signaltheorie/Erzeugung_von_diskreten_Zufallsgrößen#Folgen_maximaler_L.C3.A4nge_.28M-Sequenzen.29|obiger Tabelle]] sind in der dritten Spalte die zu $G(D)$ zugehörigen reziproken Polynome $G_{\rm R}(D)$ bis zum Registergrad $L = 31$ angegeben. | + | In [[Stochastische_Signaltheorie/Erzeugung_von_diskreten_Zufallsgrößen#Folgen_maximaler_L.C3.A4nge_.28M-Sequenzen.29|obiger Tabelle]] sind in der dritten Spalte die zu $G(D)$ zugehörigen reziproken Polynome $G_{\rm R}(D)$ bis zum Registergrad $L = 31$ angegeben. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 4:}$ | $\text{Beispiel 4:}$ | ||
| − | Wir betrachten wieder den Grad $L = 4$. | + | Wir betrachten wieder den Grad $L = 4$. |
| − | *Ausgehend von der Schieberegisterstruktur $(31)_{\rm oct}$ erhält man für das reziproke Polynom | + | *Ausgehend von der Schieberegisterstruktur $(31)_{\rm oct}$ erhält man für das reziproke Polynom |
:$$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} + D^{ -4})=D^{ 4}+D^{1}+\rm 1$$ | :$$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} + D^{ -4})=D^{ 4}+D^{1}+\rm 1$$ | ||
| − | :und damit die Konfiguration mit der Oktalkennung $(23)$. | + | :und damit die Konfiguration mit der Oktalkennung $(23)$. |
| − | *Die entsprechenden Ausgangsfolgen haben jeweils die maximale Periodenlänge $P_{\rm max} = 15$ und sind zueinander invers: | + | *Die entsprechenden Ausgangsfolgen haben jeweils die maximale Periodenlänge $P_{\rm max} = 15$ und sind zueinander invers: |
| − | + | ** ... $0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1$ ... | |
| − | + | ** ... $0 \ 1 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1$ ... | |
| − | *Das bedeutet, dass die obere Ausgangsfolge von $(31)$, von rechts nach links gelesen, die unten angegebene Folge der reziproken Anordnung $(23)$ ergibt. | + | *Das bedeutet, dass die obere Ausgangsfolge von $(31)$, von rechts nach links gelesen, die unten angegebene Folge der reziproken Anordnung $(23)$ ergibt. |
*Zu erkennen ist allerdings eine zyklische Phasenverschiebung um vier Binärstellen. }} | *Zu erkennen ist allerdings eine zyklische Phasenverschiebung um vier Binärstellen. }} | ||
| − | Die in diesem Abschnitt behandelte Thematik ist im Lernvideo [[Erläuterung_der_PN–Generatoren_an_einem_Beispiel_(Lernvideo)|Erläuterung der PN-Generatoren an einem Beispiel]] zusammengefasst. | + | Die in diesem Abschnitt behandelte Thematik ist im Lernvideo [[Erläuterung_der_PN–Generatoren_an_einem_Beispiel_(Lernvideo)|Erläuterung der PN-Generatoren an einem Beispiel]] zusammengefasst. |
==Erzeugung mehrstufiger Zufallsgrößen== | ==Erzeugung mehrstufiger Zufallsgrößen== | ||
<br> | <br> | ||
| − | Viele höhere Programmiersprachen bieten Pseudo-Zufallsgeneratoren an, die reelle, zwischen $0$ und $1$ gleichverteilte Zufallszahlen $x$ liefern. Beispielsweise lautet ein entsprechender C-Funktionsaufruf: | + | Viele höhere Programmiersprachen bieten Pseudo-Zufallsgeneratoren an, die reelle, zwischen $0$ und $1$ gleichverteilte Zufallszahlen $x$ liefern. Beispielsweise lautet ein entsprechender C-Funktionsaufruf: |
:$$x = \text{random()}.$$ | :$$x = \text{random()}.$$ | ||
| − | Durch sukzessives Aufrufen der „Random-Funktion” entsteht eine periodisch sich wiederholende Folge reeller Zahlen, wobei alle Funktionswerte $0 \le x < 1$ gleichwahrscheinlich sind ⇒ siehe Kapitel [[Stochastische_Signaltheorie/Gleichverteilte_Zufallsgrößen|Gleichverteilte Zufallsgrößen]]. | + | Durch sukzessives Aufrufen der „Random-Funktion” entsteht eine periodisch sich wiederholende Folge reeller Zahlen, wobei alle Funktionswerte $0 \le x < 1$ gleichwahrscheinlich sind ⇒ siehe Kapitel [[Stochastische_Signaltheorie/Gleichverteilte_Zufallsgrößen|Gleichverteilte Zufallsgrößen]]. |
| − | * Da die Periodendauer $P$ jedoch sehr groß ist, kann diese Folge als ''pseudozufällig'' angesehen werden. | + | * Da die Periodendauer $P$ jedoch sehr groß ist, kann diese Folge als ''pseudozufällig'' angesehen werden. |
*Durch Angabe eines Startwertes wird an bestimmten Stellen der Pseudozufallsfolge begonnen. | *Durch Angabe eines Startwertes wird an bestimmten Stellen der Pseudozufallsfolge begonnen. | ||
| − | Bei der Generierung einer wertdiskreten mehrstufigen Zufallsgröße $z$ wird zweckmäßigerweise von einer solchen | + | Bei der Generierung einer wertdiskreten mehrstufigen Zufallsgröße $z$ wird zweckmäßigerweise von einer solchen gleichverteilten Zufallsgröße $x$ ausgegangen. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 5:}$ | $\text{Beispiel 5:}$ | ||
| − | Die | + | Die Grafik zeigt das Prinzip für den Sonderfall $M = 3$, wobei die gewünschten Auftrittswahrscheinlichkeiten mit $p_0$, $p_1$ und $p_2$ bezeichnet sind. |
[[Datei:P_ID457__Sto_T_2_5_S6neu.png|right|frame|Zur Erzeugung mehrstufiger Zufallsgrößen]] | [[Datei:P_ID457__Sto_T_2_5_S6neu.png|right|frame|Zur Erzeugung mehrstufiger Zufallsgrößen]] | ||
Dann gilt: | Dann gilt: | ||
| − | *Ist der aktuelle Wert $x$ der zwischen $0$ und $1$ gleichverteilten Zufallsgröße kleiner als $p_0$, so wird die ternäre Zufallsgröße $z =$ | + | *Ist der aktuelle Wert $x$ der zwischen $0$ und $1$ gleichverteilten Zufallsgröße kleiner als $p_0$, so wird die ternäre Zufallsgröße $z = 0$ gesetzt. |
| − | *Im Bereich $p_0 ≤ x < p_0 + p_1$ wird $z = 1$ | + | *Im Bereich $p_0 ≤ x < p_0 + p_1$ wird $z = 1$ ausgegeben. |
| − | *Für $x \ge p_0 + p_1$ wird die Zufallsgröße zu $z =2$. | + | *Für $x \ge p_0 + p_1$ wird die Zufallsgröße zu $z =2$. |
<br clear=all> | <br clear=all> | ||
| − | Im aufgeführten C-Programm ergibt sich für $M = 3$ und für den aktuellen Zufallswert $x = 0.57$ für das Produkt $x · M = 0.57 · 3 = 1.71$ und somit die diskrete Zufallsgröße $z = 1$. Für einen zweiten Zufallswert $x = 0.95$ würde die Funktion dagegen das Ergebnis $z = 2$ liefern. | + | Im aufgeführten C-Programm ergibt sich für $M = 3$ und für den aktuellen Zufallswert $x = 0.57$ für das Produkt $x · M = 0.57 · 3 = 1.71$ und somit die diskrete Zufallsgröße $z = 1$. Für einen zweiten Zufallswert $x = 0.95$ würde die Funktion dagegen das Ergebnis $z = 2$ liefern. |
| − | Aus | + | Aus Verständnisgründen wurde hier eine umständliche Programmierung gewählt. Der angegebene C-Programmteil könnte auch kompakter geschrieben werden: |
:$$\text{\{ float random(); return((long) (random()*M)); \} }$$}} | :$$\text{\{ float random(); return((long) (random()*M)); \} }$$}} | ||
Version vom 13. November 2019, 18:42 Uhr
Inhaltsverzeichnis
Pseudozufallsgrößen
Eine Möglichkeit zur Erzeugung einer binären Zufallsfolge $〈z_{\rm ν}〉 ∈ \{0, 1\}$ mit guten statistischen Eigenschaften bieten die so genannten Pseudozufallsgeneratoren, auch bekannt unter dem Namen PN-Generatoren, wobei „PN” für Pseudonoise steht.
Diese besitzen folgende Eigenschaften:
- Die durch einen solchen Generator erzeugte Binärfolge ist im strengen Sinne nicht stochastisch, sondern weist periodische und damit deterministische Eigenschaften auf.
- Ist die Periodenlänge $P$ hinreichend groß, erscheint die Folge für einen Betrachter als zufällig mit für viele Anwendungen hinreichend guten statistischen Eigenschaften.
- Vorteil eines Pseudozufallsgenerators gegenüber einer „echten” stochastischen Quelle ist, dass die Zufallsfolge bei Kenntnis einiger weniger Parameter reproduzierbar ist.
$\text{Beispiel 1:}$ Aus der zuletzt genannten Eigenschaft heraus ergeben sich auch die wichtigsten Anwendungen der Pseudonoise-Generatoren:
- zum einen die Fehlerhäufigkeitsmessung bei der Digitalsignalübertragung,
- zum zweiten zur Bandspreizung bei CDMA (Code Division Multiple Access).
Bei einem solchen Spread Spectrum System wird das Sendesignal mit einer binären Zufallsfolge moduliert, deren Symbolfolgefrequenz deutlich größer als die Bitfrequenz ist. Dadurch bietet sich die Möglichkeit der Mehrfachausnutzung von Kanälen. Da am Empfänger die gleiche Folge phasenrichtig zugesetzt werden muss, ist auch hier der Einsatz von reproduzierbaren PN-Sequenzen üblich.
Ausführliche Informationen zu den Bandspreizverfahren finden Sie im Kapitel UMTS – Universal Mobile Telecommunications System des Buches „Beispiele von Nachrichtensystemen” .
Realisierung von PN-Generatoren
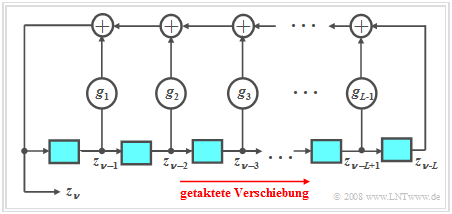
Pseudozufallsgeneratoren werden meist durch rückgekoppelte Schieberegister realisiert, wobei zu jedem Taktzeitpunkt der Inhalt des Registers um eine Stelle nach rechts geschoben wird (siehe Grafik). Für das aktuell erzeugte Symbol gilt mit $g_l ∈ \{0, 1\}$ und $l = 1$, ... , $L–1$:
- $$z_\nu = (g_1\cdot z_{\nu-1}+g_2\cdot z_{\nu-2}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_l\cdot z_{\nu-l}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_{L-1}\cdot z_{\nu-L+1}+ z_{\nu-L})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$
- Die zu vorherigen Zeitpunkten generierten Binärwerte $z_{ν-1}$ bis $z_{ν-L}$ sind in den Speicherzellen des Schieberegisters abgelegt.
- Die Koeffizienten $g_1$, ... , $g_{L–1}$ sind ebenfalls Binärwerte, wobei eine $1$ eine Rückkopplung an der entsprechenden Stelle kennzeichnet und eine $0$ keine Rückführung.
- Die Modulo-2-Addition kann zum Beispiel durch eine XOR-Verknüpfung realisiert werden:
- $$(x + y)\hspace{0.1cm} \rm mod\hspace{0.1cm}2 = \it x\hspace{0.1cm}\rm XOR\hspace{0.1cm} \it y = \left\{\begin{array}{*{2}{c}} \rm 0 & \rm falls\hspace{0.1cm} \it x= y,\\ 1 & \rm falls\hspace{0.1cm} \it x\neq y. \\ \end{array} \right.$$
Die statistischen Eigenschaften der erzeugten Pseudonoise-Zufallsfolge $〈z_{\rm ν}〉$ werden im Wesentlichen bestimmt durch
- den Grad $L$, und
- die Rückführungskoeffizienten $g_{\hspace{0.05cm}l}$ $($mit $l = 1$, ... , $L-1)$.
Voraussetzung für die Entstehung einer PN-Folge ist, dass nicht alle Speicherelemente mit Nullen vorbelegt sind, da sonst die Modulo-2-Addition immer nur das Symbol $0$ erzeugen würde.
Zur Kennzeichnung unterschiedlicher PN-Generatoren verwendet man in der Literatur alternativ:
- die sogenannten Generatorpolynome von der Art
- $$G(D) = g_L\cdot D^L+g_{L-1}\cdot D^{L-1}+ \ \text{...} \ +g_1\cdot D+g_0 .$$
- Hierbei ist stets $g_0 = g_L = 1$ zu setzen und $D$ ein formaler Parameter, der eine Verzögerung um einen Takt angibt $(D^L$ kennzeichnet eine Verzögerung um $L$ Takte$)$;
- die Oktaldarstellung der Binärzahl $(g_L\ \text{ ...} \ g_2 \ g_1 \ g_0)$. Wichtig ist, dass hierbei die Rückkopplungskoeffizienten – von rechts mit $g_0$ beginnend – zu Tripeln zusammengefasst und diese oktal $(0 \ \text{...}\ 7)$ geschrieben werden.
$\text{Beispiel 2:}$ Das Generatorpolynom $D^4 + D^3 + 1$ gehört zu einem Schieberegister vom Grad $L = 4$ mit folgender Oktaldarstellung
- $$(g_4 \ g_3 \ g_2 \ g_1 \ g_0) = (11001)_{\rm bin} = (31)_{\rm oct}. $$
Folgen maximaler Länge (M-Sequenzen)
Sind nicht alle $L$ Speicherzellen des Schieberegisters mit Nullen vorbelegt, so entsteht stets eine periodische Zufallsfolge $〈z_ν\rangle$:
- Die Periodenlänge $P$ dieser Folge hängt im starken Maße von den Rückkopplungskoeffizienten ab.
- Für jeden Grad $L$ gibt es zumindest eine Konfiguration mit der maximalen Periodenlänge
- $$P_{\rm max} = \rm 2^{\it L}-\rm 1.$$
Eine solche PN-Folge bezeichnet man auch oft als $\rm M-Sequenz$, wobei das $\rm M$ für „Maximal“ steht.
$\text{Vorerst ohne Beweis:}$
- Eine $\rm M-Sequenz$ kann man daran erkennen, dass das Generatorpolynom $G(D)$ primitiv ist.
- Wie im Buch Kanalcodierung ausführlich dargelegt wird, bezeichnet man ein Polynom $G(D)$ vom Grad $L$ als primitiv, wenn folgende Bedingung erfüllt ist:
- $$\frac{(D^n+\rm 1)}{\it G(D)} \neq 0\hspace{0.5cm} {\rm f\ddot{u}r}\hspace{0.5cm}\it n<P_{\rm max} \rm = \rm 2^{\it L}-\rm 1.$$
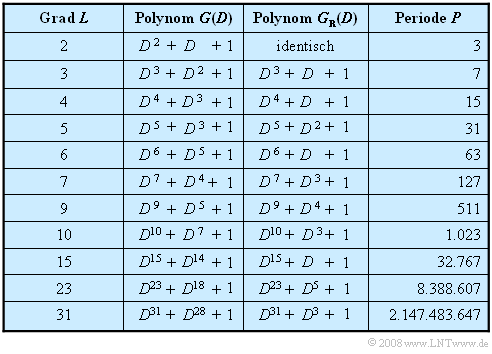
In der Tabelle sind PN-Generatoren maximaler Länge bis zum Grad $L = 31$ aufgeführt.
- Die Auswahl ist auf Konfigurationen mit nur einer Anzapfung – also mit zwei Rückführungen – beschränkt.
- Das bedeutet, dass die zugehörigen Polynome nur aus drei Summanden bestehen.
- Für Applikationen, die eine hohe Geschwindigkeit erfordern, sind solche Generatoren sehr nützlich.
$\text{Beispiel 3:}$ Ein Schieberegister vom Grad $L = 4$ mit Oktalkennung $(31)$ und Generatorpolynom $G(D) = D^4 + D^3 + 1$ führt zu einer Folge maximaler Länge:
- $$P_{\rm max} = 2^4 - 1 = 15.$$
Der mathematische Nachweis hierfür ist aufwändig:
- Man muss anhand obiger Polynomdivision für $n = 1$, ... , $14$ zeigen, dass der Quotient stets ungleich Null ist.
- Erst die Division $(D^{15} + 1)/G(D)$ darf ein Ergebnis ohne Rest liefern.
- Hierbei ist zu berücksichtigen, dass in der Modulo-2-Algebra $+1$ und $–1$ identisch sind.
Reziproke Polynome
$\text{Definition:}$ Das zum Generatorpolynom $G(D)$ gehörige reziproke Polynom lautet:
- $$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$
Zwischen den beiden Schiebregistern mit den Polynomen $G(D)$ bzw. $G_{\rm R}(D)$ bestehen folgende Zusammenhänge:
- Liefert $G(D)$ eine Folge maximaler Länge ⇒ $P_{\rm max} = 2^L - 1$, so ist auch die Periodenlänge des reziproken Polynoms $G_{\rm R}(D)$ maximal.
- Die Ausgangsfolgen reziproker Konfigurationen sind zueinander invers. Das heißt:
- Die Folge von $G(D)$ – von rechts nach links gelesen – ergibt die Folge der reziproken Anordnung $G_{\rm R}(D)$.
In obiger Tabelle sind in der dritten Spalte die zu $G(D)$ zugehörigen reziproken Polynome $G_{\rm R}(D)$ bis zum Registergrad $L = 31$ angegeben.
$\text{Beispiel 4:}$ Wir betrachten wieder den Grad $L = 4$.
- Ausgehend von der Schieberegisterstruktur $(31)_{\rm oct}$ erhält man für das reziproke Polynom
- $$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} + D^{ -4})=D^{ 4}+D^{1}+\rm 1$$
- und damit die Konfiguration mit der Oktalkennung $(23)$.
- Die entsprechenden Ausgangsfolgen haben jeweils die maximale Periodenlänge $P_{\rm max} = 15$ und sind zueinander invers:
- ... $0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1$ ...
- ... $0 \ 1 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1$ ...
- Das bedeutet, dass die obere Ausgangsfolge von $(31)$, von rechts nach links gelesen, die unten angegebene Folge der reziproken Anordnung $(23)$ ergibt.
- Zu erkennen ist allerdings eine zyklische Phasenverschiebung um vier Binärstellen.
Die in diesem Abschnitt behandelte Thematik ist im Lernvideo Erläuterung der PN-Generatoren an einem Beispiel zusammengefasst.
Erzeugung mehrstufiger Zufallsgrößen
Viele höhere Programmiersprachen bieten Pseudo-Zufallsgeneratoren an, die reelle, zwischen $0$ und $1$ gleichverteilte Zufallszahlen $x$ liefern. Beispielsweise lautet ein entsprechender C-Funktionsaufruf:
- $$x = \text{random()}.$$
Durch sukzessives Aufrufen der „Random-Funktion” entsteht eine periodisch sich wiederholende Folge reeller Zahlen, wobei alle Funktionswerte $0 \le x < 1$ gleichwahrscheinlich sind ⇒ siehe Kapitel Gleichverteilte Zufallsgrößen.
- Da die Periodendauer $P$ jedoch sehr groß ist, kann diese Folge als pseudozufällig angesehen werden.
- Durch Angabe eines Startwertes wird an bestimmten Stellen der Pseudozufallsfolge begonnen.
Bei der Generierung einer wertdiskreten mehrstufigen Zufallsgröße $z$ wird zweckmäßigerweise von einer solchen gleichverteilten Zufallsgröße $x$ ausgegangen.
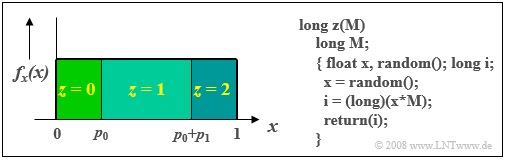
$\text{Beispiel 5:}$ Die Grafik zeigt das Prinzip für den Sonderfall $M = 3$, wobei die gewünschten Auftrittswahrscheinlichkeiten mit $p_0$, $p_1$ und $p_2$ bezeichnet sind.
Dann gilt:
- Ist der aktuelle Wert $x$ der zwischen $0$ und $1$ gleichverteilten Zufallsgröße kleiner als $p_0$, so wird die ternäre Zufallsgröße $z = 0$ gesetzt.
- Im Bereich $p_0 ≤ x < p_0 + p_1$ wird $z = 1$ ausgegeben.
- Für $x \ge p_0 + p_1$ wird die Zufallsgröße zu $z =2$.
Im aufgeführten C-Programm ergibt sich für $M = 3$ und für den aktuellen Zufallswert $x = 0.57$ für das Produkt $x · M = 0.57 · 3 = 1.71$ und somit die diskrete Zufallsgröße $z = 1$. Für einen zweiten Zufallswert $x = 0.95$ würde die Funktion dagegen das Ergebnis $z = 2$ liefern.
Aus Verständnisgründen wurde hier eine umständliche Programmierung gewählt. Der angegebene C-Programmteil könnte auch kompakter geschrieben werden:
- $$\text{\{ float random(); return((long) (random()*M)); \} }$$
Aufgaben zum Kapitel
Aufgabe 2.6: PN-Generator der Länge 5
Aufgabe 2.6Z: PN-Generator der Länge 3
Aufgabe 2.7: C-Programme z1 und z2
Zusatzaufgabe 2.7Z: C-Programm z3