Aufgaben:Aufgabe 3.2: VTF zur Aufgabe 3.1

• Zurück zum Buch

Cosinus–Quadrat–VTF (oben),
Dirac–VTF (unten)

Es gelten die gleichen Voraussetzungen wie für die  Aufgabe 3.1.

• Die WDF der wertkontinuierlichen Zufallsgröße ist in den Bereichen  $|x| > 2$  identisch Null,  und im Bereich  $-2 \le x \le +2$  gilt:

$$f_x(x)={1}/{2}\cdot \cos^2({\pi}/{4}\cdot x).$$

• Auch die diskrete Zufallsgröße  $y$  ist auf den Bereich  $\pm 2$  begrenzt.  Hier gelten folgende Wahrscheinlichkeiten:

$${\rm \Pr}(y=0)=0.4,$$

$${\rm \Pr}(y=+1)={\rm \Pr}(y=-1)=0.2,$$

$${\rm \Pr}(y=+2)={\rm \Pr}(y=-2)=0.1.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Verteilungsfunktion.

• Gegeben ist die folgende Gleichung:

$$\int \cos^{\rm 2}( ax)\, {\rm d}x=\frac{x}{2}+\frac{1}{4 a}\cdot \sin(2 ax).$$

• Eine Zusammenfassung der hier behandelten Thematik bietet das Lernvideo  Zusammenhang zwischen WDF und VTF.

Fragebogen

1

Welche der folgenden Aussagen sind für die Verteilungsfunktion  $F_x(r)$  der wertkontinuierlichen Zufallsgröße  $x$  richtig?

	Die VTF ist für alle Werte  $r \le -2$  gleich  $F_x(r) \equiv 0$.
	Die VTF ist für alle Werte  $r \ge +2$  gleich  $F_x(r) \equiv 1$.
	Der Verlauf von  $F_x(r)$  ist monoton steigend.

2

Welche der folgenden Aussagen sind für die Verteilungsfunktion  $F_y(r)$  der wertdiskreten Zufallsgröße  $y$  richtig?

	Die VTF ist für alle Werte  $r \le -2$  gleich  $F_y(r) \equiv 0$.
	Die VTF ist für alle Werte  $r \ge +2$  gleich  $F_y(r) \equiv 1$.
	Der Verlauf von  $F_y(r)$  ist monoton steigend.

3

Berechnen Sie die Verteilungsfunktion  $F_x(r)$.  Beschränken Sie sich hier auf den Bereich  $0 \le r \le +2$.
Welcher Wert ergibt sich für  $r = +1$?

$F_x(r=+1) \ = \ $

4

Welcher Zusammenhang besteht zwischen  $F_x(r)$  und  $F_x(-r)$?  Geben Sie den VTF-Wert  $F_x(r=-1)$  ein.

$F_x(r=-1) \ = \ $

5

Berechnen Sie die Wahrscheinlichkeit, dass  $x$  betragsmäßig kleiner als  $1$  ist.
Vergleichen Sie das Resultat mit dem Ergebnis der Teilaufgabe  (7)  von Aufgabe 3.1.

${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}| < 1) \ = \ $

6

Welchen Wert erhält man für die Verteilungsfunktion der diskreten Zufallsgröße  $y$  an der Stelle  $r = 0$?

$F_y(r = 0)\ = \ $

Musterlösung

Musterlösung

(1)  Da  $x$  eine kontinuierliche Zufallsgröße und auf den Bereich  $|\hspace{0.05cm}x\hspace{0.05cm}< 2|$  begrenzt ist, sind alle drei vorgegebenen Aussagen richtig.

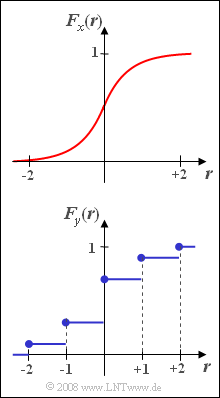
(2)  Richtig sind hier nur die Aussagen 2 und 3:

• Bei einer diskreten Zufallsgröße steigt die Verteilungsfunktion nur schwach monoton an.
• Das heißt:   Es gibt außer Sprüngen ausschließlich horizontale Abschnitte der VTF.
• Da an den Sprungstellen jeweils der rechtsseitige Grenzwert gilt, ist demzufolge  $F_y(-2) = 0.1$, also ungleich Null.

(3)  Die VTF  $F_x(r)$  berechnet sich als das Integral von  $-\infty$  bis  $r$  über die WDF  $f_x(x)$.

Aufgrund der Symmetrie kann hierfür im Bereich  $0 \le r \le +2$  geschrieben werden:

$$F_{x} (r) =\frac{1}{2} + \int_{0}^{r} f_x(x)\;{\rm d}x = \frac{1}{2} + \int_{0}^{ r} {1}/{2}\cdot \cos^2 ({\pi}/{4}\cdot x)\;{\rm d}x.$$

In gleicher Weise wie bei der Teilaufgabe  (7)  der Aufgabe 3.1 erhält man somit:

$$F_{x} (r) =\frac{1}{2} + \frac{ r}{ 4} + \frac{1}{2 \pi} \cdot \sin({\pi}/{2}\cdot r),$$

$$F_{x} (r=0) =\rm \frac{1}{2} + \rm \frac{1}{2 \pi} \cdot\rm sin(\rm 0)\hspace{0.15cm}{= 0.500},$$

$$F_{x} (r=1) =\rm \frac{1}{2} + \frac{\rm 1}{\rm 4} + \rm \frac{1}{2 \pi}\cdot \rm sin({\pi}/{2})\hspace{0.15cm}\underline{=0.909},$$

$$F_{x} (r=2) =\rm \frac{1}{2} + \frac{\rm1}{\rm 2} + \rm \frac{1}{2 \pi} \cdot \rm sin(\pi)\hspace{0.15cm}{= 1.000}.$$

(4)  Aufgrund der Punktsymmetrie um  $r=0$   bzw.  $F_{x} (0) = 1/2$  und wegen  $\sin(-x) = -\sin(x)$  gilt diese Formel im gesamten Bereich, wie die folgende Kontrollrechnung zeigt:

$$F_{x} (r=-2) =\rm \frac{1}{2} - \frac{\rm1}{\rm 2} - \rm \frac{1}{2 \pi} \cdot\rm sin(\pi)=0,$$

$$F_{x} (r=-1) =\rm \frac{1}{2} - \frac{\rm1}{\rm 4} - \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2})\hspace{0.15cm}\underline{= 0.091}.$$

(5)  Für die Wahrscheinlichkeit, dass  $x$  zwischen  $-1$  und  $+1$  liegt, gilt:

$${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}|< 1)= F_{x}(+1) - F_{ x}(-1)= 0.909-0.091\hspace{0.15cm}\underline{= 0.818}.$$

• Dieses Ergebnis stimmt exakt mit dem Resultat der Teilaufgabe  (7)  der Aufgabe 3.1 überein, das durch direkte Integration über die WDF ermittelt wurde.

(6)  Die VTF der diskreten Zufallsgröße  $y$  an der Stelle  $y =0$  ist die Summe der Wahrscheinlichkeiten von  $-2$,  $-1$  und  $0$,  also gilt

$$F_y(r = 0)\hspace{0.15cm}\underline{= 0.7}.$$