Aufgaben:Aufgabe 4.8: Rautenförmige 2D-WDF

• Zurück zum Buch

Rautenförmige 2D-WDF

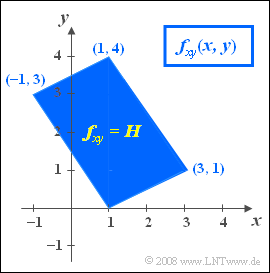
Wir betrachten eine 2D–Zufallsgröße  $(x, y)$, deren Komponenten sich jeweils als Linearkombinationen zweier Zufallsgrößen  $u$  und  $v$  ergeben:

$$x=2u-2v+1,$$

$$y=u+3v.$$

Weiter ist zu beachten:

• Die zwei statistisch unabhängigen Zufallsgrößen  $u$  und  $v$  sind jeweils gleichverteilt zwischen  $0$  und  $1$.
• In der Abbildung sehen Sie die 2D–WDF.  Innerhalb des blau eingezeichneten Parallelogramms gilt:

$$f_{xy}(x, y) = H = {\rm const.}$$

• Außerhalb des Parallelogramms sind keine Werte möglich:   $f_{xy}(x, y) = 0$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Linearkombinationen von Zufallsgrößen.
• Bezug genommen wird auch auf die Seite  Korrelationsgerade.
• Wir verweisen hier auch auf das interaktive Applet  Korrelationskoeffizient und Regressionsgerade.
• Gehen Sie - wenn möglich - von den angegebenen Gleichungen aus.  Nutzen Sie die Informationen der obigen Skizze vorwiegend nur zur Kontrolle Ihrer Ergebnisse.

Fragebogen

1

Wie groß ist die Höhe  $H$  der 2D–WDF innerhalb des Parallelogramms?

$H \ = \ $

2

Welche Werte von  $u$  und  $v$  liegen dem Eckpunkt  $(-1, 3)$  zugrunde?

$u \ = \ $

$v \ = \ $

3

Berechnen Sie den Korrelationskoeffizienten  $\rho_{xy}$.

$\rho_{xy}\ = \ $

4

Wie lautet die Korrelationsgerade  $y=K(x)$?  Bei welchem Punkt  $y_0$  schneidet diese die  $y$-Achse?

$y_0\ = \ $

5

Berechnen Sie die Randwahrscheinlichkeitsdichtefunktion $f_x(x)$.  Wie groß ist die Wahrscheinlichkeit, dass die Zufallsgröße  $x$  negativ ist?

${\rm Pr}(x < 0)\ = \ $

6

Berechnen Sie die Randwahrscheinlichkeitsdichtefunktion $f_y(y)$.  Wie groß ist die Wahrscheinlichkeit, dass die Zufallsgröße  $y >3$  ist?

${\rm Pr}(y > 3)\ = \ $

Musterlösung

Musterlösung

(1)  Die Fläche des Parallelogramms kann aus zwei gleich großen Dreiecken zusammengesetzt werden.

• Die Fläche des Dreiecks $(1,0)\ (1,4)\ (-1,3)$ ergibt $0.5 · 4 · 2 = 4$.
• Die Gesamtfläche ist doppelt so groß:   $F = 8$.
• Da das WDF-Volumen stets $1$ ist, gilt $H= 1/F\hspace{0.15cm}\underline{ = 0.125}$.

(2)  Der minimale Wert von $x$  ergibt sich für $\underline{ u=0}$ und $\underline{ v=1}$. Daraus folgen aus obigen Gleichungen die Ergebnisse $x= -1$ und $y= +3$.

(3)  Die im Theorieteil angegebene Gleichung gilt allgemein, d. h. für jede beliebige WDF der beiden statistisch unabhängigen Größen $u$ und $v$, so lange diese gleiche Streuungen aufweisen $(\sigma_u = \sigma_v)$.

Mit $A = 2$, $B = -2$, $D = 1$ und $E = 3$ erhält man:

$$\rho_{xy } = \frac {\it A \cdot D + B \cdot E}{\sqrt{(\it A^{\rm 2}+\it B^{\rm 2})(\it D^{\rm 2}+\it E^{\rm 2})}} =\frac {2 \cdot 1 -2 \cdot 3}{\sqrt{(4 +4)(1+9)}} = \frac {-4}{\sqrt{80}} = \frac {-1}{\sqrt{5}}\hspace{0.15cm}\underline{ = -0.447}. $$

(4)  Die Korrelationsgerade lautet allgemein:

$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x-m_x)+m_y.$$

• Aus den linearen Mittelwerten $m_u = m_v = 0.5$ und den in der Aufgabenstellung angegebenen Gleichungen erhält man $m_x = 1$ und $m_y = 2$.

• Die Varianzen von $u$ und $v$ betragen jeweils $\sigma_u^2 = \sigma_v^2 =1/12$. Daraus folgt:

$$\sigma_x^2 = 4 \cdot \sigma_u^2 + 4 \cdot \sigma_v^2 = 2/3,$$

$$\sigma_y^2 = \sigma_u^2 + 9\cdot \sigma_v^2 = 5/6.$$

• Setzt man diese Werte in die Gleichung der Korrelationsgeraden ein, so ergibt sich:

$$y=K(x)=\frac{\sqrt{5/6}}{\sqrt{2/3}}\cdot (\frac{-1}{\sqrt{5}})\cdot(x-1)+2= - x/{2} + 2.5.$$

• Daraus folgt der Wert $y_0\hspace{0.15cm}\underline{ = 2.5}$

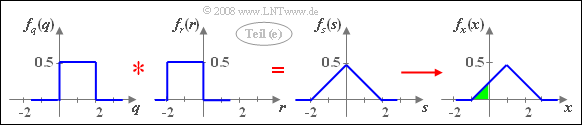
(5)  Mit den Hilfsgrößen   $q= 2u$,   $r= -2v$   und   $s= x-1$ gilt der Zusammenhang:   $s= q+r$.

• Da $u$  und $v$  jeweils zwischen $0$ und $1$ gleichverteilt sind, besitzt $q$ eine Gleichverteilung im Bereich von $0$ bis $2$ und $r$ eine Gleichverteilung zwischen $-2$ und $0$.

• Da zudem $q$ und $r$ nicht statistisch voneinander abhängen, gilt für die WDF der Summe:

Dreieckförmige WDF $f_x(x)$

$$f_s(s) = f_q(q) \star f_r(r).$$

• Die Addition$x = s+1$ führt zu einer Verschiebung der Dreieck–WDF um $1$ nach rechts.
• Für die gesuchte Wahrscheinlichkeit (im folgenden Bild grün hinterlegt) gilt deshalb: ${\rm Pr}(x < 0)\hspace{0.15cm}\underline{ = 0.125}$.

Trapezförmige WDF $f_y(y)$

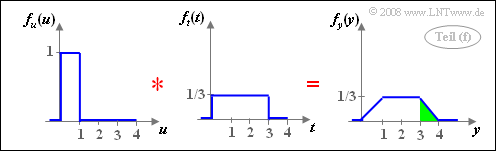
(6)  Analog zur Musterlösung für die Teilaufgabe (5) gilt mit $t = 3v$:

$$f_y(y) = f_u(u) \star f_t(t).$$

• Die Faltung zwischen zwei verschieden breiten Rechtecken ergibt ein Trapez.
• Für die gesuchte Wahrscheinlichkeit erhält man ${\rm Pr}(y>3) =1/6\hspace{0.15cm}\underline{ \approx 0.167}$.
• Diese Wahrscheinlichkeit ist in der rechten Skizze grün hinterlegt.