Aufgaben:Aufgabe 2.11: Arithmetische Codierung: Unterschied zwischen den Versionen
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID2468__Inf_A_2_11.png|right|frame|Intervallschachtelung bei <br>arithmetischer Codierung]] | [[Datei:P_ID2468__Inf_A_2_11.png|right|frame|Intervallschachtelung bei <br>arithmetischer Codierung]] | ||
| − | Die arithmetische Codierung ist eine spezielle Form der Entropiecodierung: Die Symbolwahrscheinlichkeiten müssen auch hier bekannt sein. In dieser Aufgabe gehen wir von $M = 3$ Symbolen aus, die wir mit $\rm X$, $\rm Y$ und $\rm Z$ benennen. | + | Die arithmetische Codierung ist eine spezielle Form der Entropiecodierung: Die Symbolwahrscheinlichkeiten müssen auch hier bekannt sein. In dieser Aufgabe gehen wir von $M = 3$ Symbolen aus, die wir mit $\rm X$, $\rm Y$ und $\rm Z$ benennen. |
| − | Während die Huffman–Codierung symbolweise erfolgt, wird bei der Arithmetischen Codierung ( | + | Während die Huffman–Codierung symbolweise erfolgt, wird bei der Arithmetischen Codierung $(\rm AC)$ eine Symbolfolge der Länge $N$ gemeinsam codiert. Das Codierergebnis ist ein reeller Zahlenwert $r$ aus dem Intervall |
| − | :$$I = \big[B, E \big) = \big[B, B +{\it \Delta} \big)\hspace{0.05cm}.$$ | + | :$$I = \big[B, \ E \big) = \big[B, \ B +{\it \Delta} \big)\hspace{0.05cm}.$$ |
Diese Notation bedeutet: | Diese Notation bedeutet: | ||
| − | * Der Beginn $B$ gehört zum Intervall $I$. | + | * Der Beginn $B$ gehört zum Intervall $I$. |
| − | * Das Ende $E$ ist nicht mehr in $I$ enthalten. | + | * Das Ende $E$ ist nicht mehr in $I$ enthalten. |
| − | * Die Intervallbreite ist ${\it} \Delta = E - B$. | + | * Die Intervallbreite ist ${\it} \Delta = E - B$. |
| − | Von den unendlich vielen möglichen Werten $r \in I$ (da $r$ reellwertig ist, also kein Integer) wird derjenige Zahlenwert ausgewählt, der mit der geringsten Bitanzahl auskommt. Hierzu zwei Beispiele zur Verdeutlichung: | + | Von den unendlich vielen möglichen Werten $r \in I$ $($da $r$ reellwertig ist, also kein Integer$)$ wird derjenige Zahlenwert ausgewählt, der mit der geringsten Bitanzahl auskommt. Hierzu zwei Beispiele zur Verdeutlichung: |
| − | * Der Dezimalwert $r = 3/4$ lässt sich mit zwei Bit darstellen: | + | * Der Dezimalwert $r = 3/4$ lässt sich mit zwei Bit darstellen: |
:$$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} | :$$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} | ||
| − | \Rightarrow\hspace{0.3cm}\text{binär:}\hspace{0. | + | \Rightarrow\hspace{0.3cm}\text{binär:}\hspace{0.25cm} 0.11\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text |
| − | {Code:} \hspace{0. | + | {Code:} \hspace{0.25cm} \boldsymbol{\rm 11} \hspace{0.05cm}, $$ |
| − | * Der Dezimalwert $r = 1/3$ benötigt dagegen unendlich viele Bit: | + | * Der Dezimalwert $r = 1/3$ benötigt dagegen unendlich viele Bit: |
:$$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}\text{...}$$ | :$$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}\text{...}$$ | ||
:$$ | :$$ | ||
| − | \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0. | + | \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0.25cm}0.011101\hspace{0.3cm}\Rightarrow\hspace{0.3cm} |
| − | \text{Code:} \hspace{0. | + | \text{Code:} \hspace{0.25cm} \boldsymbol{\rm 011101} \hspace{0.05cm}. $$ |
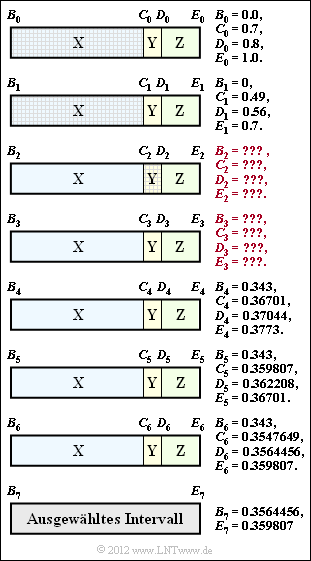
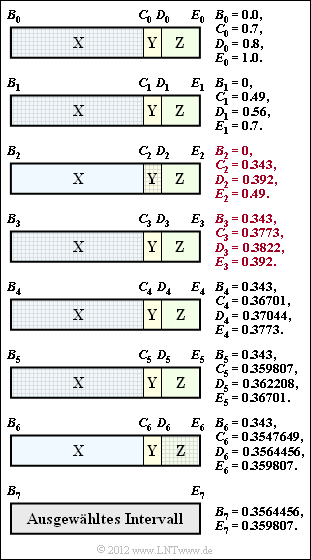
In dieser Aufgabe beschränken wir uns auf die Bestimmung des aktuellen Intervalls $I$, gekennzeichnet durch den Beginn $B$ sowie dem Ende $E$ bzw. der Breite $\Delta$. | In dieser Aufgabe beschränken wir uns auf die Bestimmung des aktuellen Intervalls $I$, gekennzeichnet durch den Beginn $B$ sowie dem Ende $E$ bzw. der Breite $\Delta$. | ||
*Diese Bestimmung geschieht entsprechend der Intervallschachtelung in obiger Grafik. | *Diese Bestimmung geschieht entsprechend der Intervallschachtelung in obiger Grafik. | ||
| − | *An der Schraffierung ist zu erkennen, dass die Folge mit den Ternärsymbolen $\rm XXY$ beginnt. | + | *An der Schraffierung ist zu erkennen, dass die Folge mit den Ternärsymbolen $\rm XXY$ beginnt. |
<br clear=all> | <br clear=all> | ||
Der Algorithmus funktioniert wie folgt: | Der Algorithmus funktioniert wie folgt: | ||
| − | * Vor Beginn (quasi beim nullten Symbol) wird der gesamte Wahrscheinlichkeitsbereich nach den Wahrscheinlichkeiten $p_{\rm X}$, $p_{\rm Y}$ und $p_{\rm Z}$ in drei Bereiche unterteilt. Die Grenzen liegen bei | + | * Vor Beginn (quasi beim nullten Symbol) wird der gesamte Wahrscheinlichkeitsbereich nach den Wahrscheinlichkeiten $p_{\rm X}$, $p_{\rm Y}$ und $p_{\rm Z}$ in drei Bereiche unterteilt. Die Grenzen liegen bei |
| − | :$$B_0 = 0\hspace{0.05cm},\hspace{0. | + | :$$B_0 = 0\hspace{0.05cm},\hspace{0.4cm}C_0 = p_{\rm X}\hspace{0.05cm},\hspace{0.4cm}D_0 = p_{\rm X} + p_{\rm Y}\hspace{0.05cm},\hspace{0.4cm} E_0 = p_{\rm X} + p_{\rm Y}+ p_{\rm Z} = 1\hspace{0.05cm}.$$ |
| − | * Das erste Symbol der zu codierenden Folge ist $\rm X$ | + | * Das erste Symbol der zu codierenden Folge ist $\rm X$. Das bedeutet: das ausgewählte Intervall wird durch $B_0$ und $C_0$ begrenzt. Dieses Intervall wird mit neuem Beginn $B_1 = B_0$ und neuem Ende $E_1 = C_0$ in gleicher Weise aufgeteilt wie der Gesamtbereich im nullten Schritt. Die Zwischenwerte sind $C_1$ und $D_1$. |
| − | * Die weitere Intervall–Aufteilung ist Ihre Aufgabe. Beispielsweise sollen in der Teilaufgabe '''(2)''' die Grenzen $B_2$, $C_2$, $D_2$ und $E_2$ für das zweite Symbol $\rm X$ ermittelt werden und in der Teilaufgabe '''(3)''' die Grenzen $B_3$, $C_3$, $D_3$ und $E_3$ für das dritte Symbol $\rm Y$. | + | * Die weitere Intervall–Aufteilung ist Ihre Aufgabe. Beispielsweise sollen in der Teilaufgabe '''(2)''' die Grenzen $B_2$, $C_2$, $D_2$ und $E_2$ für das zweite Symbol $\rm X$ ermittelt werden und in der Teilaufgabe '''(3)''' die Grenzen $B_3$, $C_3$, $D_3$ und $E_3$ für das dritte Symbol $\rm Y$. |
| Zeile 41: | Zeile 41: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. |
| − | *Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren#Arithmetische_Codierung|Arithmetische Codierung]]. | + | *Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren#Arithmetische_Codierung|Arithmetische Codierung]]. |
| − | *Die Binärdarstellung des ausgewählten Intervalls wird in der [[Aufgaben:Aufgabe_2.11:_Nochmals_Arithmetische_Codierung|Aufgabe 2.11Z]] behandelt. | + | *Die Binärdarstellung des ausgewählten Intervalls wird in der [[Aufgaben:Aufgabe_2.11:_Nochmals_Arithmetische_Codierung|Aufgabe 2.11Z]] behandelt. |
| Zeile 51: | Zeile 51: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Wahrscheinlichkeiten | + | {Welche Wahrscheinlichkeiten liegen der Grafik zugrunde? |
|type="{}"} | |type="{}"} | ||
$p_{\rm X} \hspace{0.10cm} = \ $ { 0.7 3% } | $p_{\rm X} \hspace{0.10cm} = \ $ { 0.7 3% } | ||
| Zeile 58: | Zeile 58: | ||
| − | {Wie lauten die Bereichsgrenzen nach der Codierung des zweiten Symbols $\rm X$? | + | {Wie lauten die Bereichsgrenzen nach der Codierung des zweiten Symbols $\rm X$? |
|type="{}"} | |type="{}"} | ||
$B_2 \hspace{0.12cm} = \ $ { 0. } | $B_2 \hspace{0.12cm} = \ $ { 0. } | ||
| Zeile 66: | Zeile 66: | ||
| − | {Wie lauten die Bereichsgrenzen nach der Codierung des dritten Symbols $\rm Y$? | + | {Wie lauten die Bereichsgrenzen nach der Codierung des dritten Symbols $\rm Y$? |
|type="{}"} | |type="{}"} | ||
$B_3 \hspace{0.12cm} = \ $ { 0.343 1% } | $B_3 \hspace{0.12cm} = \ $ { 0.343 1% } | ||
| Zeile 74: | Zeile 74: | ||
| − | {Nach der Codierung des vierten Symbols ist $B_4 = 0.343$. Was folgt daraus? | + | {Nach der Codierung des vierten Symbols ist $B_4 = 0.343$. Was folgt daraus? |
| − | |type=" | + | |type="()"} |
| − | + Das vierte Symbol war $\rm X$. | + | + Das vierte Symbol war $\rm X$. |
| − | - Das vierte Symbol war $\rm Y$. | + | - Das vierte Symbol war $\rm Y$. |
| − | - Das vierte Symbol war $\rm Z$. | + | - Das vierte Symbol war $\rm Z$. |
| − | {Nach weiteren Symbolen wird das Intervall durch $B_7 = 0.3564456$ und $E_7 = 0.359807$ begrenzt. Welche Aussagen treffen zu? | + | {Nach weiteren Symbolen wird das Intervall durch $B_7 = 0.3564456$ und $E_7 = 0.359807$ begrenzt. Welche Aussagen treffen zu? |
|type="[]"} | |type="[]"} | ||
| − | - Die zur Codierung anstehende Symbolfolge lautet $\rm XXYXXZX$. | + | - Die zur Codierung anstehende Symbolfolge lautet $\rm XXYXXZX$. |
| − | + Die zur Codierung anstehende Symbolfolge lautet $\rm XXYXXXZ$. | + | + Die zur Codierung anstehende Symbolfolge lautet $\rm XXYXXXZ$. |
| − | + Die Breite des resultierenden Intervalls ist ${\it \Delta} = p_{\rm X}^5 \cdot p_{\rm Y} \cdot p_{\rm Z}$. | + | + Die Breite des resultierenden Intervalls ist ${\it \Delta} = p_{\rm X}^5 \cdot p_{\rm Y} \cdot p_{\rm Z}$. |
Version vom 28. Januar 2020, 14:05 Uhr
Die arithmetische Codierung ist eine spezielle Form der Entropiecodierung: Die Symbolwahrscheinlichkeiten müssen auch hier bekannt sein. In dieser Aufgabe gehen wir von $M = 3$ Symbolen aus, die wir mit $\rm X$, $\rm Y$ und $\rm Z$ benennen.
Während die Huffman–Codierung symbolweise erfolgt, wird bei der Arithmetischen Codierung $(\rm AC)$ eine Symbolfolge der Länge $N$ gemeinsam codiert. Das Codierergebnis ist ein reeller Zahlenwert $r$ aus dem Intervall
- $$I = \big[B, \ E \big) = \big[B, \ B +{\it \Delta} \big)\hspace{0.05cm}.$$
Diese Notation bedeutet:
- Der Beginn $B$ gehört zum Intervall $I$.
- Das Ende $E$ ist nicht mehr in $I$ enthalten.
- Die Intervallbreite ist ${\it} \Delta = E - B$.
Von den unendlich vielen möglichen Werten $r \in I$ $($da $r$ reellwertig ist, also kein Integer$)$ wird derjenige Zahlenwert ausgewählt, der mit der geringsten Bitanzahl auskommt. Hierzu zwei Beispiele zur Verdeutlichung:
- Der Dezimalwert $r = 3/4$ lässt sich mit zwei Bit darstellen:
- $$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\text{binär:}\hspace{0.25cm} 0.11\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text {Code:} \hspace{0.25cm} \boldsymbol{\rm 11} \hspace{0.05cm}, $$
- Der Dezimalwert $r = 1/3$ benötigt dagegen unendlich viele Bit:
- $$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}\text{...}$$
- $$ \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0.25cm}0.011101\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \text{Code:} \hspace{0.25cm} \boldsymbol{\rm 011101} \hspace{0.05cm}. $$
In dieser Aufgabe beschränken wir uns auf die Bestimmung des aktuellen Intervalls $I$, gekennzeichnet durch den Beginn $B$ sowie dem Ende $E$ bzw. der Breite $\Delta$.
- Diese Bestimmung geschieht entsprechend der Intervallschachtelung in obiger Grafik.
- An der Schraffierung ist zu erkennen, dass die Folge mit den Ternärsymbolen $\rm XXY$ beginnt.
Der Algorithmus funktioniert wie folgt:
- Vor Beginn (quasi beim nullten Symbol) wird der gesamte Wahrscheinlichkeitsbereich nach den Wahrscheinlichkeiten $p_{\rm X}$, $p_{\rm Y}$ und $p_{\rm Z}$ in drei Bereiche unterteilt. Die Grenzen liegen bei
- $$B_0 = 0\hspace{0.05cm},\hspace{0.4cm}C_0 = p_{\rm X}\hspace{0.05cm},\hspace{0.4cm}D_0 = p_{\rm X} + p_{\rm Y}\hspace{0.05cm},\hspace{0.4cm} E_0 = p_{\rm X} + p_{\rm Y}+ p_{\rm Z} = 1\hspace{0.05cm}.$$
- Das erste Symbol der zu codierenden Folge ist $\rm X$. Das bedeutet: das ausgewählte Intervall wird durch $B_0$ und $C_0$ begrenzt. Dieses Intervall wird mit neuem Beginn $B_1 = B_0$ und neuem Ende $E_1 = C_0$ in gleicher Weise aufgeteilt wie der Gesamtbereich im nullten Schritt. Die Zwischenwerte sind $C_1$ und $D_1$.
- Die weitere Intervall–Aufteilung ist Ihre Aufgabe. Beispielsweise sollen in der Teilaufgabe (2) die Grenzen $B_2$, $C_2$, $D_2$ und $E_2$ für das zweite Symbol $\rm X$ ermittelt werden und in der Teilaufgabe (3) die Grenzen $B_3$, $C_3$, $D_3$ und $E_3$ für das dritte Symbol $\rm Y$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Quellencodierverfahren.
- Insbesondere wird Bezug genommen auf die Seite Arithmetische Codierung.
- Die Binärdarstellung des ausgewählten Intervalls wird in der Aufgabe 2.11Z behandelt.
Fragebogen
Musterlösung
(1) Aus der Grafik auf der Angabenseite kann man die Wahrscheinlichkeiten ablesen:
- $$p_{\rm X} = 0.7\hspace{0.05cm},\hspace{0.2cm}p_{\rm Y} = 0.1\hspace{0.05cm},\hspace{0.2cm}p_{\rm Z} = 0.2\hspace{0.05cm}.$$
(2) Auch das zweite Symbol ist $\rm X$. Bei gleichem Vorgehen wie in der Aufgabenbeschreibung erhält man
- $$B_2 \hspace{0.1cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}C_2 = 0.49 \cdot 0.7 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm} D_2 \hspace{0.1cm} \underline{= 0.392}\hspace{0.05cm},\hspace{0.2cm}E_2 = C_1 \hspace{0.1cm}\underline{= 0.49} \hspace{0.05cm}.$$
(3) Für das dritte Symbol $\rm Y$ gelten nun die Begrenzungen $B_3 = C_2$ und $E_3 = D_2$:
- $$B_3 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm}C_3 \hspace{0.1cm}\underline{= 0.3773}\hspace{0.05cm},\hspace{0.2cm} D_3 \hspace{0.1cm} \underline{= 0.3822}\hspace{0.05cm},\hspace{0.2cm}E_3 \hspace{0.1cm}\underline{= 0.392} \hspace{0.05cm}.$$
(4) Richtig ist der Lösungsvorschlag 1:
- Aus $B_4 = 0.343 = B_3$ (abzulesen in der Grafik auf dem Angabenblatt) folgt zwingend, dass das vierte Quellensymbol ein $\rm X$ war.
(5) Richtig sind die Lösungsvorschläge 2 und 3:
- Die Grafik zeigt die Intervallschachtelung mit allen bisherigen Ergebnissen. Man erkennt aus der Schraffierung, dass der zweite Lösungsvorschlag die richtige Symbolfolge angibt: $\rm XXYXXXZ$.
- Die Intervallbreite $\it \Delta$ kann wirklich gemäß dem Vorschlag 3 ermittelt werden. Es gilt:
- $${\it \Delta} = 0.359807 - 0.3564456 = 0.003614 \hspace{0.05cm},$$
- $${\it \Delta} =p_{\rm X}^5 \cdot p_{\rm Y} \cdot p_{\rm Z} = 0.7^5 \cdot 0.1 \cdot 0.2 = 0.003614 \hspace{0.05cm}. $$
(6) Richtig ist der Lösungsvorschlag 2 ⇒ $r_2 = (0.010111)_{\text{binär}}$, wegen:
- $$r_2 = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 0 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 1 \cdot 2^{-5} + 1 \cdot 2^{-6} = 0.359375\hspace{0.05cm}. $$
- Der Vorschlag 1: $r_1 = (0.101100)_{\text{binär}}$ ist auszuschließen, da der zugehörige Dezimalwert $r_1 > 0.5$ ist.
- Auch der letzte Lösungsvorschlag ist falsch, da $r_3 = (0.001011)_{\text{binär}} < (0.01)_{\text{binär}} = (0.25)_{\text{dezimal}}$ ergibt.