Applets:Korrelation und Regressionsgerade: Unterschied zwischen den Versionen
| Zeile 175: | Zeile 175: | ||
'''(3)''' Es gelten zunächst weiter die Einstellungen von '''(2)'''. Wie ändern sich die Ergebnisse nach Variation des Parameters $p_1$ im erlaubten Bereich $(0\le p_1 \le 0.5)$?}} | '''(3)''' Es gelten zunächst weiter die Einstellungen von '''(2)'''. Wie ändern sich die Ergebnisse nach Variation des Parameters $p_1$ im erlaubten Bereich $(0\le p_1 \le 0.5)$?}} | ||
| − | ::* Die blaue Regressionsgerade verläuft weiter unter dem Winkel $ \theta_{X \to Y}= 45^\circ$. Das heißt: es gilt hier $\mu_{XY} =\sigma_Y^2$, und zwar unabhängig von $p_1$. | + | ::* Die blaue Regressionsgerade verläuft weiter unter dem Winkel $ \theta_{X \to Y}= 45^\circ$. Das heißt: es gilt hier $\mu_{XY} =\sigma_Y^2$, und zwar unabhängig von $p_1 < 0.5$. |
| + | ::* Im Grenzfall $p_1 = 0.5$ ist wegen $\sigma_Y =0$ die blaue Regressionsgerade undefiniert. Es handelt sich nurmehr um eine 1D–Zufallsgröße $X$. | ||
::* Mit $p_1=0$ sind nur die äußeren Punkte $3$ und $4$ wirksam ⇒ $ \theta_{Y \to X}= \theta_{X \to Y}= 45^\circ$, mit $p_1=0.5$ nur die inneren Punkte $1$ und $2$ ⇒ $ \theta_{Y \to X}= 0^\circ$. | ::* Mit $p_1=0$ sind nur die äußeren Punkte $3$ und $4$ wirksam ⇒ $ \theta_{Y \to X}= \theta_{X \to Y}= 45^\circ$, mit $p_1=0.5$ nur die inneren Punkte $1$ und $2$ ⇒ $ \theta_{Y \to X}= 0^\circ$. | ||
::* Dazwischen wird die rote Regressionsgerade kontinuierlich flacher. Sind alle Punkte gleichwahrscheinlich $(p_1=0.25)$, dann ist $\theta_{Y \to X}\approx 38.7^\circ$. | ::* Dazwischen wird die rote Regressionsgerade kontinuierlich flacher. Sind alle Punkte gleichwahrscheinlich $(p_1=0.25)$, dann ist $\theta_{Y \to X}\approx 38.7^\circ$. | ||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(4)''' | + | '''(4)''' Nun gelte $x_1 = 0,\ y_1 = 0.5,\ p_1 = 0.3$. Variieren Sie $p_1$ im Bereich $0\le p_1 < 0.5$ und interpretieren Sie die Ergebnisse. $(p_1 = 0.5)$ sollte man ausschließen.}} |
| − | |||
| − | |||
| − | |||
| − | $\ | ||
| − | $\ | + | ::* Wegen $\sigma_X \le \sigma_Y$ liegt weiterhin die blaue Gerade nie unterhalb der roten, die nun für alle $p_1 \ne 0.5$ die Winkelhalbierende ist ⇒ $ \theta_{Y \to X}\approx 45^\circ$. |
| + | ::* Der Winkel der blauen Regressionsgerade wächst von $ \theta_{X \to Y}= 45^\circ \ (p_1 = 0)$ bis $ \theta_{X \to Y} \to 45^\circ \ (p_1 \to 0.5)$ kontinuierlich an. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(5)''' | + | '''(5)''' Beginnen Sie mit $x_1 = 0.8,\ y_1 = -0.8,\ p_1 = 0.25$ vergrößern Sie $y_1$ bis zum Endwert $y_1 = +0.8$. Interpretieren Sie die Ergebnisse.}} |
| − | + | ::* Für $y_1 =-0.8$ ist $ \theta_{X \to Y}= 77.6^\circ$ und $ \theta_{Y \to X}= 12.4^\circ$. Mit steigendem $y_1$ verläuft die blaue Gerade $ R_{X \to Y}$ flacher und die rote $ (R_{Y \to X})$ steiler. | |
| − | $ | + | ::* Im Endpunkt $(y_1 = +0.8)$ verlaufen die beiden Regressionsgeraden deckungsgleich unter dem Winkel $ \theta_{X \to Y}= \theta_{Y \to X}= 45^\circ$. |
| − | |||
| − | $ | ||
| − | |||
| − | $\ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(6)''' | + | '''(6)''' Abschließend gelte $x_1 = +1,\ y_1 = -1$. Variieren Sie $p_1$ im gesamten zulässigen Bereich $0\le p_1 \le 0.5$. Wann sind die beiden Zufallsgrößen unkorreliert?}} |
| − | |||
| − | $\ | + | ::* Für $p_1 = 0$ gilt $ \theta_{X \to Y}=\theta_{Y \to X}= 45^\circ.$ Anschließend dreht die blaue Gerade entgegen dem Uhrzeigersinn und die rote Gerade im Uhrzeigersinn. |
| + | ::* Für $p_1 = 0.25$ sind die Winkel $ \theta_{X \to Y}=90^\circ, \ \theta_{Y \to X}= 0^\circ.$ Diese Momentaufnahme trifft genau den Fall unkorrelierter Zufallsgrößen ⇒ $\mu_{XY}=0$. | ||
| + | ::* Anschließend drehen beide Geraden weiter in gleicher Richtung. Für $p_1 = 0.5$ gilt schließlich: $ \theta_{X \to Y}=135^\circ= -45^\circ, \ \theta_{Y \to X}= -45^\circ.$ | ||
| − | |||
==Zur Handhabung des Applets== | ==Zur Handhabung des Applets== | ||
Version vom 5. März 2020, 18:03 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Theoretischer Hintergrund
Erwartungswerte von 2D–Zufallsgrößen und Korrelationskoeffizient
Wir betrachten eine zweidimensionale $\rm (2D)$–Zufallsgröße $(X,\ Y)$ mit der Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ $f_{XY}(x, y)$, wobei zwischen den Einzelkomponenten $X$ und $Y$ statistische Abhängigkeiten bestehen. Ein Sonderfall ist die Korrelation.
$\text{Definition:}$ Unter Korrelation versteht man eine lineare Abhängigkeit zwischen den Einzelkomponenten $X$ und $Y$.
- Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig.
- Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.
Für das Folgende setzen wir voraus, dass $X$ und $Y$ mittelwertfrei seien ⇒ ${\rm E}\big [ X \big ] = {\rm E}\big [ Y \big ]=0$. Zur Beschreibung der Korrelation genügen dann folgende Erwartungswerte:
- die Varianzen in $X$– bzw. in $Y$–Richtung:
- $$\sigma_X^2= {\rm E}\big [ X^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}x^2 \cdot f_{X}(x) \, {\rm d}x\hspace{0.05cm},\hspace{0.5cm}\sigma_Y^2= {\rm E}\big [Y^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}y^2 \cdot f_{Y}(y) \, {\rm d}y\hspace{0.05cm};$$
- die Kovarianz zwischen den Einzelkomponenten $X$ und $Y$:
- $$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\ \cdot y \cdot f_{XY}(x,y) \, {\rm d}x\, {\rm d}y\hspace{0.05cm}.$$
Bei statististischer Unabhängigkeit der beiden Komponenten $X$ und $Y$ ist die Kovarianz $\mu_{XY} \equiv 0$.
- Das Ergebnis $\mu_{XY} = 0$ ist auch bei statistisch abhängigen Komponenten $X$ und $Y$ möglich, nämlich dann, wenn diese unkorreliert, also linear unabhängig sind.
- Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $Y=X^2.$
Man spricht dann von vollständiger Korrelation, wenn die (deterministische) Abhängigkeit zwischen $X$ und $Y$ durch die Gleichung $Y = K · X$ ausgedrückt wird.
Dann ergibt sich für die Kovarianz:
- $\mu_{XY} = σ_X · σ_Y$ bei positivem Wert von $K$,
- $\mu_{XY} = -σ_X · σ_Y$ bei negativem $K$–Wert.
Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten.
$\text{Definition:}$ Der Korrelationskoeffizient ist der Quotient aus der Kovarianz $\mu_{XY}$ und dem Produkt der Effektivwerte $σ_X$ und $σ_Y$ der beiden Komponenten:
- $$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}.$$
Der Korrelationskoeffizient $\rho_{XY}$ weist folgende Eigenschaften auf:
- Aufgrund der Normierung gilt stets $-1 \le ρ_{XY} ≤ +1$.
- Sind die beiden Zufallsgrößen $X$ und $Y$ unkorreliert, so ist $ρ_{XY} = 0$.
- Bei strenger linearer Abhängigkeit zwischen $X$ und $Y$ ist $ρ_{XY}= ±1$ ⇒ vollständige Korrelation.
- Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $X$–Wert im statistischen Mittel auch $Y$ größer ist als bei kleinerem $X$.
- Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $Y$ mit steigendem $X$ im Mittel kleiner wird.
$\text{Beispiel 1:}$ Die 2D–Zufallsgröße $(X,\ Y)$ sei diskret und kann nur vier verschiedene Werte annehmen:
- $(+0.5,\ 0)$ sowie $(-0.5,\ 0)$ jeweils mit der Wahrscheinlichkeit $0.3$,
- $(+1,\ +\hspace{-0.09cm}1)$ sowie $(-1,\ -\hspace{-0.09cm}1)$ jeweils mit der Wahrscheinlichkeit $0.2$.
$\rm (A)$ Die Varianzen bzw. die Streuungen können aus $f_{X}(x)$ und $f_{Y}(y)$ berechnet werden:
- $$\sigma_X^2 = 2 \cdot \big [0.2 \cdot 1^2 + 0.3 \cdot 0.5^2 \big] = 0.55\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_X = 0.7416,$$
- $$\sigma_Y^2 = \big [0.2 \cdot (-1)^2 + 0.6 \cdot 0^2 +0.2 \cdot (+1)^2 \big] = 0.4\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_Y = 0.6325.$$
$\rm (B)$ Für die Kovarianz ergibt sich der folgende Erwartungswert:
- $$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = 2 \cdot \big [0.2 \cdot 1 \cdot 1 + 0.3 \cdot 0.5 \cdot 0 \big] = 0.4.$$
$\rm (C)$ Damit erhält man für den Korrelationskoeffizienten:
- $$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}=\frac{0.4 } {0.7416 \cdot 0.6325 }\approx 0.8528. $$
Regressionsgerade
Ziel der linearen Regression ist es, einen einfachen (linearen) Zusammenhang zwischen zwei Zufallsgrößen $X$ und $Y$ zu anzugeben, deren $\text{2D-WDF}$ $f_{XY}(x, y)$ durch Punkte $(x_1, y_1 )$ ... $(x_N, y_N )$ in der $(x,\ y)$–Ebene vorgegeben ist. Die Skizze zeigt das Prinzip am Beispiel mittelwertfreier Größen:
- Gesucht ist die Gleichung der Geraden $K$ ⇒ $y=c_{\rm opt} \cdot x$ mit der Eigenschaft, dass der mittlere quadratische (Euklidische) Abstand $\rm (MQA)$ aller Punkte von dieser Geraden minimal ist. Man bezeichnet diese Gerade auch als Korrelationsgerade. Diese kann als eine Art „statistische Symmetrieachse“ interpretiert werden.
Bei einer großen Menge $N$ empirischer Daten ist der mathematische Aufwand beträchtlich, den bestmöglichen Parameter $C = c_{\rm opt}$ zu ermitteln. Der Aufwand wird deutlich reduziert, wenn man den Abstand nur in $x$– oder in $y$–Richtung definiert.
Im Sonderfall Gaußscher 2D-Zufallsgrößen wie in der Skizze verwendet ist die Korrelationsgerade $K$ identisch mit der Ellipsenhauptachse bei Darstellung der 2D-WDF in Form von Höhenlinien.
Stimmt das?
$\text{(a)}\hspace{0.5cm} \text{Regressionsgerade }R_{Y \to X}$ (rote Gerade in der App)
Hier wird der $y$–Wert auf den $x$–Wert zurückgeführt, was in etwa einer der möglichen Bedeutungen „Zurückfallen” des Wortes „Regression” entspricht.
- Geradengleichung, Winkel $\theta_{Y \to X}$ der Geraden $R_{Y \to X}$ zur $x$–Achse:
- $$y=C_{Y \to X} \cdot x \ \ \ \text{mit} \ \ \ C_{Y \to X}=\frac{\sigma_Y}{\sigma_X}\cdot\rho_{XY}= \frac{\mu_{XY}}{\sigma_X^2},\hspace{0.6cm} \theta_{Y \to X}={\rm arctan}\ (C_{Y \to X}).$$
- Kriterium: Der mittlere Abstand aller Punkte $(x_n, y_n )$ von der Regressionsgeraden $R_{Y \to X}$ in $y$–Richtung ist minimal:
- $${\rm MQA}_Y = {\rm E} \big [ y_n - C_{Y \to X} \cdot x_n\big ]^2 = \frac{\rm 1}{N} \cdot \sum_{n=\rm 1}^{N}\; \;\big [y_n - C_{Y \to X} \cdot x_n\big ]^{\rm 2}={\rm Minimum}.$$
- Die zweite Gleichung gilt nur, wenn alle Punkte $(x_n, y_n )$ der 2D–WDF gleichwahrscheinlich sind.
$\text{(b)}\hspace{0.5cm} \text{Regressionsgerade }R_{X \to Y}$ (blaue Gerade in der App)
Die Regression in Gegenrichtung $($also von $X$ auf $Y)$ bedeutet dagegen, dass der $x$–Wert auf den $y$–Wert zurückgeführt wird. Für ${\rm MQA}_Y$ ergibt sich der minimale Wert.
- Geradengleichung, Winkel $\theta_{X \to Y}$ der Geraden $R_{X \to Y}$ zur $x$–Achse:
- $$y=C_{X \to Y} \cdot x \ \ \text{mit} \ \ C_{X \to Y}=\frac{\sigma_X}{\sigma_Y}\cdot\rho_{XY}= \frac{\mu_{XY}}{\sigma_Y^2},\hspace{0.6cm} \theta_{X \to Y}={\rm arctan}\ (C_{X \to Y}).$$
- Kriterium: Der mittlere Abstand aller Punkte $(x_n, y_n )$ von der Regressionsgeraden $R_{X \to Y}$ in $x$–Richtung ist minimal:
- $${\rm MQA}_X = {\rm E} \big [ x_n - y_n/C_{x \to y}\big ]^2 = \frac{\rm 1}{N} \cdot \sum_{n=\rm 1}^{N}\; \;\big [x_n - y_n/C_{x \to y}\big ]^{\rm 2}={\rm Minimum}.$$
$\text{Beispiel 2:}$ Es gelten die gleichen Voraussetzungen wie im $\text{Beispiel 1}$ und es werden teilweise auch die dort gefundenen Ergebnisse verwendet.
In der oberen Grafik ist die Regressionsgerade $R_{x \to y}$ als blaue Kurve eingezeichnet:
- Hierfür ergibt sich $C_{X \to Y}=\mu_{XY}/{\sigma_Y^2} = 1$ und dementsprechend $ \theta_{X \to Y}={\rm arctan}\ (1) = 45^\circ.$
- Für den mittleren Abstand aller vier Punkte $(x_n, y_n )$ von der Regressionsgeraden $R_{X \to Y}$ in $x$–Richtung erhält man unter Ausnutzung der Symmetrie (beachten Sie die eingezeichneten blauen Horizontalen):
- $${\rm MQA}_X = {\rm E} \big [ x_n - y_n/C_{x \to y}\big ]^2 = 2 \cdot \big [ 0.2 \cdot \left [1 - 1/1\right ]^{\rm 2} +0.3 \cdot \left [0.5 - 0/1\right ]^{\rm 2}\big ]=0.15.$$
- Jede Gerade mit einem anderen Winkel als $45^\circ$ führt hier zu einem größeren ${\rm MQA}_X$.
Betrachten wir nun die rote Regressionsgerade $R_{Y \to X}$ in der unteren Grafik.
- Hierfür ergibt sich $C_{Y \to X}=\mu_{XY}/{\sigma_X^2} = 0.4/0.55\approx0.727$ und $ \theta_{Y \to X}={\rm arctan}\ (0.727) \approx 36^\circ.$
- Hier ist nun der mittlere Abstand der vier Punkte $(x_n, y_n )$ von der Regressionsgeraden $R_{Y \to X}$ in $y$–Richtung minimal (beachten Sie die eingezeichneten roten Vertikalen):
- $${\rm MQA}_Y = {\rm E} \big [ y_n - C_{y \to x} \cdot x_n\big ]^2 = 2 \cdot \big [ 0.2 \cdot \left [1 - 0.727 \cdot 1\right ]^{\rm 2} +0.3 \cdot \left [0 - 0.727 \cdot 0.5 \right ]^{\rm 2}\big ]\approx 0.109.$$
Die im Text erwähnte „Korrelationsgerade” mit der Eigenschaft, dass der mittlere quadratische Euklidische Abstand $\rm (MQA)$ aller Punkte von dieser Geraden minimal ist, wird sicher zwischen den beiden hier berechneten Regressionsgeraden liegen.
Testbereich
Bitte überprüfen
- Hier habe ich als Test neben der roten und der blauen Geraden noch die grüne Gerade $H$ mit Winkel $\arctan(\rho) = \arctan(0.853)\approx 40^\circ$ eingezeichnet.
- Sollte das die Korrelationsgerade $K$ sein, dann müsste der mittlere quadratische (Euklidische) Abstand $\rm (MQA)$ aller Punkte von dieser Geraden minimal sein.
- Müsste dann für diese Gerade ${\rm MQA}={\rm MQA}_X + {\rm MQA}_Y$ minimal sein?
- Bitte für mehrere Parametersätze überprüfen. Ich hoffe, dass das nicht allgemein stimmt.
Bitte recherchieren. Das kann man mit dem Programm nicht überprüfen
- Könnte das wenigstens bei Gaußschen 2D–Zufallsgrößen gelten
- Durch die Tangenten sind die Regressionsgeraden bestimmt.
- Im anderen LNTwww und im Carolin-Programm bezeichnen wir die schwarze Gerade als Ellipsenhauptache und die rote Gerade als Korrelationsgerade.
- Wenn das stimmt, müsste ich das ändern. Die Änderungen im Programm selbst wären minimal.
Der Sonderfall Gaußscher 2D–Zufallsgrößen
Fehlt noch.
Versuchsdurchführung
Eventuell noch überarbeiten
- Wählen Sie zunächst die Nummer 1 ... 6 der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Hide solution”.
- Aufgabenstellung und Lösung in Englisch.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
Ende Überarbeitung Voreinstellung für Nummer 0 wie bei den Beispielen vorne
In den folgenden Aufgabenbeschreibungen werden folgende Kurzbezeichnungen verwendet:
- Rot: Regressionsgerade $R_{Y \to X}$ (im Applet rot gezeichnet),
- Blau: Regressionsgerade $R_{X \to Y}$ (im Applet blau gezeichnet).
(1) Mit welcher Parametereinstellung sind die beiden Regressionsgerade $R_{Y \to X}$ und $R_{X \to Y}$ deckungsgleich?
- Es ist offensichtlich, dass gleiche Regressionsgerade nur möglich sind, wenn diese unter dem Winkel $45^\circ$ verlaufen ⇒ „Winkelhalbierende”.
- Da die fest vorgegebenen Punkte $3$ und $4$ auf der Winkelhalbierenden liegen, muss dies auch für die Punkte $1$ und $2$ gelten ⇒ $y_1 = x_1$.
- Dies gilt für alle Parametereinstellungen $y_1 = x_1$ und auch für alle $p_1$ im erlaubten Bereich von $0$ bis $0.5$.
(2) Nun gelte $x_1 = 0.5,\ y_1 = 0,\ p_1 = 0.3$ Interpretieren Sie die Ergebnisse. Aktivieren Sie hierzu die Hilfsgerade.
- Diese Einstellung stimmt mit den Voraussetzungen von $\text{Beispiel 1}$ und $\text{Beispiel 2}$ überein. Insbesondere gilt $ \theta_{X \to Y}= 45^\circ.$ und $ \theta_{Y \to X}\approx 36^\circ$.
- Durch Variation des Winkels $ \theta_{\rm H}$ erkennt man, dass tatsächlich für $ \theta_{\rm H}= 45^\circ$ die Kenngröße ${\rm MQA}_X =0.15$ den kleinsmöglichen Wert annimmt.
- Ebenso ergibt sich der kleinsmöglicher Abstand ${\rm MQA}_Y =0.109$ in $y$–Richtung für $ \theta_{\rm H}= 36^\circ$, also entsprechend der Regressionsgeraden $R_{y \to x}$.
(3) Es gelten zunächst weiter die Einstellungen von (2). Wie ändern sich die Ergebnisse nach Variation des Parameters $p_1$ im erlaubten Bereich $(0\le p_1 \le 0.5)$?
- Die blaue Regressionsgerade verläuft weiter unter dem Winkel $ \theta_{X \to Y}= 45^\circ$. Das heißt: es gilt hier $\mu_{XY} =\sigma_Y^2$, und zwar unabhängig von $p_1 < 0.5$.
- Im Grenzfall $p_1 = 0.5$ ist wegen $\sigma_Y =0$ die blaue Regressionsgerade undefiniert. Es handelt sich nurmehr um eine 1D–Zufallsgröße $X$.
- Mit $p_1=0$ sind nur die äußeren Punkte $3$ und $4$ wirksam ⇒ $ \theta_{Y \to X}= \theta_{X \to Y}= 45^\circ$, mit $p_1=0.5$ nur die inneren Punkte $1$ und $2$ ⇒ $ \theta_{Y \to X}= 0^\circ$.
- Dazwischen wird die rote Regressionsgerade kontinuierlich flacher. Sind alle Punkte gleichwahrscheinlich $(p_1=0.25)$, dann ist $\theta_{Y \to X}\approx 38.7^\circ$.
(4) Nun gelte $x_1 = 0,\ y_1 = 0.5,\ p_1 = 0.3$. Variieren Sie $p_1$ im Bereich $0\le p_1 < 0.5$ und interpretieren Sie die Ergebnisse. $(p_1 = 0.5)$ sollte man ausschließen.
- Wegen $\sigma_X \le \sigma_Y$ liegt weiterhin die blaue Gerade nie unterhalb der roten, die nun für alle $p_1 \ne 0.5$ die Winkelhalbierende ist ⇒ $ \theta_{Y \to X}\approx 45^\circ$.
- Der Winkel der blauen Regressionsgerade wächst von $ \theta_{X \to Y}= 45^\circ \ (p_1 = 0)$ bis $ \theta_{X \to Y} \to 45^\circ \ (p_1 \to 0.5)$ kontinuierlich an.
(5) Beginnen Sie mit $x_1 = 0.8,\ y_1 = -0.8,\ p_1 = 0.25$ vergrößern Sie $y_1$ bis zum Endwert $y_1 = +0.8$. Interpretieren Sie die Ergebnisse.
- Für $y_1 =-0.8$ ist $ \theta_{X \to Y}= 77.6^\circ$ und $ \theta_{Y \to X}= 12.4^\circ$. Mit steigendem $y_1$ verläuft die blaue Gerade $ R_{X \to Y}$ flacher und die rote $ (R_{Y \to X})$ steiler.
- Im Endpunkt $(y_1 = +0.8)$ verlaufen die beiden Regressionsgeraden deckungsgleich unter dem Winkel $ \theta_{X \to Y}= \theta_{Y \to X}= 45^\circ$.
(6) Abschließend gelte $x_1 = +1,\ y_1 = -1$. Variieren Sie $p_1$ im gesamten zulässigen Bereich $0\le p_1 \le 0.5$. Wann sind die beiden Zufallsgrößen unkorreliert?
- Für $p_1 = 0$ gilt $ \theta_{X \to Y}=\theta_{Y \to X}= 45^\circ.$ Anschließend dreht die blaue Gerade entgegen dem Uhrzeigersinn und die rote Gerade im Uhrzeigersinn.
- Für $p_1 = 0.25$ sind die Winkel $ \theta_{X \to Y}=90^\circ, \ \theta_{Y \to X}= 0^\circ.$ Diese Momentaufnahme trifft genau den Fall unkorrelierter Zufallsgrößen ⇒ $\mu_{XY}=0$.
- Anschließend drehen beide Geraden weiter in gleicher Richtung. Für $p_1 = 0.5$ gilt schließlich: $ \theta_{X \to Y}=135^\circ= -45^\circ, \ \theta_{Y \to X}= -45^\circ.$
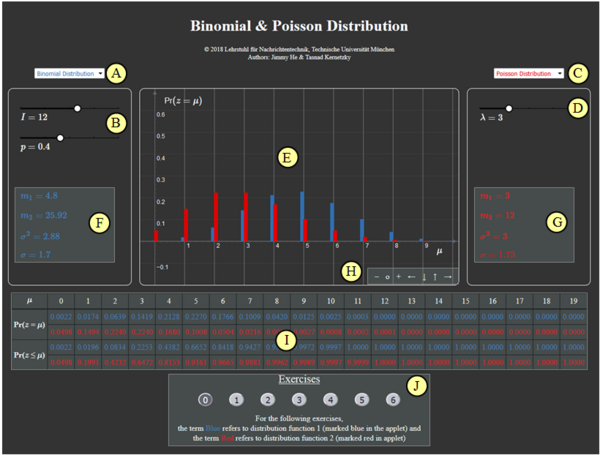
Zur Handhabung des Applets
(A) Vorauswahl für blauen Parametersatz
(B) Parametereingabe $I$ und $p$ per Slider
(C) Vorauswahl für roten Parametersatz
(D) Parametereingabe $\lambda$ per Slider
(E) Graphische Darstellung der Verteilungen
(F) Momentenausgabe für blauen Parametersatz
(G) Momentenausgabe für roten Parametersatz
(H) Variation der grafischen Darstellung
$\hspace{1.5cm}$„$+$” (Vergrößern),
$\hspace{1.5cm}$ „$-$” (Verkleinern)
$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.
( I ) Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$
(J) Bereich für die Versuchsdurchführung
Andere Möglichkeiten zur Variation der grafischen Darstellung:
- Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
- Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde das Programm von Jimmy He (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.