Applets:Kohärentes und inkohärentes On-Off-Keying: Unterschied zwischen den Versionen
| Zeile 26: | Zeile 26: | ||
[[Datei:P ID2054 Dig T 4 4 S3 version1.png|right|frame|Signalraumkonstellationen für On–Off–Keying|class=fit]] | [[Datei:P ID2054 Dig T 4 4 S3 version1.png|right|frame|Signalraumkonstellationen für On–Off–Keying|class=fit]] | ||
| − | $\rm OOK$ ist ein eindimensionales Modulationsverfahren mit $s_{1} \equiv 0$ und | + | $\rm OOK$ ist ein binäres und eindimensionales Modulationsverfahren mit $s_{1} \equiv 0$ und |
| − | *$s_{0} = \{E^{1/2}, 0\}$ (bei Cosinus–Träger) bzw. | + | *$s_{0} = \{E^{1/2}, 0\}$ (bei Cosinus–Träger, linke Grafik) bzw. |
| − | *$s_{0} = \{0, -E^{1/2}\}$ (bei Sinus–Träger). | + | *$s_{0} = \{0, -E^{1/2}\}$ (bei Sinus–Träger, rechte Grafik). |
| − | Bei kohärenter Demodulation ist die Signalraumkonstellation des Empfangssignals gleich der des Sendesignals und besteht wieder aus den zwei Punkten $\boldsymbol{r}_0=\boldsymbol{s}_0$ und $\boldsymbol{r}_1=\boldsymbol{s}_1$. | + | Bei kohärenter Demodulation ist die Signalraumkonstellation des Empfangssignals gleich der des Sendesignals und besteht wieder aus den zwei Punkten $\boldsymbol{r}_0=\boldsymbol{s}_0$ und $\boldsymbol{r}_1=\boldsymbol{s}_1$. In diesem Fall ist das AWGN–Rauschen eindimensional mit der Varianz $\sigma^2 = N_0/2$ anzusetzen und man erhält entsprechend dem [[Digitalsignalübertragung/Approximation_der_Fehlerwahrscheinlichkeit#Fehlerwahrscheinlichkeit_bei_gleichwahrscheinlichen_Symbolen| Theorieteil]] für die '''Bitfehlerwahrscheinlichkeit''' $p_{\rm B} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s})$: |
| − | + | :$$p_{\rm B} = {\rm Q} \left ( \frac{\sqrt{E}/2}{\sigma}\right ) = {\rm Q} \left ( \sqrt{\frac{E}{2 N_0}}\right ) | |
| − | |||
| − | :$$p_{\rm B} = {\rm Q} \left ( \frac{ | ||
= {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.$$ | = {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.$$ | ||
| − | *Diese Gleichung gilt für gleichwahrscheinliche Symbole | + | *Diese Gleichung gilt für gleichwahrscheinliche Symbole mit der Entscheiderschwelle $G$ in der Mitte zwischen $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$.<br> |
*$E_{\rm B}=E/2$ bezeichnet für diesen Fall die „mittlere Energie pro Bit” und $N_0$ die (einseitige) AWGN–Rauschleistungsdichte. | *$E_{\rm B}=E/2$ bezeichnet für diesen Fall die „mittlere Energie pro Bit” und $N_0$ die (einseitige) AWGN–Rauschleistungsdichte. | ||
*Die Funktion ${\rm Q}(x)$ nennt man das „Komplementäre Gaußsche Fehlerintegral”. Der Link weist auf das Applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|Komplementäre Gaußsche Fehlerfunktionen]]. | *Die Funktion ${\rm Q}(x)$ nennt man das „Komplementäre Gaußsche Fehlerintegral”. Der Link weist auf das Applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|Komplementäre Gaußsche Fehlerfunktionen]]. | ||
| + | |||
| + | |||
| + | [[Datei:P ID3148 Dig T 4 5 S2c version1.png|right|frame|Dichtefunktionen für „OOK, nichtkohärent”]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Die Grafik zeigt das Ergebnis dieser Gleichung für $\sigma_n = 0.5$ und $C = 2$, wobei die (rote) Rice–WDF durch eine Gauß–WDF mit Mittelwert $C$ und Streuung $\sigma_n$ approximiert ist. Man erkennt daraus: | ||
| + | *Die optimale Entscheidungsgrenze $($hier: $G \approx 1.25)$ ergibt sich aus dem Schnittpunkt der beiden Kurven.<br> | ||
| + | *Die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ist die Summe der beiden farblich hinterlegten Flächen. Im Beispiel ergibt sich $p_{\rm S} \approx 5\%$. | ||
| + | |||
| + | |||
| + | Die Fehlerwahrscheinlichkeit für andere Werte von $C$ und $\sigma_n$ sowie die optimale Entscheidungsgrenze $G$ können Sie mit dem Berechnungstool [[Applets:On-Off-Keying|Nichtkohärentes On–Off–Keying]] bestimmen.}} | ||
===On–Off–Keying mit inkohärenter Demodulation=== | ===On–Off–Keying mit inkohärenter Demodulation=== | ||
| − | Die | + | Die folgende Grafik zeigt die Strukur (im äquivalenten Tiefpassbereich) des optimalen OOK–Empfängers für inkohärente Demodulation. [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Nichtkoh.C3.A4rente_Demodulation_von_On.E2.80.93Off.E2.80.93Keying|Detailbeschreibung]] |
[[Datei:P ID3147 Dig T 4 5 S2b version1.png|right|frame|Empfänger für inkohärente OOK-Demodulation (komplexe Signale sind blau beschriftet)|class=fit]] | [[Datei:P ID3147 Dig T 4 5 S2b version1.png|right|frame|Empfänger für inkohärente OOK-Demodulation (komplexe Signale sind blau beschriftet)|class=fit]] | ||
| Zeile 54: | Zeile 62: | ||
*Ist der Entscheidungswert $y \gt G$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$. | *Ist der Entscheidungswert $y \gt G$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$. | ||
| − | *Somit | + | *Somit ist die mittlere Bitfehlerwahrscheinlichkeit als Summe zweier Verbundwahrscheinlichkeiten darstellbar: |
| − | :$$p_{\rm B} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = | + | :$$p_{\rm B} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) |
| − | + | + | + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}).$$ |
===Fehlerwahrscheinlichkeitsberechnung unter Berücksichtigung von Rayleigh– und Riceverteilung=== | ===Fehlerwahrscheinlichkeitsberechnung unter Berücksichtigung von Rayleigh– und Riceverteilung=== | ||
| − | Zur Berechnung der Bitfehlerwahrscheinlichkeit bei inkohärenter Demodulation gehen wir von der rechten Skizze der nachfolgenden Grafik aus. Dargestellt ist das Empfangssignal im äquivalenten Tiefpassbereich in der komplexen Ebene. | + | Zur Berechnung der Bitfehlerwahrscheinlichkeit bei inkohärenter Demodulation gehen wir von der rechten Skizze der nachfolgenden Grafik aus. Dargestellt ist das Empfangssignal im äquivalenten Tiefpassbereich in der komplexen Ebene. |
[[Datei:P ID2083 Dig T 4 5 S2a version1.png|right|frame|??? Kohärente und Inkohärente Demodulation von On-Off-Keying|class=fit]] | [[Datei:P ID2083 Dig T 4 5 S2a version1.png|right|frame|??? Kohärente und Inkohärente Demodulation von On-Off-Keying|class=fit]] | ||
| − | *Der Punkt $\boldsymbol{s_1}=0$ führt im Empfangsignal zu $\boldsymbol{r_1}=0$. | + | *Der Punkt $\boldsymbol{s_1}=0$ führt im Empfangsignal wieder zu $\boldsymbol{r_1}=0$. |
| − | *Dagegen wird aus dem Punkt $\boldsymbol{s_0}=1$ wegen des Phasenwinkels $\phi$ der Kreis $\boldsymbol{ | + | *Dagegen wird aus dem Punkt $\boldsymbol{s_0}=1$ wegen des gleichverteilten Phasenwinkels $\phi$ der Kreis $\boldsymbol{r_0}$ mit Radius $1$. |
| − | *Die Entscheidungsregion für die $1$ ist ebenfalls kreisförmig mit Radius $G$. | + | *Die Entscheidungsregion für die $1$ ist ebenfalls kreisförmig mit Radius $G$. Der richtige Wert ist noch zu bestimmen. |
| − | *Unter Berücksichtigung des AWGN–Rauschens gilt dann $\boldsymbol{r_1}=\boldsymbol{s_1} + \boldsymbol{n_1}$. Die Rauschkomponente $\boldsymbol{n_1}$ besitzt eine [[Stochastische_Signaltheorie/Weitere_Verteilungen#Rayleighverteilung|Rayleighverteilung]] $($Betrag der beiden mittelwertfreien Gaußkomponenten für $\rm I$ und $\rm Q)$. Damit erhält man | + | *Unter Berücksichtigung des AWGN–Rauschens gilt dann $\boldsymbol{r_1}=\boldsymbol{s_1} + \boldsymbol{n_1}$. |
| + | *Die Rauschkomponente $\boldsymbol{n_1}$ besitzt eine [[Stochastische_Signaltheorie/Weitere_Verteilungen#Rayleighverteilung|Rayleighverteilung]] $($Betrag der beiden mittelwertfreien Gaußkomponenten für $\rm I$ und $\rm Q)$. Diese lautet mit der rotationssymmetrischen Rauschkomponente $\eta$: | ||
| + | :$$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1})=\frac{\eta}{\sigma^2}\cdot {\rm e}^{-\eta^2 / ( 2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma^2) } .$$ | ||
| + | *Damit erhält man für die bedingte Wahrscheinlichkeit | ||
:$${\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1}) = \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1}) \,{\rm d} \eta | :$${\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1}) = \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1}) \,{\rm d} \eta | ||
| + | \hspace{0.05cm},$$ | ||
| + | :und mit dem Faktor $1/2$ (gleichwahrscheinliche Sendesymbole) die Verbundwahrscheinlichkeit: | ||
| + | :$${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) = 1/2 \cdot {\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1})= 1/2 \cdot \int_{G}^{\infty}p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1}) \,{\rm d} \eta | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Die Rauschkomponente $\boldsymbol{n_0}$ besitzt eine [[Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung|Riceverteilung]] $($Betrag der Gaußkomponenten mit Mittelwerten $m_x$ und $m_y)$ ⇒ Konstante $C=\sqrt{m_x^2 + m_y^2}$: |
| − | :$$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{ | + | |
| + | :$$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0})=\frac{\eta}{\sigma^2}\cdot{\rm e}^{-({C^2+\it \eta^{\rm 2} })/ ({\rm 2 \it \sigma^{\rm 2} })}\cdot {\rm I_0}(\frac{\it \eta\cdot C}{\sigma^{\rm 2} }) \hspace{0.4cm}{\rm mit} \hspace{0.4cm} {\rm I_0}(\eta) = \sum_{k=0}^{\infty}\frac{(\eta/2)^{2k} }{k! \cdot {\rm \Gamma ({\it k}+1)} }.$$ | ||
| + | *Damit ergibt sich für die zweite Verbundwahrscheinlichkeit: | ||
| + | |||
| + | :$${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) = 1/2 \cdot \int_{0}^{G}p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0}) \,{\rm d} \eta | ||
| + | \hspace{0.05cm}.$$ | ||
| + | === Vorerst ENDE=== | ||
*Analog dazu gilt für die zweite bedingte Wahrscheinlichkeit in obiger Gleichung: | *Analog dazu gilt für die zweite bedingte Wahrscheinlichkeit in obiger Gleichung: | ||
:$${\rm Pr}(\boldsymbol{r_1}|\boldsymbol{s_0}) = \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0}) \,{\rm d} \eta | :$${\rm Pr}(\boldsymbol{r_1}|\boldsymbol{s_0}) = \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0}) \,{\rm d} \eta | ||
\hspace{0.05cm},\hspace{0.3cm}\text{mit}$$ | \hspace{0.05cm},\hspace{0.3cm}\text{mit}$$ | ||
| − | + | ||
Wir betrachten [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#On.E2.80.93Off.E2.80.93Keying_.282.E2.80.93ASK.29|On–Off–Keying]] (bzw. 2–ASK) im äquivalenten Tiefpassbereich. | Wir betrachten [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#On.E2.80.93Off.E2.80.93Keying_.282.E2.80.93ASK.29|On–Off–Keying]] (bzw. 2–ASK) im äquivalenten Tiefpassbereich. | ||
Version vom 28. November 2020, 17:33 Uhr
Applet in neuem Tab öffnen English Version
Inhaltsverzeichnis
Programmbeschreibung
Dargestellt werden impulsförmige symmetrische Zeitsignale ⇒ „Impulse” $x(t)$ und die dazugehörigen Spektralfunktionen $X(f)$, nämlich
- Gaußimpuls (englisch: Gaussian pulse),
- Rechteckimpuls (englisch: Rectangular pulse),
- Dreieckimpuls (englisch: Triangular pulse),
- Trapezimpuls (englisch: Trapezoidal pulse),
- Cosinus–Rolloff–Impuls (englisch: Cosine-rolloff pulse).
Weiter ist zu beachten:
- Die Funktionen $x(t)$ bzw. $X(f)$ werden für bis zu zwei Parametersätzen in jeweils einem Diagramm dargestellt.
- Die roten Kurven und Zahlenangaben gelten für den linken Parametersatz, die blauen für den rechten Parametersatz.
- Die Abszissen $t$ (Zeit) und $f$ (Frequenz) sowie die Ordinaten $x(t)$ (Signalwerte) bzw. $X(f)$ (Spektralwerte) sind jeweils normiert.
Theoretischer Hintergrund
On–Off–Keying mit kohärenter Demodulation
Das einfachste digitale Modulationsverfahren ist On–Off–Keying $\rm (OOK)$. Dieses Verfahren wird teilweise auch als Amplitude Shift Keying $\rm (2–ASK)$ bezeichnet und kann im äquivalenten Tiefpassbereich wie folgt charakterisiert werden:
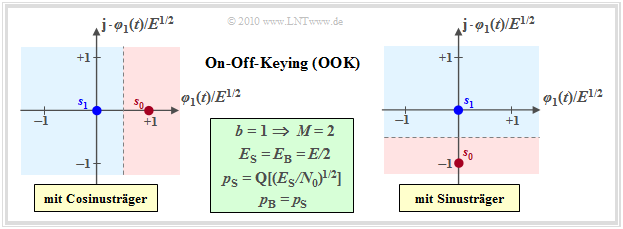
$\rm OOK$ ist ein binäres und eindimensionales Modulationsverfahren mit $s_{1} \equiv 0$ und
- $s_{0} = \{E^{1/2}, 0\}$ (bei Cosinus–Träger, linke Grafik) bzw.
- $s_{0} = \{0, -E^{1/2}\}$ (bei Sinus–Träger, rechte Grafik).
Bei kohärenter Demodulation ist die Signalraumkonstellation des Empfangssignals gleich der des Sendesignals und besteht wieder aus den zwei Punkten $\boldsymbol{r}_0=\boldsymbol{s}_0$ und $\boldsymbol{r}_1=\boldsymbol{s}_1$. In diesem Fall ist das AWGN–Rauschen eindimensional mit der Varianz $\sigma^2 = N_0/2$ anzusetzen und man erhält entsprechend dem Theorieteil für die Bitfehlerwahrscheinlichkeit $p_{\rm B} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s})$:
- $$p_{\rm B} = {\rm Q} \left ( \frac{\sqrt{E}/2}{\sigma}\right ) = {\rm Q} \left ( \sqrt{\frac{E}{2 N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.$$
- Diese Gleichung gilt für gleichwahrscheinliche Symbole mit der Entscheiderschwelle $G$ in der Mitte zwischen $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$.
- $E_{\rm B}=E/2$ bezeichnet für diesen Fall die „mittlere Energie pro Bit” und $N_0$ die (einseitige) AWGN–Rauschleistungsdichte.
- Die Funktion ${\rm Q}(x)$ nennt man das „Komplementäre Gaußsche Fehlerintegral”. Der Link weist auf das Applet Komplementäre Gaußsche Fehlerfunktionen.
$\text{Beispiel 1:}$ Die Grafik zeigt das Ergebnis dieser Gleichung für $\sigma_n = 0.5$ und $C = 2$, wobei die (rote) Rice–WDF durch eine Gauß–WDF mit Mittelwert $C$ und Streuung $\sigma_n$ approximiert ist. Man erkennt daraus:
- Die optimale Entscheidungsgrenze $($hier: $G \approx 1.25)$ ergibt sich aus dem Schnittpunkt der beiden Kurven.
- Die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ist die Summe der beiden farblich hinterlegten Flächen. Im Beispiel ergibt sich $p_{\rm S} \approx 5\%$.
Die Fehlerwahrscheinlichkeit für andere Werte von $C$ und $\sigma_n$ sowie die optimale Entscheidungsgrenze $G$ können Sie mit dem Berechnungstool Nichtkohärentes On–Off–Keying bestimmen.
On–Off–Keying mit inkohärenter Demodulation
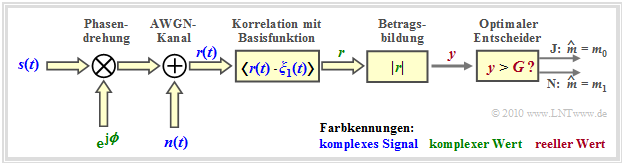
Die folgende Grafik zeigt die Strukur (im äquivalenten Tiefpassbereich) des optimalen OOK–Empfängers für inkohärente Demodulation. Detailbeschreibung
Entsprechend dieser zweiten Grafik gilt:
- Das Eingangssignal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ ist aufgrund des Phasenwinkels $\phi$ und wegen des komplexen Rauschterms $\boldsymbol{n}(t)$ im allgemeinen komplex.
- Erforderlich ist nun die Korrelation zwischen dem komplexen Empfangssignal $\boldsymbol{r}(t)$ und einer komplexen Basisfunktion $\boldsymbol{\xi}(t)$.
- Das Ergebnis ist der (komplexe) Detektorwert $\boldsymbol{r}$, woraus als reelle Entscheidereingangsgröße der Betrag $y = |\boldsymbol{r}(t)|$ gebildet wird.
- Ist der Entscheidungswert $y \gt G$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$.
- Somit ist die mittlere Bitfehlerwahrscheinlichkeit als Summe zweier Verbundwahrscheinlichkeiten darstellbar:
- $$p_{\rm B} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}).$$
Fehlerwahrscheinlichkeitsberechnung unter Berücksichtigung von Rayleigh– und Riceverteilung
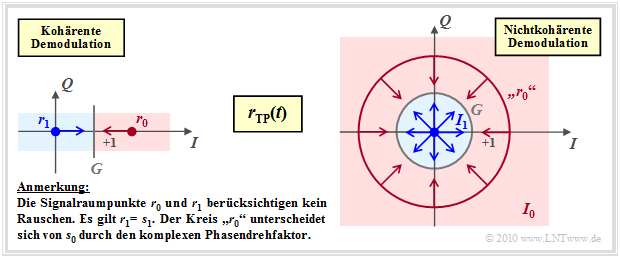
Zur Berechnung der Bitfehlerwahrscheinlichkeit bei inkohärenter Demodulation gehen wir von der rechten Skizze der nachfolgenden Grafik aus. Dargestellt ist das Empfangssignal im äquivalenten Tiefpassbereich in der komplexen Ebene.
- Der Punkt $\boldsymbol{s_1}=0$ führt im Empfangsignal wieder zu $\boldsymbol{r_1}=0$.
- Dagegen wird aus dem Punkt $\boldsymbol{s_0}=1$ wegen des gleichverteilten Phasenwinkels $\phi$ der Kreis $\boldsymbol{r_0}$ mit Radius $1$.
- Die Entscheidungsregion für die $1$ ist ebenfalls kreisförmig mit Radius $G$. Der richtige Wert ist noch zu bestimmen.
- Unter Berücksichtigung des AWGN–Rauschens gilt dann $\boldsymbol{r_1}=\boldsymbol{s_1} + \boldsymbol{n_1}$.
- Die Rauschkomponente $\boldsymbol{n_1}$ besitzt eine Rayleighverteilung $($Betrag der beiden mittelwertfreien Gaußkomponenten für $\rm I$ und $\rm Q)$. Diese lautet mit der rotationssymmetrischen Rauschkomponente $\eta$:
- $$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1})=\frac{\eta}{\sigma^2}\cdot {\rm e}^{-\eta^2 / ( 2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma^2) } .$$
- Damit erhält man für die bedingte Wahrscheinlichkeit
- $${\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1}) = \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1}) \,{\rm d} \eta \hspace{0.05cm},$$
- und mit dem Faktor $1/2$ (gleichwahrscheinliche Sendesymbole) die Verbundwahrscheinlichkeit:
- $${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) = 1/2 \cdot {\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1})= 1/2 \cdot \int_{G}^{\infty}p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1}) \,{\rm d} \eta \hspace{0.05cm}.$$
- Die Rauschkomponente $\boldsymbol{n_0}$ besitzt eine Riceverteilung $($Betrag der Gaußkomponenten mit Mittelwerten $m_x$ und $m_y)$ ⇒ Konstante $C=\sqrt{m_x^2 + m_y^2}$:
- $$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0})=\frac{\eta}{\sigma^2}\cdot{\rm e}^{-({C^2+\it \eta^{\rm 2} })/ ({\rm 2 \it \sigma^{\rm 2} })}\cdot {\rm I_0}(\frac{\it \eta\cdot C}{\sigma^{\rm 2} }) \hspace{0.4cm}{\rm mit} \hspace{0.4cm} {\rm I_0}(\eta) = \sum_{k=0}^{\infty}\frac{(\eta/2)^{2k} }{k! \cdot {\rm \Gamma ({\it k}+1)} }.$$
- Damit ergibt sich für die zweite Verbundwahrscheinlichkeit:
- $${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) = 1/2 \cdot \int_{0}^{G}p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0}) \,{\rm d} \eta \hspace{0.05cm}.$$
Vorerst ENDE
- Analog dazu gilt für die zweite bedingte Wahrscheinlichkeit in obiger Gleichung:
- $${\rm Pr}(\boldsymbol{r_1}|\boldsymbol{s_0}) = \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0}) \,{\rm d} \eta \hspace{0.05cm},\hspace{0.3cm}\text{mit}$$
Wir betrachten On–Off–Keying (bzw. 2–ASK) im äquivalenten Tiefpassbereich.
- Bei kohärenter Demodulation (linke Grafik) ist die Signalraumkonstellation des Empfangssignals gleich der des Sendesignals und besteht aus zwei Punkten.
- Die Entscheidungsgrenze $G$ liegt in der Mitte zwischen diesen Punkten $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$.
- Die Pfeile markieren die grobe Richtung von Rauschvektoren, die eventuell zu Übertragungsfehlern führen.
Dagegen gilt bei nichtkohärenter Demodulation (rechte Grafik):
- Der Punkt $\boldsymbol{r}_1 = \boldsymbol{s}_1 = 0$ bleibt weiter erhalten. Dagegen kann $\boldsymbol{r}_0 = \boldsymbol{s}_0 \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi}$ auf jeden Punkt des Kreises um $\boldsymbol{s}_0$ liegen, da $\phi$ unbekannt ist.
- Der Entscheidungsprozess unter Berücksichtigung des AWGN–Rauschens ist nun zweidimensional zu interpretieren, wie durch die Pfeile in der rechten Grafik angedeutet.
- Das Entscheidungsgebiet $I_1$ ist ein Kreis, dessen Radius $G$ ein optimierbarer Parameter ist. Das Entscheidungsgebiet $I_0$ liegt außerhalb des Kreises.
Damit liegt die Strukur des optimalen OOK–Empfängers (im äquivalenten Tiefpassbereich) fest. Entsprechend dieser zweiten Grafik gilt:
- Das Eingangssignal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ ist aufgrund des Phasenwinkels $\phi$ und wegen des komplexen Rauschterms $\boldsymbol{n}(t)$ im allgemeinen komplex. Erforderlich ist demzufolge nun die Korrelation zwischen dem komplexen Empfangssignal $\boldsymbol{r}(t)$ und einer komplexen Basisfunktion $\boldsymbol{\xi}_1(t)$.
- Das Ergebnis ist der (komplexe) Detektorwert $\boldsymbol{r}$, woraus als reelle Entscheidereingangsgröße der Betrag $y = |\boldsymbol{r}(t)|$ gebildet wird.
- Ist der Entscheidungswert $y \gt G$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$. Somit beträgt die Fehlerwahrscheinlichkeit bei gleichwahrscheinlichen Symbolen:
- \[p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}|\hspace{0.05cm} m_0) \,{\rm d} \eta + {1}/{ 2} \cdot \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} m_1) \,{\rm d} \eta \hspace{0.05cm}.\]
- Aufgrund der Rice–WDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_0)$ und der Rayleigh–WDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_1)$ kann allerdings diese Wahrscheinlichkeit nur numerisch ermittelt werden. Die optimale Entscheidungsgrenze $G$ ist vorher als die Lösung der folgenden Gleichung zu bestimmen:
- \[p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_0) = p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_1) \hspace{0.05cm}.\]
$\text{Beispiel 1:}$ Die Grafik zeigt das Ergebnis dieser Gleichung für $\sigma_n = 0.5$ und $C = 2$, wobei die (rote) Rice–WDF durch eine Gauß–WDF mit Mittelwert $C$ und Streuung $\sigma_n$ approximiert ist. Man erkennt daraus:
- Die optimale Entscheidungsgrenze $($hier: $G \approx 1.25)$ ergibt sich aus dem Schnittpunkt der beiden Kurven.
- Die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ist die Summe der beiden farblich hinterlegten Flächen. Im Beispiel ergibt sich $p_{\rm S} \approx 5\%$.
Die Fehlerwahrscheinlichkeit für andere Werte von $C$ und $\sigma_n$ sowie die optimale Entscheidungsgrenze $G$ können Sie mit dem Berechnungstool Nichtkohärentes On–Off–Keying bestimmen.
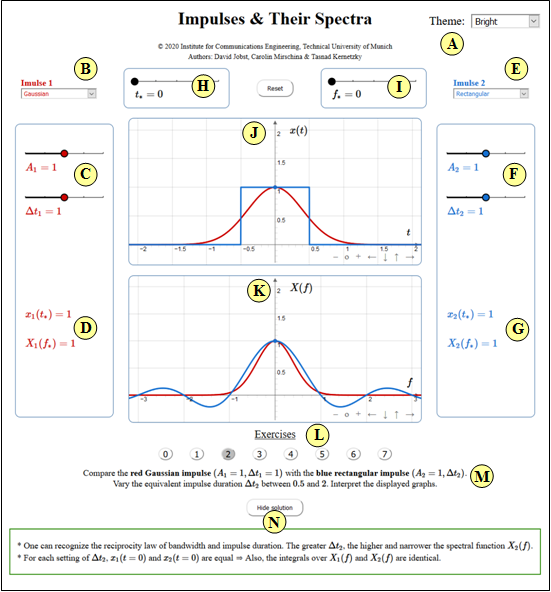
Versuchsdurchführung
- Wählen Sie zunächst die Nummer $(1,\ 2$, ... $)$ der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer $0$ entspricht einem „Reset”: Einstellung wie beim Programmstart.
- „Rot” bezieht sich auf den ersten Parametersatz ⇒ $x_1(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_1(f)$.
- „Blau” bezieht sich auf den zweiten Parametersatz ⇒ $x_2(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_2(f)$.
- Werte betragsmäßig kleiner $0.0005$ werden im Programm zu Null gesetzt.
(1) Vergleichen Sie den roten Gaußimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem blauen Rechteckimpuls $(A_2 = 1, \Delta t_2 = 1)$ ⇒ Voreinstellung.
Welche Unterschiede erkennt man im Zeit- und im Frequenzbereich?
- Der Gaußimpuls reicht sowohl im Zeit– als auch im Frequenzbereich theoretisch bis ins Unendliche.
- Praktisch sind aber $x_1(t)$ für $|t| > 1.5$ und $X_1(f)$ für $|f| > 1.5$ nahezu Null.
- Das Rechteck ist zeitlich steng begrenzt: $x_2(|t| > 0.5) \equiv 0$. $X_2(f)$ hat in einem viel größeren Bereich als $X_1(f)$ Anteile.
- Es gilt $X_1(f = 0) = X_2(f = 0)$, weil das Integral über den Gaußimpuls $x_1(t)$ gleich dem Integral über den Rechteckimpuls $x_2(t)$ ist.
(A) Theme (veränderbare grafische Oberflächengestaltung)
- Dark: schwarzer Hintergrund (wird von den Autoren empfohlen)
- Bright: weißer Hintergrund (empfohlen für Beamer und Ausdrucke)
- Deuteranopia: für Nutzer mit ausgeprägter Grün–Sehschwäche
- Protanopia: für Nutzer mit ausgeprägter Rot–Sehschwäche
(B) Vorauswahl für die Impulsform $x_1(t)$ (rote Kurve)
(C) Parameterfestlegung für $x_1(t)$
(D) Numerikausgabe für $x_1(t_*)$ und $X_1(f_*)$
(E) Vorauswahl für die Impulsform $x_2(t)$ (blaue Kurve)
(F) Parameterfestlegung für $x_2(t)$
(G) Numerikausgabe für $x_2(t_*)$ und $X_2(f_*)$
(H) Einstellung der Zeit $t_*$ für die Numerikausgabe
(I) Einstellung der Frequenz $f_*$ für die Numerikausgabe
(J) Bereich der graphischen Darstellung im Zeitbereich
(K) Bereich der graphischen Darstellung im Frequenzbereich
(L) Auswahl der Aufgabe entsprechend der Aufgabennummer
(M) Aufgabenbeschreibung und Fragestellung
(N) Musterlösung anzeigen und verbergen
Details zu den obigen Punkten (J ) und (K)
Zoom–Funktionen:
„$+$” (Vergrößern), „$-$” (Verkleinern), „$\rm o$” (Zurücksetzen)
Verschiebe–Funktionen: „$\leftarrow$” „$\uparrow$” „$\downarrow$” „$\rightarrow$”
„$\leftarrow$” bedeutet: Bildausschnitt nach links, Ordinate nach rechts
Andere Möglichkeiten:
- Bei gedrückter Shifttaste und Scrollen kann im Koordinatensystem gezoomt werden.
- Bei gedrückter Shifttaste und gedrückter linker Maustaste kann das Koordinatensystem verschoben werden.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder und Klaus Eichin).
- 2017 wurde „Impulse & Spektren” von David Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.
- Letztmalige Überarbeitung 2020 durch Carolin Mirschina im Rahmen einer Werkstudententätigkeit.