Aufgaben:Aufgabe 1.1Z: ISDN-Verbindung: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 59: | Zeile 59: | ||
*Die Nachrichtensinke ist der Anrufbeantworter. | *Die Nachrichtensinke ist der Anrufbeantworter. | ||
*Bei einem idealen Übertragungssystem müsste $v(t) = {q(t)}$ gelten. | *Bei einem idealen Übertragungssystem müsste $v(t) = {q(t)}$ gelten. | ||
| − | * Aufgrund des additiven Rauschterms ${n(t)}$, der Dämpfung $\alpha$ und der Laufzeit $\tau$ gilt jedoch hier: | + | * Aufgrund des additiven Rauschterms ${n(t)}$, der Dämpfung $\alpha$ und der Laufzeit $\tau$ gilt jedoch hier: |
:$$v(t) = \alpha \cdot q ( t - \tau) + n(t).$$ | :$$v(t) = \alpha \cdot q ( t - \tau) + n(t).$$ | ||
*Es handelt sich nach unseren Definitionen um ein verzerrungsfreies System. | *Es handelt sich nach unseren Definitionen um ein verzerrungsfreies System. | ||
Aktuelle Version vom 8. April 2021, 09:45 Uhr
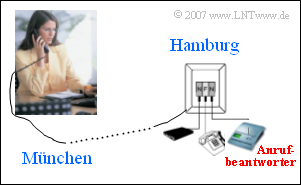
Wir betrachten das im Bild dargestellte Szenario:
Eine Münchnerin wählt mit ihrem ISDN-Telefon eine Rufnummer in Hamburg. Sie erreicht jedoch den gewünschten Gesprächspartner nicht, und hinterlässt ihm deshalb eine Nachricht auf Band.
Die verzerrungsfreie Verbindung wird durch
- einen Dämpfungsfaktor $\alpha$,
- eine Laufzeit $\tau$ und
- das momentane Signal-zu-Rauschverhältnis (SNR)
vollständig beschrieben.
Hinweis: Die Aufgabe soll einen Bezug zwischen diesem realen Szenario und den im Theorieteil genannten Funktionseinheiten eines allgemeinen Nachrichtenübertragungssystems herstellen.
Fragebogen
Musterlösung
(1) Die ersten beiden Aussagen sind richtig:
- Das Sprachsignal ${q(t)}$ muss zunächst in ein elektrisches Signal gewandelt und anschließend für die Übertragung aufbereitet werden.
- Bei ISDN ist das Sendesignal ${s(t)}$ digital.
(2) Richtig sind die Lösungsvorschläge 3 und 4:
- Das Empfangssignal ${r(t)}$ ist aufgrund des unvermeidbaren thermischen Rauschens stets analog.
- Die Nachrichtensinke ist der Anrufbeantworter.
- Bei einem idealen Übertragungssystem müsste $v(t) = {q(t)}$ gelten.
- Aufgrund des additiven Rauschterms ${n(t)}$, der Dämpfung $\alpha$ und der Laufzeit $\tau$ gilt jedoch hier:
- $$v(t) = \alpha \cdot q ( t - \tau) + n(t).$$
- Es handelt sich nach unseren Definitionen um ein verzerrungsfreies System.