Kanalcodierung/Schranken für die Blockfehlerwahrscheinlichkeit: Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
== Distanzspektrum eines linearen Codes == | == Distanzspektrum eines linearen Codes == | ||
<br> | <br> | ||
| − | Wir gehen weiterhin von einem linearen und binären $(n, \hspace{0.05cm} k)$–Blockcode $\mathcal{C}$ aus. Ein wesentliches Ziel des Codedesigns ist es, die [[Kanalcodierung/Decodierung_linearer_Blockcodes#Blockschaltbild_und_Voraussetzungen| Blockfehlerwahrscheinlichkeit]] ${\rm Pr}(\underline{u} \ne \underline{v}) = {\rm Pr}(\underline{z} \ne \underline{x})$ möglichst gering zu halten. Dies erreicht man unter anderem dadurch, dass | + | Wir gehen weiterhin von einem linearen und binären $(n, \hspace{0.05cm} k)$–Blockcode $\mathcal{C}$ aus. Ein wesentliches Ziel des Codedesigns ist es, die [[Kanalcodierung/Decodierung_linearer_Blockcodes#Blockschaltbild_und_Voraussetzungen| "Blockfehlerwahrscheinlichkeit"]] ${\rm Pr}(\underline{u} \ne \underline{v}) = {\rm Pr}(\underline{z} \ne \underline{x})$ möglichst gering zu halten. Dies erreicht man unter anderem dadurch, dass |
| − | *die minimale Distanz $d_{\rm min}$ zwischen zwei Codeworten $\underline{x}$ und $\underline{x}\hspace{0.05cm}'$ möglichst groß ist, so dass man bis zu $t = ⌊(d_{\rm min}-1)/2⌋$ Bitfehler korrigieren kann;<br> | + | *die minimale Distanz $d_{\rm min}$ zwischen zwei Codeworten $\underline{x}$ und $\underline{x}\hspace{0.05cm}'$ möglichst groß ist, so dass man bis zu $t = ⌊(d_{\rm min}-1)/2⌋$ Bitfehler korrigieren kann;<br> |
| − | *gleichzeitig | + | *gleichzeitig diese minimale Distanz $d_{\rm min}$ möglichst selten auftritt, wenn man alle zulässigen Codeworte berücksichtigt.<br><br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Wir benennen die '''Anzahl''' der Codeworte $\underline{x}\hspace{0.05cm}' \in \mathcal{C}$ mit Hamming–Distanz $i$ vom betrachteten Codewort $\underline{x}$ des gleichen Codes $\mathcal{C}$ mit $W_i(\underline{x})$, wobei gilt: | + | $\text{Definition:}$ Wir benennen die '''Anzahl''' der Codeworte $\underline{x}\hspace{0.05cm}' \in \mathcal{C}$ mit Hamming–Distanz $i$ vom betrachteten Codewort $\underline{x}$ des gleichen Codes $\mathcal{C}$ mit $W_i(\underline{x})$, wobei gilt: |
::<math>W_i(\underline{x}) = \big \vert \hspace{0.05cm} \left \{ | ::<math>W_i(\underline{x}) = \big \vert \hspace{0.05cm} \left \{ | ||
| Zeile 22: | Zeile 22: | ||
) = i \right \} \hspace{0.05cm} \big \vert\hspace{0.05cm}.</math> | ) = i \right \} \hspace{0.05cm} \big \vert\hspace{0.05cm}.</math> | ||
| − | *Die Betragsstriche kennzeichnen hierbei die Anzahl der Codeworte $\underline{x}\hspace{0.05cm}'$, die die Bedingung $d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}\hspace{0.05cm}' | + | *Die Betragsstriche kennzeichnen hierbei die Anzahl der Codeworte $\underline{x}\hspace{0.05cm}'$, die die Bedingung $d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}\hspace{0.05cm}' |
) = i $ erfüllen. | ) = i $ erfüllen. | ||
| − | *Man bezeichnet diesen Wert auch als '''Vielfachheit''' (englisch: | + | |
| + | *Man bezeichnet diesen Wert auch als '''Vielfachheit''' (englisch: "Multiplicity").}} | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ Wir betrachten den $(5, \, 2)$–Blockcode $\mathcal{C}$ mit der Generatormatrix | $\text{Beispiel 1:}$ Wir betrachten den $(5, \, 2)$–Blockcode $\mathcal{C}$ mit der Generatormatrix | ||
| − | + | [[Datei:P ID2365 KC T 1 6 S1 neu.png|right|frame|Hamming–Distanzen zwischen allen Codeworten|class=fit]] | |
:<math>{ \boldsymbol{\rm G} } | :<math>{ \boldsymbol{\rm G} } | ||
= \begin{pmatrix} | = \begin{pmatrix} | ||
| Zeile 49: | Zeile 49: | ||
<br clear=all> | <br clear=all> | ||
| − | Nicht nur in diesem Beispiel, sondern bei jedem linearen Code ergeben sich für jedes Codewort die gleichen Vielfachheiten $W_i$. Da zudem das Nullwort $\underline{0} = (0, 0,\text{ ...} \hspace{0.05cm}, 0)$ Bestandteil eines jeden linearen Binärcodes ist, lässt sich die obige Definition auch wie folgt formulieren:<br> | + | Nicht nur in diesem Beispiel, sondern bei jedem linearen Code ergeben sich für jedes Codewort die gleichen Vielfachheiten $W_i$. Da zudem das Nullwort $\underline{0} = (0, 0,\text{ ...} \hspace{0.05cm}, 0) $ Bestandteil eines jeden linearen Binärcodes ist, lässt sich die obige Definition auch wie folgt formulieren:<br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Das '''Distanzspektrum''' eines linearen binären $(n, \hspace{0.03cm} k)$–Blockcodes ist die Menge $\{W_i \}$ mit $i = 0, 1,$ ... , $n$. Hierbei gibt $W_i$ die Anzahl der Codeworte $\underline{x} \in \mathcal{C}$ mit Hamming–Gewicht $w_{\rm H}(\underline{x}) = i$ an. | + | $\text{Definition:}$ Das '''Distanzspektrum''' eines linearen binären $(n, \hspace{0.03cm} k)$–Blockcodes ist die Menge $\{W_i \}$ mit $i = 0, 1,$ ... , $n$. |
| + | *Hierbei gibt $W_i$ die Anzahl der Codeworte $\underline{x} \in \mathcal{C}$ mit Hamming–Gewicht $w_{\rm H}(\underline{x}) = i$ an. | ||
| − | Oft beschreibt man die Menge $\hspace{0.05cm}\{W_i \}\hspace{0.05cm}$ auch als Polynom mit einer Pseudovariablen $X$: | + | *Oft beschreibt man die Menge $\hspace{0.05cm}\{W_i \}\hspace{0.05cm}$ auch als Polynom mit einer Pseudovariablen $X$: |
::<math>\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} | ::<math>\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} | ||
| − | W(X) = \sum_{i=0 }^{n} W_i \cdot | + | W(X) = \sum_{i=0 }^{n} W_i \cdot X^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.</math> |
| − | Man bezeichnet $W(X)$ auch als '''Gewichtsfunktion''' (englisch: | + | *Man bezeichnet $W(X)$ auch als '''Gewichtsfunktion''' $($englisch: "Weight Enumerator Function", $\rm WEF)$.}}<br> |
| − | Beispielsweise lautet die Gewichtsfunktion des $(5, \hspace{0.02cm} 2)$–Codes $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ von $\text{Beispiel 1}$: | + | *Beispielsweise lautet die Gewichtsfunktion des $(5, \hspace{0.02cm} 2)$–Codes $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ von $\text{Beispiel 1}$: |
::<math>W(X) = 1 + 2 \cdot X^{3} + X^{4}\hspace{0.05cm}.</math> | ::<math>W(X) = 1 + 2 \cdot X^{3} + X^{4}\hspace{0.05cm}.</math> | ||
| − | Wie aus der [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Einige_Eigenschaften_des_.287.2C_4.2C_3.29.E2.80.93Hamming.E2.80.93Codes |Tabelle seiner Codeworte]] hervorgeht, erhält man für den $(7, \hspace{0.02cm}4, \hspace{0.02cm}3)$–Hamming–Code: | + | *Wie aus der [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Einige_Eigenschaften_des_.287.2C_4.2C_3.29.E2.80.93Hamming.E2.80.93Codes |"Tabelle seiner Codeworte"]] hervorgeht, erhält man für den $(7, \hspace{0.02cm}4, \hspace{0.02cm}3)$–Hamming–Code: |
::<math>W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.</math> | ::<math>W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.</math> | ||
| − | Die Überführung des Distanzspektrums $\hspace{0.01cm}\{W_i \}\hspace{0.01cm}$ in die Gewichtsfunktion $W(X)$ bietet zudem bei manchen Aufgabenstellungen große numerische Vorteile. Ist beispielsweise die | + | *Die Überführung des Distanzspektrums $\hspace{0.01cm}\{W_i \}\hspace{0.01cm}$ in die Gewichtsfunktion $W(X)$ bietet zudem bei manchen Aufgabenstellungen große numerische Vorteile. Ist beispielsweise die "Weight Enumerator Function" $W(X)$ eines $(n, \hspace{0.03cm} k)$–Blockcodes $\mathcal{C}$ bekannt, so gilt für den hierzu [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Darstellung_von_SPC_und_RC_als_duale_Codes|"dualen $(n, \hspace{0.03cm} n-k)$–Code"]] $\mathcal{C}_{\rm Dual}$: |
::<math>W_{\rm Dual}(X) = \frac{(1+X)^n}{2^k} \cdot W \left ( \frac{1-X}{1+X} \right )\hspace{0.05cm}.</math> | ::<math>W_{\rm Dual}(X) = \frac{(1+X)^n}{2^k} \cdot W \left ( \frac{1-X}{1+X} \right )\hspace{0.05cm}.</math> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ Gesucht ist die Gewichtsfunktion $W(X)$ des [[Kanalcodierung/Beispiele_bin%C3%A4rer_Blockcodes#Single_Parity.E2.80.93check_Codes|Single Parity–check Codes]] mit $n = 6$, $k = 5$ ⇒ $\text{SPC (6, 5)}$. | + | $\text{Beispiel 2:}$ Gesucht ist die Gewichtsfunktion $W(X)$ des [[Kanalcodierung/Beispiele_bin%C3%A4rer_Blockcodes#Single_Parity.E2.80.93check_Codes|"Single Parity–check Codes"]] mit $n = 6$, $k = 5$ ⇒ $\text{SPC (6, 5)}$. Man erhält diese durch Vergleich aller $2^5 = 32$ Codeworte mit dem Nullwort: |
| − | |||
| − | Man erhält diese durch Vergleich aller $2^5 = 32$ Codeworte mit dem Nullwort: | ||
::<math>W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = 1 + 15 \cdot X^{2} + 15 \cdot X^{4} + X^{6}\hspace{0.05cm}.</math> | ::<math>W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = 1 + 15 \cdot X^{2} + 15 \cdot X^{4} + X^{6}\hspace{0.05cm}.</math> | ||
| Zeile 91: | Zeile 90: | ||
== Union Bound der Blockfehlerwahrscheinlichkeit == | == Union Bound der Blockfehlerwahrscheinlichkeit == | ||
<br> | <br> | ||
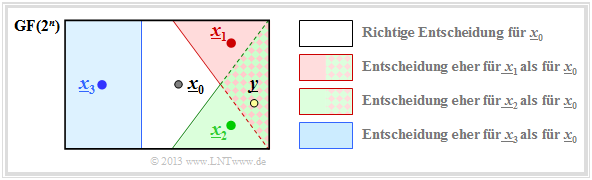
| − | Wir betrachten wie im $\text{Beispiel 1}$ | + | Wir betrachten wie im $\text{Beispiel 1}$ den $(5, \hspace{0.02cm} 2)$–Blockcode $\mathcal{C} = \{\underline{x}_0, \underline{x}_1, \underline{x}_2, \underline{x}_3 \}$ und setzen voraus, dass das Codewort $\underline{x}_0$ gesendet wurde. Die Grafik verdeutlicht den Sachverhalt. |
| + | |||
| + | [[Datei:P ID2366 KC T 1 6 S2b v2.png|right|frame|Zur Herleitung der Union Bound |class=fit]] | ||
| − | + | *Im fehlerfreien Fall würde dann der Codewortschätzer $\underline{z} = \underline{x}_0$ liefern. | |
| − | + | *Andernfalls käme es zu einem Blockfehler: $($das heißt: $\underline{z} \ne \underline{x}_0$ und dementsprechend $\underline{v} \ne \underline{u}_0)$ mit der Wahrscheinlichkeit | |
| − | : | + | :$${\rm Pr(block\:error)} = {\rm Pr}\left (\big [\underline{x}_{\hspace{0.02cm}0} \hspace{-0.07cm}\mapsto \hspace{-0.07cm}\underline{x}_{\hspace{0.02cm}1}\big ] \hspace{-0.07cm}\cup\hspace{-0.07cm}\big [\underline{x}_{\hspace{0.02cm}0} \hspace{-0.07cm}\mapsto \hspace{-0.07cm} \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{-0.07cm}\cup\hspace{-0.07cm}\big [\underline{x}_{\hspace{0.02cm}0} \hspace{-0.07cm}\mapsto \hspace{-0.07cm} \underline{x}_{\hspace{0.02cm}3}\big ] \right ).$$ |
| − | |||
| − | Das Ereignis „Verfälschung von $\underline{x}_0$ nach $\underline{x}_1$” tritt für ein gegebenes Empfangswort $\underline{y}$ entsprechend der [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Definitionen_der_verschiedenen_Optimalempf.C3.A4nger|Maximum–Likelihood–Entscheidungsregel]] | + | ⇒ Das Ereignis „Verfälschung von $\underline{x}_0$ nach $\underline{x}_1$” tritt für ein gegebenes Empfangswort $\underline{y}$ entsprechend der [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Definitionen_der_verschiedenen_Optimalempf.C3.A4nger|"blockweisen Maximum–Likelihood–Entscheidungsregel"]] genau dann ein, wenn für die bedingte Wahrscheinlichkeitsdichtefunktion gilt: |
::<math>\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} | ::<math>\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} | ||
| Zeile 106: | Zeile 106: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Da $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] $nicht notwendigerweise | + | |
| + | ⇒ Da die Ereignisse $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] $nicht notwendigerweise "disjunkt" sind, die sich somit gegenseitig ausschließen würden, ist die [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Vereinigungsmenge| "Wahrscheinlichkeit der Vereinigungsmenge"]] kleiner oder gleich der Summe der Einzelwahrscheinlichkeiten: | ||
:<math>{\rm Pr(Blockfehler)} \le {\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}+\hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}+ \hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \hspace{0.05cm}.</math> | :<math>{\rm Pr(Blockfehler)} \le {\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}+\hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}+ \hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \hspace{0.05cm}.</math> | ||
| − | Man nennt diese obere Schranke für die | + | ⇒ Man nennt diese obere Schranke für die Blockfehlerwahrscheinlichkeit die '''Union Bound'''. Diese wurde schon im Kapitel [[Digitalsignalübertragung/Approximation_der_Fehlerwahrscheinlichkeit#Union_Bound_-_Obere_Schranke_f.C3.BCr_die_Fehlerwahrscheinlichkeit|"Approximation der Fehlerwahrscheinlichkeit"]] des Buches „Digitalsignalübertragung” verwendet.<br> |
| − | Wir verallgemeinern und formalisieren diese Ergebnisse unter der Voraussetzung, dass sowohl $\underline{x}$ als auch $\underline{x}\hspace{0.05cm}'$ zum Code $\mathcal{C}$ gehören. | + | Wir verallgemeinern und formalisieren diese Ergebnisse unter der Voraussetzung, dass sowohl $\underline{x}$ als auch $\underline{x}\hspace{0.05cm}'$ zum Code $\mathcal{C}$ gehören. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| Zeile 120: | Zeile 121: | ||
::$${\rm Pr(Blockfehler)} = {\rm Pr} \left ( \bigcup_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm}\big [\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \right )\hspace{0.05cm},$$ | ::$${\rm Pr(Blockfehler)} = {\rm Pr} \left ( \bigcup_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm}\big [\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \right )\hspace{0.05cm},$$ | ||
| − | *Obere Schranke | + | *Obere Schranke entsprechend der "$\text{Union Bound}$": |
::$${\rm Pr(Union \hspace{0.15cm}Bound)} \le \sum_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm} {\rm Pr}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \hspace{0.05cm},$$ | ::$${\rm Pr(Union \hspace{0.15cm}Bound)} \le \sum_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm} {\rm Pr}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \hspace{0.05cm},$$ | ||
| − | * $\text{Paarweise Fehlerwahrscheinlichkeit}$ (nach dem | + | * $\text{Paarweise Fehlerwahrscheinlichkeit}$ (nach dem Maximum–a–posteriori– bzw. Maximum–Likelihood–Kriterium): |
::$${\rm Pr}\hspace{0.02cm}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] = {\rm Pr} \big [ | ::$${\rm Pr}\hspace{0.02cm}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] = {\rm Pr} \big [ | ||
Version vom 4. August 2022, 14:07 Uhr
Inhaltsverzeichnis
Distanzspektrum eines linearen Codes
Wir gehen weiterhin von einem linearen und binären $(n, \hspace{0.05cm} k)$–Blockcode $\mathcal{C}$ aus. Ein wesentliches Ziel des Codedesigns ist es, die "Blockfehlerwahrscheinlichkeit" ${\rm Pr}(\underline{u} \ne \underline{v}) = {\rm Pr}(\underline{z} \ne \underline{x})$ möglichst gering zu halten. Dies erreicht man unter anderem dadurch, dass
- die minimale Distanz $d_{\rm min}$ zwischen zwei Codeworten $\underline{x}$ und $\underline{x}\hspace{0.05cm}'$ möglichst groß ist, so dass man bis zu $t = ⌊(d_{\rm min}-1)/2⌋$ Bitfehler korrigieren kann;
- gleichzeitig diese minimale Distanz $d_{\rm min}$ möglichst selten auftritt, wenn man alle zulässigen Codeworte berücksichtigt.
$\text{Definition:}$ Wir benennen die Anzahl der Codeworte $\underline{x}\hspace{0.05cm}' \in \mathcal{C}$ mit Hamming–Distanz $i$ vom betrachteten Codewort $\underline{x}$ des gleichen Codes $\mathcal{C}$ mit $W_i(\underline{x})$, wobei gilt:
- \[W_i(\underline{x}) = \big \vert \hspace{0.05cm} \left \{ \underline{x} \hspace{0.05cm}, \underline{x}{\hspace{0.05cm}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm}\vert\hspace{0.1cm} d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}\hspace{0.05cm}' ) = i \right \} \hspace{0.05cm} \big \vert\hspace{0.05cm}.\]
- Die Betragsstriche kennzeichnen hierbei die Anzahl der Codeworte $\underline{x}\hspace{0.05cm}'$, die die Bedingung $d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}\hspace{0.05cm}' ) = i $ erfüllen.
- Man bezeichnet diesen Wert auch als Vielfachheit (englisch: "Multiplicity").
$\text{Beispiel 1:}$ Wir betrachten den $(5, \, 2)$–Blockcode $\mathcal{C}$ mit der Generatormatrix
\[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 &0 &1 &1 &0 \\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.\]
Die Tabelle zeigt die Hamming–Distanzen
- zwischen allen Codeworten $\underline{x}_i$
- zu den Bezugsworten $\underline{x}_0$, ... , $\underline{x}_3$.
Man erkennt: Unabhängig vom Bezugswort $\underline{x}_i$ gilt:
- \[W_0 = 1 \hspace{0.05cm}, \hspace{0.5cm}W_1 = W_2 = 0 \hspace{0.05cm},\hspace{0.5cm} W_3 = 2 \hspace{0.05cm},\hspace{0.5cm} W_4 = 1\]
- \[ \Rightarrow\hspace{0.3cm} d_{\rm min} = 3\hspace{0.05cm}.\]
Nicht nur in diesem Beispiel, sondern bei jedem linearen Code ergeben sich für jedes Codewort die gleichen Vielfachheiten $W_i$. Da zudem das Nullwort $\underline{0} = (0, 0,\text{ ...} \hspace{0.05cm}, 0) $ Bestandteil eines jeden linearen Binärcodes ist, lässt sich die obige Definition auch wie folgt formulieren:
$\text{Definition:}$ Das Distanzspektrum eines linearen binären $(n, \hspace{0.03cm} k)$–Blockcodes ist die Menge $\{W_i \}$ mit $i = 0, 1,$ ... , $n$.
- Hierbei gibt $W_i$ die Anzahl der Codeworte $\underline{x} \in \mathcal{C}$ mit Hamming–Gewicht $w_{\rm H}(\underline{x}) = i$ an.
- Oft beschreibt man die Menge $\hspace{0.05cm}\{W_i \}\hspace{0.05cm}$ auch als Polynom mit einer Pseudovariablen $X$:
- \[\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot X^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.\]
- Man bezeichnet $W(X)$ auch als Gewichtsfunktion $($englisch: "Weight Enumerator Function", $\rm WEF)$.
- Beispielsweise lautet die Gewichtsfunktion des $(5, \hspace{0.02cm} 2)$–Codes $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ von $\text{Beispiel 1}$:
- \[W(X) = 1 + 2 \cdot X^{3} + X^{4}\hspace{0.05cm}.\]
- Wie aus der "Tabelle seiner Codeworte" hervorgeht, erhält man für den $(7, \hspace{0.02cm}4, \hspace{0.02cm}3)$–Hamming–Code:
- \[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]
- Die Überführung des Distanzspektrums $\hspace{0.01cm}\{W_i \}\hspace{0.01cm}$ in die Gewichtsfunktion $W(X)$ bietet zudem bei manchen Aufgabenstellungen große numerische Vorteile. Ist beispielsweise die "Weight Enumerator Function" $W(X)$ eines $(n, \hspace{0.03cm} k)$–Blockcodes $\mathcal{C}$ bekannt, so gilt für den hierzu "dualen $(n, \hspace{0.03cm} n-k)$–Code" $\mathcal{C}_{\rm Dual}$:
- \[W_{\rm Dual}(X) = \frac{(1+X)^n}{2^k} \cdot W \left ( \frac{1-X}{1+X} \right )\hspace{0.05cm}.\]
$\text{Beispiel 2:}$ Gesucht ist die Gewichtsfunktion $W(X)$ des "Single Parity–check Codes" mit $n = 6$, $k = 5$ ⇒ $\text{SPC (6, 5)}$. Man erhält diese durch Vergleich aller $2^5 = 32$ Codeworte mit dem Nullwort:
- \[W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = 1 + 15 \cdot X^{2} + 15 \cdot X^{4} + X^{6}\hspace{0.05cm}.\]
Unter Berücksichtigung obiger Gleichung kommt man sehr viel schneller zum gleichen Ergebnis:
- Der zu $\text{SPC (6, 5)}$ duale Code ist der Repetition Code $\text{RC (6, 1)}$ mit nur zwei Codeworten $(0, 0, 0, 0, 0, 0)$ und $(1, 1, 1, 1, 1, 1)$:
- \[W_{\rm RC\hspace{0.03cm}(6,\hspace{0.08cm}1)}(X) = 1 + X^{6}\hspace{0.05cm}.\]
- Daraus folgt für die Gewichtsfunktion des $\text{SPC (6, 5)}$ nach obiger Gleichung mit $k = 1$:
- \[W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = \frac{(1+X)^6}{2^1} \cdot W \left [1 \hspace{-0.05cm}+\hspace{-0.05cm} \left ( \frac {1\hspace{-0.05cm}-\hspace{-0.05cm}X}{1\hspace{-0.05cm}+\hspace{-0.05cm}X}\right )^6 \right ] = 1/2 \cdot \big [( 1\hspace{-0.05cm}+\hspace{-0.05cm}X) ^6 \hspace{-0.05cm}+\hspace{-0.05cm} ( 1-X) ^6 \big ] = 1 \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{2} \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{4} \hspace{-0.05cm}+\hspace{-0.05cm} X^{6}\hspace{0.05cm}.\]
Union Bound der Blockfehlerwahrscheinlichkeit
Wir betrachten wie im $\text{Beispiel 1}$ den $(5, \hspace{0.02cm} 2)$–Blockcode $\mathcal{C} = \{\underline{x}_0, \underline{x}_1, \underline{x}_2, \underline{x}_3 \}$ und setzen voraus, dass das Codewort $\underline{x}_0$ gesendet wurde. Die Grafik verdeutlicht den Sachverhalt.
- Im fehlerfreien Fall würde dann der Codewortschätzer $\underline{z} = \underline{x}_0$ liefern.
- Andernfalls käme es zu einem Blockfehler: $($das heißt: $\underline{z} \ne \underline{x}_0$ und dementsprechend $\underline{v} \ne \underline{u}_0)$ mit der Wahrscheinlichkeit
- $${\rm Pr(block\:error)} = {\rm Pr}\left (\big [\underline{x}_{\hspace{0.02cm}0} \hspace{-0.07cm}\mapsto \hspace{-0.07cm}\underline{x}_{\hspace{0.02cm}1}\big ] \hspace{-0.07cm}\cup\hspace{-0.07cm}\big [\underline{x}_{\hspace{0.02cm}0} \hspace{-0.07cm}\mapsto \hspace{-0.07cm} \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{-0.07cm}\cup\hspace{-0.07cm}\big [\underline{x}_{\hspace{0.02cm}0} \hspace{-0.07cm}\mapsto \hspace{-0.07cm} \underline{x}_{\hspace{0.02cm}3}\big ] \right ).$$
⇒ Das Ereignis „Verfälschung von $\underline{x}_0$ nach $\underline{x}_1$” tritt für ein gegebenes Empfangswort $\underline{y}$ entsprechend der "blockweisen Maximum–Likelihood–Entscheidungsregel" genau dann ein, wenn für die bedingte Wahrscheinlichkeitsdichtefunktion gilt:
- \[\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} f(\underline{x}_{\hspace{0.02cm}0}\hspace{0.02cm} | \hspace{0.05cm}\underline{y}) < f(\underline{x}_{\hspace{0.02cm}1}\hspace{0.02cm} | \hspace{0.05cm}\underline{y}) \hspace{0.05cm}.\]
⇒ Da die Ereignisse $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] $nicht notwendigerweise "disjunkt" sind, die sich somit gegenseitig ausschließen würden, ist die "Wahrscheinlichkeit der Vereinigungsmenge" kleiner oder gleich der Summe der Einzelwahrscheinlichkeiten:
\[{\rm Pr(Blockfehler)} \le {\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}+\hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}+ \hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \hspace{0.05cm}.\]
⇒ Man nennt diese obere Schranke für die Blockfehlerwahrscheinlichkeit die Union Bound. Diese wurde schon im Kapitel "Approximation der Fehlerwahrscheinlichkeit" des Buches „Digitalsignalübertragung” verwendet.
Wir verallgemeinern und formalisieren diese Ergebnisse unter der Voraussetzung, dass sowohl $\underline{x}$ als auch $\underline{x}\hspace{0.05cm}'$ zum Code $\mathcal{C}$ gehören.
$\text{Dann gelten folgende Berechnungsvorschriften:}$
- $\rm Blockfehlerwahrscheinlichkeit$:
- $${\rm Pr(Blockfehler)} = {\rm Pr} \left ( \bigcup_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm}\big [\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \right )\hspace{0.05cm},$$
- Obere Schranke entsprechend der "$\text{Union Bound}$":
- $${\rm Pr(Union \hspace{0.15cm}Bound)} \le \sum_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm} {\rm Pr}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \hspace{0.05cm},$$
- $\text{Paarweise Fehlerwahrscheinlichkeit}$ (nach dem Maximum–a–posteriori– bzw. Maximum–Likelihood–Kriterium):
- $${\rm Pr}\hspace{0.02cm}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] = {\rm Pr} \big [ f(\underline{x}\hspace{0.05cm}\vert \hspace{0.05cm}\underline{y}) \le f(\underline{x}\hspace{0.05cm}'\hspace{0.05cm} \vert \hspace{0.05cm}\underline{y}) \big ] \hspace{0.05cm}.$$
Auf den nächsten Seiten werden diese Ergebnisse auf verschiedene Kanäle angewendet.
Union Bound für das BSC–Modell
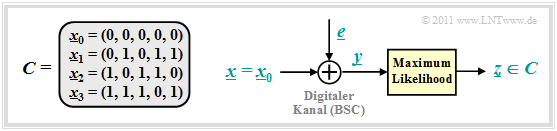
Wir betrachten weiterhin den beispielhaften $(5, \hspace{0.02cm} 2)$–Code: $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ und für den digitalen Kanal verwenden wir das BSC–Modell (Binary Symmetric Channel ):
- \[{\rm Pr}(y = 1 \hspace{0.05cm} | \hspace{0.05cm}x = 0 ) = {\rm Pr}(y = 0 \hspace{0.05cm} | \hspace{0.05cm}x = 1 ) = {\rm Pr}(e = 1) = \varepsilon \hspace{0.05cm},\]
- \[{\rm Pr}(y = 0 \hspace{0.05cm} | \hspace{0.05cm}x = 0 ) = {\rm Pr}(y = 1 \hspace{0.05cm} | \hspace{0.05cm}x = 1 ) = {\rm Pr}(e = 0) = 1 -\varepsilon \hspace{0.05cm}.\]
Dann gilt (siehe nachfolgende Grafik):
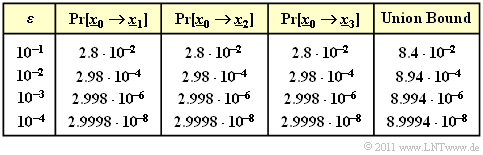
- Die Codeworte $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_1 = (0, 1, 0, 1, 1)$ unterscheiden sich in $d = 3$ Bit, wobei $d$ die Hamming–Distanz zwischen $\underline{x}_0$ und $\underline{x}_1$ angibt.
- Ein falsches Decodierergebnis $\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] $ erhält man immer dann, wenn mindestens zwei der drei Bit an den Bitpositionen 2, 4 und 5 verfälscht werden.
- Die Bitpositionen 1 und 3 spielen hier dagegen keine Rolle, da diese für $\underline{x}_0$ und $\underline{x}_1$ gleich sind.
Da der betrachtete Code $t = ⌊(d-1)/2⌋ = 1$ Fehler korrigieren kann, gilt:
- \[{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i=t+1 }^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} = {3 \choose 2} \cdot \varepsilon^{2} \cdot (1 - \varepsilon) + {3 \choose 3} \cdot \varepsilon^{3} =3 \cdot \varepsilon^2 \cdot (1 - \varepsilon) + \varepsilon^3 = {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big]\hspace{0.05cm}.\]
Hierbei ist berücksichtigt, dass sich $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_2 = (1, 0, 1, 1, 0)$ ebenfalls in drei Bitpositionen unterscheiden.
Die Codeworte $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_3 = (1, 1, 1, 0, 1)$ unterscheiden sich dagegen in vier Bitpositionen:
- Zu einer falschen Decodierung des Blocks kommt es deshalb mit Sicherheit, wenn vier oder drei Bit verfälscht werden.
- Eine Verfälschung von zwei Bit hat mit $50$–prozentiger Wahrscheinlichkeit ebenfalls einen Blockfehler zur Folge, wenn man hierfür eine Zufallsentscheidung voraussetzt.
- \[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big] = \varepsilon^4 + 4 \cdot \varepsilon^3 \cdot (1 - \varepsilon) + {1}/{2} \cdot 6 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^2 \hspace{0.05cm}.\]
Daraus ergibt sich für die „Union Bound”:
- \[{\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}\big] +{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}\big] \ge {\rm Pr(Blockfehler)} .\]
$\text{Beispiel 3:}$ In der Tabelle sind die Ergebnisse für verschiedene Werte des BSC–Parameters $\varepsilon$ zusammengefasst.
Zu erwähnen ist, dass die völlig unterschiedlich zu berechnenden Wahrscheinlichkeiten ${\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}\big]$ und ${\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}3}\big]$ genau das gleiche numerische Ergebnis liefern.
Die obere Schranke nach Bhattacharyya
Eine weitere obere Schranke für die Blockfehlerwahrscheinlichkeit wurde von Bhattacharyya angegeben:
- \[{\rm Pr(Blockfehler)} \le W(X = \beta) -1 = {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
Hierzu ist anzumerken:
- $W(X)$ ist die oben definierte Gewichtsfunktion, die den verwendeten Kanalcode charakterisiert.
- Der Bhattacharyya–Parameter $\beta$ kennzeichnet den digitalen Kanal. Beispielsweise gilt:
- \[\beta = \left\{ \begin{array}{c} \lambda \\ \sqrt{4 \cdot \varepsilon \cdot (1- \varepsilon)}\\ {\rm e}^{- R \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm B}/N_0} \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}BEC-Modell},\\ {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}BSC-Modell}, \\ {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}AWGN-Modell}. \end{array}\]
- Die Bhattacharyya–Schranke liegt stets (und meist deutlich) oberhalb der Kurve für die „Union Bound”. Mit dem Ziel, eine für alle Kanäle einheitliche Schranke zu finden, müssen hier sehr viel gröbere Abschätzungen vorgenommen werden als für die „Union Bound”.
Wir beschränken uns hier auf die Bhattacharyya–Schranke für das BSC–Modell. Für dessen paarweise Verfälschungswahrscheinlichkeit wurde vorne hergeleitet:
- \[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] = \sum_{i= \left\lfloor (d-1)/2 \right\rfloor}^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} = \sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i}\hspace{0.05cm}.\]
- Hierbei kennzeichnet $\varepsilon = {\rm Pr}(y = 1\hspace{0.04cm}|\hspace{0.04cm} x = 0) = {\rm Pr}(y = 0\hspace{0.04cm}|\hspace{0.04cm} x = 1)< 0.5$ das Kanalmodell.
- $d = d_{\rm H}(\underline{x}_0,\, \underline{x}_1)$ gibt die Hamming–Distanz der betrachteten Codeworte an.
Um zur Bhattacharyya–Schranke zu kommen, müssen folgende Abschätzungen getroffen werden:
- Für alle $i < d$ gilt $\varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} \le (1 - \varepsilon)^{d/2}$:
- \[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] \le \big[\varepsilon \cdot (1 - \varepsilon)\big]^{d/2} \cdot \sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \hspace{0.05cm}.\]
- Änderung bezüglich der unteren Grenze der Laufvariablen $i$:
- \[\sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \hspace{0.15cm} < \hspace{0.15cm} \sum_{i= 0 }^{d} {d \choose i} = 2^d\hspace{0.05cm}, \hspace{0.2cm}\beta = 2 \cdot \sqrt{\varepsilon \cdot (1 - \varepsilon)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] = \beta^{d} \hspace{0.05cm}.\]
- Umsortierung gemäß den Hamming–Gewichten $W_i$ (Hamming–Distanz $d = i$ kommt $W_i$ mal vor):
- \[{\rm Pr(Blockfehler)} \hspace{0.1cm} \le \hspace{0.1cm} \sum_{i= 1 }^{n} W_i \cdot \beta^{i} = 1 + W_1 \cdot \beta + W_2 \cdot \beta^2 + \hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ W_n \cdot \beta^n \hspace{0.05cm}.\]
- Mit der Gewichtsfunktion $W(X)= 1 + W_1 \cdot X + W_2 \cdot X^2 + \text{...} + W_n \cdot X^n$:
- \[{\rm Pr(Blockfehler)} \le W(X = \beta) -1= {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
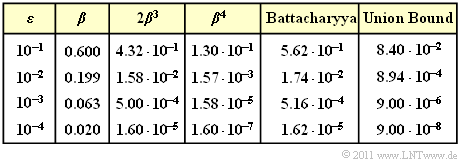
$\text{Beispiel 4:}$ In der Tabelle sind die Bhattacharyya–Ergebnisse für verschiedene Werte des BSC–Parameters $\varepsilon$ zusammengefasst, gültig für den beispielhaften $\text{(5, 2)}$–Code.
Für diesen gilt:
- $$W_0 = 1, \ \ W_1 = W_2 = 0, \ \ W_3 = 2, \ \ W_4 = 1$$
- $$\Rightarrow\hspace{0.3cm} W(X) = 1 + 2 \cdot X^3 + X^4.$$
Damit kann die Bhattacharyya–Schranke berechnet werden:
- \[ {\rm Pr(Bhattacharyya)} = W(\beta) -1 = 2 \cdot \beta^3 + \beta^4\hspace{0.05cm}.\]
Diese stellt eine (oft grobe) Schranke für die Blockfehlerwahrscheinlichkeit dar:
- \[ {\rm Pr(Blockfehler)} \le {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
$\text{Fazit:}$ Basierend auf dem $\text{Beispiel 3}$ und dem $\text{Beispiel 4}$ (auf dieser Seite) für den einfachen $\text{(5, 2)}$–Blockcode, der allerdings wenig praxisrelevant ist, sowie im Vorgriff auf das $\text{Beispiel 5}$ (auf der nächsten Seite) für den $\text{(7, 4, 3)}$–Hamming–Code fassen wir zusammen:
- Die Blockfehlerwahrscheinlichkeit eines Codiersystems ist oft analytisch nicht angebbar und muss per Simulation ermittelt werden. Gleiches gilt für die Bitfehlerwahrscheinlichkeit.
- Die Union Bound liefert eine obere Schranke für die Blockfehlerwahrscheinlichkeit. Bei vielen Anwendungen (insbesondere bei kurzen Codes) liegt die Union Bound nur geringfügig über der tatsächlichen Fehlerwahrscheinlichkeit.
- Die Bhattacharyya–Schranke liegt beim BEC–Kanal etwa um den Faktor $2$ oberhalb der Union Bound – siehe Aufgabe 1.14. Beim BSC– und beim AWGN–Kanal ist der Abstand deutlich größer. Der Faktor $10$ (und mehr) ist keine Seltenheit.
- Die Bhattacharyya–Schranke $W(\beta) - 1$ wirkt auf den ersten Blick sehr einfach. Trotzdem benötigt man auch hier Kenntnis über die genaue Gewichtsfunktion $W(\xi)$ des Codes.
- Bei Kenntnis des vorliegenden Übertragungskanals (BEC, BSC, AWGN oder Abwandlungen hiervon) und dessen Parameter spricht somit vom Aufwand her nichts dagegen, gleich die (genauere) „Union Bound” als obere Schranke für die Blockfehlerwahrscheinlichkeit zu verwenden.
Schranken für den (7, 4, 3)–Hamming–Code beim AWGN–Kanal
Abschließend betrachten wir die Blockfehlerwahrscheinlichkeit und deren Schranken („Union Bound” und „Bhattacharyya–Schranke” ) für die folgende Konfiguration:
- AWGN–Kanal, gekennzeichnet durch den Quotienten $E_{\rm B}/N_0$,
- Hamming–Code $\text{HC(7, 4, 3)}$ ⇒ $R = 4/7$, $W(X)-1 = 7 \cdot X^3 + 7 \cdot X^4 + X^7$,
- „Soft–Decision” nach dem Maximum–Likelihood–Kriterium.
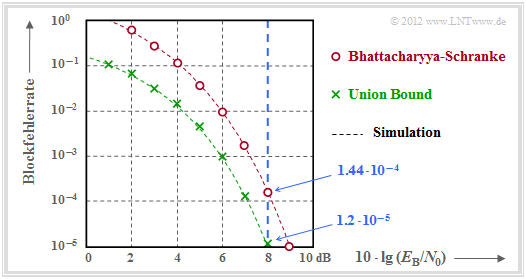
$\text{Beispiel 5:}$ Die Ergebnisse sind in der Grafik zusammengefasst.
- Im Gegensatz zur Grafik im Abschnitt Codiergewinn – Bitfehlerrate bei AWGN ist hier die Blockfehlerrate angegeben und nicht die Bitfehlerrate.
- Näherungsweise ist Letztere um den Faktor $d_{\rm min}/k$ kleiner, falls wie hier $d_{\rm min}< k$ ist. Im vorliegenden Beispiel gilt $d_{\rm min}/k = 0.75$.
- Berechnet wurden nur die Punkte für ganzzahlige $\rm dB$–Werte. Die gestrichelten Linien wurden interpoliert.
- Die rechts angegebenen (blauen) Zahlenwerte gelten für $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$ ⇒ $E_{\rm B}/N_0 \approx 6.31$ (blaue Vertikale).
Die grünen Kreuze markieren die „Union Bound”. Nach dieser gilt:
- \[{\rm Pr(Blockfehler)} \le \sum_{i= d_{\rm min} }^{n} W_i \cdot {\rm Q} \left ( \sqrt{i \cdot {2R \cdot E_{\rm B} }/{N_0} } \right ) \]
- \[\Rightarrow \hspace{0.3cm}{\rm Pr(Blockfehler)} \approx 7 \cdot {\rm Q} (4.65) + 7 \cdot {\rm Q} (5.37) + {\rm Q} (7.10) = \]
- \[\hspace{4.0cm} \approx 7 \cdot 1.66 \cdot 10^{-6} + 7 \cdot 3.93 \cdot 10^{-8}+ 10^{-9} = 1.2 \cdot 10^{-5} \hspace{0.05cm}.\]
- Die Zahlenwerte machen deutlich, dass die Union Bound im wesentlichen durch den ersten Term bestimmt wird:
- \[{\rm Pr(Union\hspace{0.15cm} Bound)} \approx W_{d_{\rm min} } \cdot {\rm Q} \left ( \sqrt{d_{\rm min} \cdot {2R \cdot E_{\rm B} }/{N_0} } \right ) = 1.16 \cdot 10^{-5} \hspace{0.05cm}.\]
- Allerdings ist diese so genannte „Truncated Union Bound” nicht mehr bei allen Anwendungen eine echte Schranke für die Blockfehlerwahrscheinlichkeit, sondern ist als Näherung zu verstehen.
- Die Bhattacharyya–Schranke ist in der Grafik durch rote Punkte markiert. Diese liegt aufgrund der stark vereinfachten Chernoff–Rubin Bound ${\rm Q}(x) \le {\rm e}^{-x^2/2}$ deutlich über der Union Bound.
- Zum Beispiel erhält man für $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$ mit $\beta = {\rm e}^{-R \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm B}/N_0} \approx 0.027$ gegenüber der Union Bound einen mehr als zehnfachen Wert:
- \[{\rm Pr(Bhattacharyya)} = W(\beta) -1 = 7 \cdot \beta^3 + 7 \cdot \beta^4 + \beta^7 \approx 1.44 \cdot 10^{-4} \hspace{0.05cm}.\]
Aufgaben zum Kapitel
Aufgabe 1.14: Bhattacharyya–Schranke für BEC
Aufgabe 1.15: Distanzspektren von HC (7, 4, 3) und HC (8, 4, 4)
Aufgabe 1.16: Fehlerwahrscheinlichkeitsschranken für AWGN
Aufgabe 1.16Z: Schranken für die Gaußsche Fehlerfunktion