Aufgaben:Aufgabe 3.8: Dreimal Faltung?: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
David (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signaldarstellung/Faltungssatz und Faltungsoperation |
| − | |||
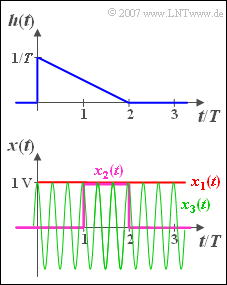
[[Datei:P_ID533__Sig_A_3_8.png|250px|right|Zur Faltungsoperation (Aufgabe A3.8)]] | [[Datei:P_ID533__Sig_A_3_8.png|250px|right|Zur Faltungsoperation (Aufgabe A3.8)]] | ||
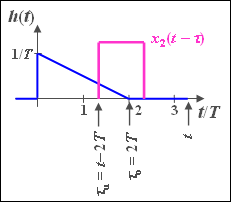
| − | Die Impulsantwort eines LZI-Systems hat im Zeitbereich zwischen 0 und | + | Die Impulsantwort eines LZI-Systems hat im Zeitbereich zwischen 0 und 2 $T$ den folgenden Verlauf: |
$$h( t ) = \frac{1}{T}\left( {1 - \frac{t}{{2T}}} \right).$$ | $$h( t ) = \frac{1}{T}\left( {1 - \frac{t}{{2T}}} \right).$$ | ||
| − | Außerhalb dieses Intervalls ist h(t) gleich 0. Die zugehörige Spektralfunktion lautet: | + | Außerhalb dieses Intervalls ist $h(t)$ gleich 0. Die zugehörige Spektralfunktion lautet: |
$$H( f ) = \frac{1}{{8\left( {{\rm{\pi }}fT} \right)^2 }} \left( {1 - {\rm{j \cdot 4\pi }}fT - {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 4\pi }}fT} } \right).$$ | $$H( f ) = \frac{1}{{8\left( {{\rm{\pi }}fT} \right)^2 }} \left( {1 - {\rm{j \cdot 4\pi }}fT - {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 4\pi }}fT} } \right).$$ | ||
| − | Zur Berechnung des sog. Gleichsignalübertragungsfaktors ⇒ H(f = 0) ist diese Gleichung nicht geeignet, da sowohl der Klammerausdruck als auch der Nenner Null werden. | + | Zur Berechnung des sog. Gleichsignalübertragungsfaktors ⇒ $H(f = 0)$ ist diese Gleichung nicht geeignet, da sowohl der Klammerausdruck als auch der Nenner Null werden. |
Es gilt aber auch: | Es gilt aber auch: | ||
| Zeile 19: | Zeile 18: | ||
An den Eingang dieses Filters werden drei verschiedene Zeitsignale angelegt (siehe Skizze): | An den Eingang dieses Filters werden drei verschiedene Zeitsignale angelegt (siehe Skizze): | ||
| − | * | + | * $x_1(t)$ ist ein Gleichsignal mit der Höhe $x_0$ = 1 V. |
| − | * | + | * $x_2(t)$ ist ein Rechtecksignal mit der Dauer $T$ und der Höhe $x_0$ = 1 V, beginnend bei $t = T$. |
| − | * | + | * $x_3(t)$ ist ein Cosinussignal mit der Frequenz $f_0 = 3/T$ und der Amplitude $x_0 = 1$ V. |
| + | |||
Hinweis: Diese Aufgabe bezieht sich auf den theoretischen Grundlagen von Kapitel 3.4. Die Thematik dieses Abschnitts wird auch in nachfolgendem Interaktionsmodul veranschaulicht: | Hinweis: Diese Aufgabe bezieht sich auf den theoretischen Grundlagen von Kapitel 3.4. Die Thematik dieses Abschnitts wird auch in nachfolgendem Interaktionsmodul veranschaulicht: | ||
| Zeile 31: | Zeile 31: | ||
{Bei welchen der drei Signale ist es zweckmäßiger, das Ausgangssignal direkt im Zeitbereich zu berechnen? | {Bei welchen der drei Signale ist es zweckmäßiger, das Ausgangssignal direkt im Zeitbereich zu berechnen? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - $y_1(t) = x_1(t) \ast h(t)$. |
| − | + | + | + $y_2(t) = x_2(t) \ast h(t)$. |
| − | - | + | - $y_3(t) = x_3(t) \ast h(t)$. |
| − | {Wie lautet das Signal | + | {Wie lautet das Signal $y_1(t)$ am Filterausgang, wenn am Eingang das Gleichsignal $x_1(t) = 1$ V anliegt? Geben Sie den Signalwert bei $t = 2T$ an. |
|type="{}"} | |type="{}"} | ||
$y_1(t=2T) = $ { 1 } V | $y_1(t=2T) = $ { 1 } V | ||
| − | {Auf welchen Zeitbereich zwischen | + | {Auf welchen Zeitbereich zwischen $t_{\text{min}}$ und $t_{\text{max}}$ ist das Ausgangssignal $y_2(t) = x_2(t) \ast h(t)$ beschränkt, d. h. ungleich 0? |
|type="{}"} | |type="{}"} | ||
$t_{\text{min}}/T = $ { 1 } | $t_{\text{min}}/T = $ { 1 } | ||
$t_{\text{max}}/T = $ { 4 } | $t_{\text{max}}/T = $ { 4 } | ||
| − | {Berechnen Sie die Werte des Signals | + | {Berechnen Sie die Werte des Signals $y_2(t)$ zu den Zeiten $t = 2T$ und $t = 3T$ |
|type="{}"} | |type="{}"} | ||
$y_2(t=2T) = $ { 0.75 } V | $y_2(t=2T) = $ { 0.75 } V | ||
$y_2(t=3T) = $ { 0.25 } V | $y_2(t=3T) = $ { 0.25 } V | ||
| − | {Wie lautet das Ausgangssignal | + | {Wie lautet das Ausgangssignal $y_3(t)$, wenn am Eingang das Cosinussignal $x_3(t)$ anliegt? Geben Sie den Signalwert bei $t$ = 0 an. |
|type="{}"} | |type="{}"} | ||
$y_2(t=3T) = $ { 0 } V | $y_2(t=3T) = $ { 0 } V | ||
| Zeile 55: | Zeile 55: | ||
</quiz> | </quiz> | ||
| + | |||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Die Signale $x_1(t)$ und $x_3(t)$ beinhalten jeweils nur eine Frequenz ( $f = 0$ bzw. $f = f_0$ ). Hier ist der Umweg über das Spektrum vorzuziehen. Beim Rechtecksignal $x_2(t)$ ist die Berechnung über die Faltung günstiger, da die Fourierrücktransformation von $Y_2(f)$ kompliziert ist ⇒ Antwort 2. |
| − | + | ||
| + | '''2.''' Das Ausgangssignal ist ebenfalls ein Gleichsignal, da folgende Gleichungen gelten: | ||
$$Y_1 (f) = X_1 (f) \cdot H(f)\quad {\rm{mit}}\quad X_1 (f) = 1\;{\rm{V}} \cdot \delta (f)$$ | $$Y_1 (f) = X_1 (f) \cdot H(f)\quad {\rm{mit}}\quad X_1 (f) = 1\;{\rm{V}} \cdot \delta (f)$$ | ||
| Zeile 69: | Zeile 71: | ||
Die Berechnung über die Faltung führt zum gleichen Ergebnis, wenn man berücksichtigt, dass das Integral über die Impulsantwort im vorliegenden Fall gleich 1 ist. | Die Berechnung über die Faltung führt zum gleichen Ergebnis, wenn man berücksichtigt, dass das Integral über die Impulsantwort im vorliegenden Fall gleich 1 ist. | ||
| − | + | ||
| + | '''3.''' Das gespiegelte Signal $x_2(–t)$ hat Signalanteile zwischen $–2T$ und $–T$. Erst eine Verschiebung um $T + \epsilon$ führt zu einer Überlappung mit $h(t)$. Hierbei bezeichnet ε eine beliebig kleine, aber positive Zeit. Ist die Verschiebung allerdings größer als $4T – \epsilon$, so liefert die Integration über das Produkt ebenfalls den Wert 0. Daraus folgt $t_{\text{min}} = T$ und $t_{\text{max}} = 4T$. | ||
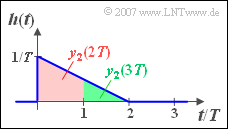
[[Datei:P_ID534__Sig_A_3_8_d.png|250px|right|Zur Faltung von Rechteck und Dreieck (ML zu Aufgabe A3.8)]] | [[Datei:P_ID534__Sig_A_3_8_d.png|250px|right|Zur Faltung von Rechteck und Dreieck (ML zu Aufgabe A3.8)]] | ||
| − | + | '''4.''' Das Ergebnis der grafischen Faltung für die Zeitpunkte $t = 2T$ und $3T$ kann man nachfolgender Skizze entnehmen. Der Wert bei $2T$ entspricht der rötlich unterlegten Fläche: | |
$$y_2( {t = 2T} ) = \frac{1}{2}\cdot ( {\frac{1}{T} + \frac{1}{{2T}}} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.75 {\rm V}} .$$ | $$y_2( {t = 2T} ) = \frac{1}{2}\cdot ( {\frac{1}{T} + \frac{1}{{2T}}} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.75 {\rm V}} .$$ | ||
| − | Die grün unterlegte Fläche kennzeichnet den Wert bei 3T: | + | Die grün unterlegte Fläche kennzeichnet den Wert bei $3T$: |
$$y_2( {t = 3T} ) = \frac{1}{2}\cdot ( {\frac{1}{2T} + 0} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.25 {\rm V}} .$$ | $$y_2( {t = 3T} ) = \frac{1}{2}\cdot ( {\frac{1}{2T} + 0} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.25 {\rm V}} .$$ | ||
| − | Um den gesamten Signalverlauf zwischen T und 4T zu berechnen, müssen drei Bereiche getrennt betrachtet werden. Zur Vereinfachung der Darstellung wird im Folgenden | + | Um den gesamten Signalverlauf zwischen $T$ und $4T$ zu berechnen, müssen drei Bereiche getrennt betrachtet werden. Zur Vereinfachung der Darstellung wird im Folgenden $x_0 = 1$ gesetzt. |
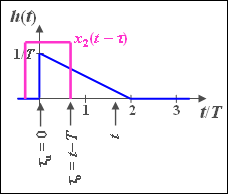
[[Datei:P_ID583__Sig_A_3_8_d1_neu.png|250px|right|Faltung im Bereich 1 (ML zu Aufgabe A3.8)]] | [[Datei:P_ID583__Sig_A_3_8_d1_neu.png|250px|right|Faltung im Bereich 1 (ML zu Aufgabe A3.8)]] | ||
| − | Im Bereich T | + | Im Bereich $T \leq t \leq 2T$ liegt die untere Integrationsgrenze fest bei $τ_u = 0$ und die obere Grenze bei $τ_0 = t – T$: |
$$y_2 (t) = \int_{\tau _u }^{\tau _0 } {h(\tau )\,{\rm{d}}\tau = \int_0^{t - T} {\frac{1}{T}} }\cdot \left( {1 - \frac{\tau }{{2T}}} \right)\,{\rm{d}}\tau .$$ | $$y_2 (t) = \int_{\tau _u }^{\tau _0 } {h(\tau )\,{\rm{d}}\tau = \int_0^{t - T} {\frac{1}{T}} }\cdot \left( {1 - \frac{\tau }{{2T}}} \right)\,{\rm{d}}\tau .$$ | ||
| Zeile 99: | Zeile 102: | ||
$$ \Rightarrow \;y_2 (t) = 1.5 \cdot \frac{t}{T} - 0.25\cdot \left( {\frac{t}{T}} \right)^2 - 1.25.$$ | $$ \Rightarrow \;y_2 (t) = 1.5 \cdot \frac{t}{T} - 0.25\cdot \left( {\frac{t}{T}} \right)^2 - 1.25.$$ | ||
| − | Zur Verifizierung betrachten wir die beiden Grenzen. Man erhält die bereits oben berechneten Werte | + | Zur Verifizierung betrachten wir die beiden Grenzen. Man erhält die bereits oben berechneten Werte $y_2(T) = 0$ und $y_2(2T) = 0.75$. |
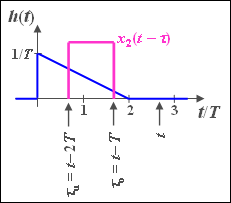
[[Datei:P_ID584__Sig_A_3_8_d2_neu.png|250px|right|Faltung im Bereich 2 (ML zu Aufgabe A3.8)]] | [[Datei:P_ID584__Sig_A_3_8_d2_neu.png|250px|right|Faltung im Bereich 2 (ML zu Aufgabe A3.8)]] | ||
| − | Im Intervall 2T | + | Im Intervall $2T \leq t \leq 3T$ liegt die obere Integrationsgrenze weiterhin bei $τ_0 = t – T$, während nun $τ_u = t – 2T$ gilt: |
$$y_2 (t) = I(t - T) - I(t - 2T) = 1.75 - 0.5 \cdot \frac{t}{T}.$$ | $$y_2 (t) = I(t - T) - I(t - 2T) = 1.75 - 0.5 \cdot \frac{t}{T}.$$ | ||
| − | Dies entspricht einem linearen Abfall mit den zwei Grenzwerten | + | Dies entspricht einem linearen Abfall mit den zwei Grenzwerten $y_2(2T) = 0.75$ und $y_2(3T) = 0.25$. |
[[Datei:P_ID585__Sig_A_3_8_d3_neu.png|250px|right|Faltung im Bereich 3 (ML zu Aufgabe A3.8)]] | [[Datei:P_ID585__Sig_A_3_8_d3_neu.png|250px|right|Faltung im Bereich 3 (ML zu Aufgabe A3.8)]] | ||
| − | Schließlich liegt im Intervall 3T | + | Schließlich liegt im Intervall $3T \leq t \leq 4T$ die obere Grenze fest bei $τ_0 = 2T$ und es gilt weiterhin $τ_u = t – 2T$: |
| − | $$y_2 (t) &= | + | $$\begin{align*}y_2 (t) &= I(2T) - I(t - 2T) \\ |
| + | &= - 2 \cdot \frac{t}{T} + 0.25\left( {\frac{t}{T}} \right)^2 + 4.\end{align*}$$ | ||
Auch hier ergeben sich die richtigen Grenzwerte | Auch hier ergeben sich die richtigen Grenzwerte | ||
| Zeile 120: | Zeile 124: | ||
$$y_2 (3T) = 0.25\quad {\rm{und}}\quad y_2 (4T) = 0.$$ | $$y_2 (3T) = 0.25\quad {\rm{und}}\quad y_2 (4T) = 0.$$ | ||
| − | + | '''5.''' Auch diese Aufgabe könnte direkt mit der Faltung gelöst werden. Da $x_3(t)$ eine gerade Funktion ist, kann hier aber nun auf die Spiegelung verzichtet werden und man erhält | |
$$y_3 (t) = \int_{ - \infty }^{ + \infty } {h(\tau ) \cdot x_3 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau = x_0 }\cdot \int_0^{2T} {h(\tau ) \cdot \cos (2{\rm{\pi }}f_0 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau .}$$ | $$y_3 (t) = \int_{ - \infty }^{ + \infty } {h(\tau ) \cdot x_3 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau = x_0 }\cdot \int_0^{2T} {h(\tau ) \cdot \cos (2{\rm{\pi }}f_0 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau .}$$ | ||
| − | Einfacher ist hier der Weg über die Spektren. X(f) besteht aus zwei Diraclinien bei | + | Einfacher ist hier der Weg über die Spektren. $X(f)$ besteht aus zwei Diraclinien bei $\pm 3f_0$. Somit muss auch nur für diese Frequenz der Frequenzgang berechnet werden: |
| − | $$H( {f = 3f_0 } ) & = | + | $$\begin{align*}H( {f = 3f_0 } ) & = \frac{1}{{72{\rm{\pi }}^{\rm{2}} }}\left[ {1 - {\rm{j}}\cdot 12{\rm{\pi }} - {\rm{cos}}( {{\rm{12\pi }}} ) + {\rm{j}}\cdot \sin ( {{\rm{12\pi }}})} \right] = \\ & = \frac{1}{{72{\rm{\pi }}^{\rm{2}} }}\left[ 1 - {\rm j}\cdot 12{\rm \pi } - 1 + {\rm j}\cdot 0 \right]= { - {\rm{j}}} \cdot \frac{1}{{6{\rm{\pi }}}}.\end{align*}$$ |
Somit lautet das Spektrum des Ausgangssignals: | Somit lautet das Spektrum des Ausgangssignals: | ||
| Zeile 132: | Zeile 136: | ||
$$Y(f) = - {\rm{j}} \cdot \frac{{x_0 }}{{{\rm{12\pi }}}}\cdot \delta \left( {f - 3f_0 } \right) + {\rm{j}} \cdot \frac{{x_0 }}{{{\rm{12\pi }}}}\cdot \delta \left( {f + 3f_0 } \right).$$ | $$Y(f) = - {\rm{j}} \cdot \frac{{x_0 }}{{{\rm{12\pi }}}}\cdot \delta \left( {f - 3f_0 } \right) + {\rm{j}} \cdot \frac{{x_0 }}{{{\rm{12\pi }}}}\cdot \delta \left( {f + 3f_0 } \right).$$ | ||
| − | Das Signal | + | Das Signal $y_3(t)$ ist somit sinusförmig mit der Amplitude $x_0/(6\pi )$. Der Signalwert bei $t$ = 0 ist 0. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | [[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | ||
Version vom 20. April 2016, 17:58 Uhr
-
[[Signaldarstellung/Faltungssatz und Faltungsoperation
Die Impulsantwort eines LZI-Systems hat im Zeitbereich zwischen 0 und 2 $T$ den folgenden Verlauf:
$$h( t ) = \frac{1}{T}\left( {1 - \frac{t}[[:Vorlage:2T]]} \right).$$
Außerhalb dieses Intervalls ist $h(t)$ gleich 0. Die zugehörige Spektralfunktion lautet:
$$H( f ) = \frac{1}{{8\left( {{\rm{\pi }}fT} \right)^2 }} \left( {1 - {\rm{j \cdot 4\pi | Zurück zum Buch]] '"`UNIQ--html-00000001-QINU`"'fT - {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 4\pi }}fT} } \right).$$
Zur Berechnung des sog. Gleichsignalübertragungsfaktors ⇒ $H(f = 0)$ ist diese Gleichung nicht geeignet, da sowohl der Klammerausdruck als auch der Nenner Null werden. Es gilt aber auch:
$$H( {f = 0} ) = \int_0^{2T} {h( t )\hspace{0.1cm}{\rm d}t = 1.}$$
An den Eingang dieses Filters werden drei verschiedene Zeitsignale angelegt (siehe Skizze):
- $x_1(t)$ ist ein Gleichsignal mit der Höhe $x_0$ = 1 V.
- $x_2(t)$ ist ein Rechtecksignal mit der Dauer $T$ und der Höhe $x_0$ = 1 V, beginnend bei $t = T$.
- $x_3(t)$ ist ein Cosinussignal mit der Frequenz $f_0 = 3/T$ und der Amplitude $x_0 = 1$ V.
Hinweis: Diese Aufgabe bezieht sich auf den theoretischen Grundlagen von Kapitel 3.4. Die Thematik dieses Abschnitts wird auch in nachfolgendem Interaktionsmodul veranschaulicht: Zur Verdeutlichung der grafischen FaltungFragebogen
Musterlösung
1. Die Signale $x_1(t)$ und $x_3(t)$ beinhalten jeweils nur eine Frequenz ( $f = 0$ bzw. $f = f_0$ ). Hier ist der Umweg über das Spektrum vorzuziehen. Beim Rechtecksignal $x_2(t)$ ist die Berechnung über die Faltung günstiger, da die Fourierrücktransformation von $Y_2(f)$ kompliziert ist ⇒ Antwort 2.2. Das Ausgangssignal ist ebenfalls ein Gleichsignal, da folgende Gleichungen gelten:
$$Y_1 (f) = X_1 (f) \cdot H(f)\quad {\rm{mit}}\quad X_1 (f) = 1\;{\rm{V}} \cdot \delta (f)$$
$$ \Rightarrow Y_1 (f) = 1\;{\rm{V}} \cdot \delta (f) \cdot H( {f = 0} ) = 1\;{\rm{V}} \cdot \delta (f).$$
$$ \Rightarrow y_1 (t) = 1\;{\rm{V}} \cdot H( {f = 0} ) \hspace{0.15 cm}\underline{= 1\;{\rm{V}}}.$$
Die Berechnung über die Faltung führt zum gleichen Ergebnis, wenn man berücksichtigt, dass das Integral über die Impulsantwort im vorliegenden Fall gleich 1 ist.
3. Das gespiegelte Signal $x_2(–t)$ hat Signalanteile zwischen $–2T$ und $–T$. Erst eine Verschiebung um $T + \epsilon$ führt zu einer Überlappung mit $h(t)$. Hierbei bezeichnet ε eine beliebig kleine, aber positive Zeit. Ist die Verschiebung allerdings größer als $4T – \epsilon$, so liefert die Integration über das Produkt ebenfalls den Wert 0. Daraus folgt $t_{\text{min}} = T$ und $t_{\text{max}} = 4T$.
4. Das Ergebnis der grafischen Faltung für die Zeitpunkte $t = 2T$ und $3T$ kann man nachfolgender Skizze entnehmen. Der Wert bei $2T$ entspricht der rötlich unterlegten Fläche:
$$y_2( {t = 2T} ) = \frac{1}{2}\cdot ( {\frac{1}{T} + \frac{1}[[:Vorlage:2T]]} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.75 {\rm V}} .$$
Die grün unterlegte Fläche kennzeichnet den Wert bei $3T$:
$$y_2( {t = 3T} ) = \frac{1}{2}\cdot ( {\frac{1}{2T} + 0} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.25 {\rm V}} .$$
Um den gesamten Signalverlauf zwischen $T$ und $4T$ zu berechnen, müssen drei Bereiche getrennt betrachtet werden. Zur Vereinfachung der Darstellung wird im Folgenden $x_0 = 1$ gesetzt.
Im Bereich $T \leq t \leq 2T$ liegt die untere Integrationsgrenze fest bei $τ_u = 0$ und die obere Grenze bei $τ_0 = t – T$:
$$y_2 (t) = \int_{\tau _u }^{\tau _0 } {h(\tau )\,{\rm{d}}\tau = \int_0^{t - T} {\frac{1}{T}} }\cdot \left( {1 - \frac{\tau }[[:Vorlage:2T]]} \right)\,{\rm{d}}\tau .$$
Mit dem unbestimmten Integral
$$I(\tau ) = \frac{\tau }{T} - 0.25 \cdot \left( {\frac{\tau }{T}} \right)^2$$
ergibt sich
$$y_2 (t) = I(t - T) - I(0) = \frac[[:Vorlage:T - T]]{T} - 0.25 \cdot \left( {\frac[[:Vorlage:T - T]]{T}} \right)^2 $$
$$ \Rightarrow \;y_2 (t) = 1.5 \cdot \frac{t}{T} - 0.25\cdot \left( {\frac{t}{T}} \right)^2 - 1.25.$$
Zur Verifizierung betrachten wir die beiden Grenzen. Man erhält die bereits oben berechneten Werte $y_2(T) = 0$ und $y_2(2T) = 0.75$.
Im Intervall $2T \leq t \leq 3T$ liegt die obere Integrationsgrenze weiterhin bei $τ_0 = t – T$, während nun $τ_u = t – 2T$ gilt:
$$y_2 (t) = I(t - T) - I(t - 2T) = 1.75 - 0.5 \cdot \frac{t}{T}.$$
Dies entspricht einem linearen Abfall mit den zwei Grenzwerten $y_2(2T) = 0.75$ und $y_2(3T) = 0.25$.
Schließlich liegt im Intervall $3T \leq t \leq 4T$ die obere Grenze fest bei $τ_0 = 2T$ und es gilt weiterhin $τ_u = t – 2T$:
$$\begin{align*}y_2 (t) &= I(2T) - I(t - 2T) \\ &= - 2 \cdot \frac{t}{T} + 0.25\left( {\frac{t}{T}} \right)^2 + 4.\end{align*}$$
Auch hier ergeben sich die richtigen Grenzwerte
$$y_2 (3T) = 0.25\quad {\rm{und}}\quad y_2 (4T) = 0.$$
5. Auch diese Aufgabe könnte direkt mit der Faltung gelöst werden. Da $x_3(t)$ eine gerade Funktion ist, kann hier aber nun auf die Spiegelung verzichtet werden und man erhält
$$y_3 (t) = \int_{ - \infty }^{ + \infty } {h(\tau ) \cdot x_3 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau = x_0 }\cdot \int_0^{2T} {h(\tau ) \cdot \cos (2{\rm{\pi }}f_0 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau .}$$
Einfacher ist hier der Weg über die Spektren. $X(f)$ besteht aus zwei Diraclinien bei $\pm 3f_0$. Somit muss auch nur für diese Frequenz der Frequenzgang berechnet werden:
$$\begin{align*}H( {f = 3f_0 } ) & = \frac{1}{{72{\rm{\pi }}^{\rm{2}} }}\left[ {1 - {\rm{j}}\cdot 12{\rm{\pi }} - {\rm{cos}}( {{\rm{12\pi }}} ) + {\rm{j}}\cdot \sin ( {{\rm{12\pi }}})} \right] = \\ & = \frac{1}{{72{\rm{\pi }}^{\rm{2}} }}\left[ 1 - {\rm j}\cdot 12{\rm \pi } - 1 + {\rm j}\cdot 0 \right]= { - {\rm{j}}} \cdot \frac{1}{{6{\rm{\pi }}}}.\end{align*}$$
Somit lautet das Spektrum des Ausgangssignals:
$$Y(f) = - {\rm{j}} \cdot \frac[[:Vorlage:X 0]]{{{\rm{12\pi }}}}\cdot \delta \left( {f - 3f_0 } \right) + {\rm{j}} \cdot \frac[[:Vorlage:X 0]]{{{\rm{12\pi }}}}\cdot \delta \left( {f + 3f_0 } \right).$$
Das Signal $y_3(t)$ ist somit sinusförmig mit der Amplitude $x_0/(6\pi )$. Der Signalwert bei $t$ = 0 ist 0.