Aufgaben:Aufgabe 3.9: Faltung von Rechteck und Gauß

• Zurück zum Buch

Wir betrachten in der Aufgabe einen gaußförmigen Tiefpass mit der äquivalenten Bandbreite $\Delta f$ = 40 MHz:

$$H( f ) = {\rm{e}}^{{\rm{ - \pi }}( {f/\Delta f} )^2 } .$$

Die dazugehörige Impulsantwort lautet:

$$h( t ) = \Delta f \cdot {\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm} \cdot \hspace{0.05cm} t} )^2 } .$$

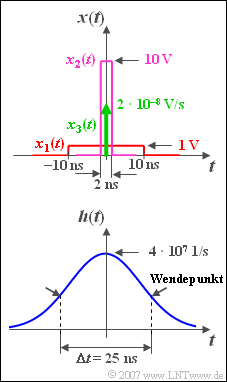
Aus der Skizze ist zu ersehen, dass die äquivalente Zeitdauer der Impulsantwort $h(t)$ ⇒ $\Delta t = 1/\Delta f = 25$ ns an den beiden Wendepunkten der Gaußfunktion abgelesen werden kann. An den Eingang des Tiefpasses werden nun drei verschiedene impulsartige Signale angelegt:

• ein Rechteckimpuls $x_1(t)$ mit der Amplitude 1 V und der Dauer $T_1$ = 20 ns (roter Kurvenverlauf),
• ein Rechteckimpuls $x_2(t)$ mit der Amplitude $A_2$ = 10 V und der Dauer $T_2$ = 2 ns (violetter Kurvenverlauf),
• ein Diracimpuls $x_3(t)$ mit dem Impulsgewicht $2 \cdot 10^{–8}$ Vs (grüner Pfeil).

Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.4. Zur Lösung der nachfolgenden Fragen können Sie das komplementäre Gaußsche Fehlerintegral benutzen, das wie folgt definiert ist (siehe Kapitel 3.5 im Buch „Stochastische Signale”):

$$\rm{Q}( x ) = \frac{1}{ {\sqrt {2{\rm{\pi }}} }}\int_{\it x}^\infty {{\rm{e}}^{{{ - {\it u}}}^{\rm{2}} {\rm{/2}}} }\hspace{0.1cm}{\rm{d}}{\it u}.$$

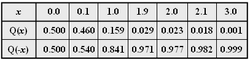
Die nachfolgende Tabelle gibt einige Funktionswerte wieder:

Fragebogen

1

Berechnen Sie das Signal $y_1(t) = x_1(t) \ast h(t)$. Welche Werte ergeben sich zu den Zeiten $t$ = 0 und $t$ = 20 ns mit der Näherung $(2\pi )1/2 \approx 2.5$?

$y_1(t=0) =$ V

$y_1(t=20\text{ns}) =$ V

2

Welche Signalwerte ergeben sich beim Ausgangssignal $y_2(t) = x_2(t) \ast h(t)$ zu den Zeitpunkten $t$ = 0 und $t$ = 20 ns?

$y_2(t=0) =$ V

$y_2(t=20\text{ns}) =$ V

3

Wie groß ist das Ausgangssignal $y_3(t) = x_3(t) \ast h(t)$ zu den betrachteten Zeitpunkten? Interpretieren Sie das Ergebnis.

$y_3(t=0) =$ V

$y_3(t=20\text{ns}) =$ V

Musterlösung

Musterlösung

1. Das Faltungsintegral lautet hier:

$$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{ {A_1 }}{ {\sqrt {2{\rm{\pi }}} }}\int_{u_1 }^{u_2 } {{\rm{e}}^{[[:Vorlage:- u]]^{\rm{2}}{\rm{/2}}}\hspace{0.1cm} {\rm{d}}u.}$$

Hierbei wurde die folgende Substitution verwendet:

$$u = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \tau$$

Die Integrationsgrenzen liegen bei:

$$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \left( {t - T_1 /2} \right),$$

$$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \left( {t + T_1 /2} \right).$$

Mit dem komplementären Gaußschen Fehlerintegral kann hierfür auch geschrieben werden:

$$y_1 (t) = A_1 \cdot \left[ {{\rm Q} ( {u_1 } ) - {\rm Q}( {u_2 } )} \right].$$

Für den Zeitpunkt $t = 0$ erhält man mit $(2\pi )1/2 \approx 2.5$:

$$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$

Mit $u_1 = –u_2 = –1$ folgt weiter:

$$y_1 ( {t = 0} ) \approx A_1 \cdot \left[ {{\rm Q}( { - 1} ) - {\rm Q}(+ 1 )} \right] = 1\;{\rm{V}} \cdot \left[ {{\rm{0}}{\rm{.841 - 0}}{\rm{.159}}} \right] \hspace{0.15 cm}\underline{= 0.682\;{\rm{V}}}{\rm{.}}$$

Für den zweiten Zeitpunkt erhält man entsprechend:

$$y_1 ( {t = 20\;{\rm{ns}}} ) \approx A_1 \cdot \left[ {{\rm Q}( 1 ) - {\rm Q}( 3 )} \right] = 1\;{\rm{V}} \cdot \left[ {{\rm{0}}{\rm{.159 - 0}}{\rm{.001}}} \right] \hspace{0.15 cm}\underline{= 0.158\;{\rm{V}}}{\rm{.}}$$

2. Analog zur obigen Musterlösung kann nun geschrieben werden:

$$y_2 ( {t = 0} ) \approx A_2 \cdot \left[ {{\rm Q}( { - 0.1} ) - {\rm Q}( {0.1} )} \right] = 10\;{\rm{V}} \cdot \left[ {{\rm{0}}{\rm{.540 - 0}}{\rm{.460}}} \right] \hspace{0.15 cm}\underline{= 0.80\;{\rm{V}}}{\rm{,}}$$

$$y_2 ( {t = 20\,{\rm ns}} ) \approx A_2 \cdot \left[ {{\rm Q}( {1.9} ) - {\rm Q}( {2.1} )} \right] = 10\;{\rm{V}} \cdot \left[ {{\rm{0}}{\rm{.029 - 0}}{\rm{.018}}} \right] \hspace{0.15 cm}\underline{= 0.11\;{\rm{V}}}{\rm{.}}$$

3. Beim diracförmigen Eingangssignal $x_3(t)$ ist das Ausgangssignal $y_3(t)$ gleich der Impulsantwort $h(t)$, gewichtet mit dem Gewicht der Diracfunktion:

$$y_3 (t) = 2 \cdot 10^{ - 8} \,{\rm{Vs}} \cdot 4 \cdot 10^7 \;{\rm{1/s}} \cdot {\rm{e}}^{ - {\rm{\pi }}( {\Delta f \cdot t})^2 }.$$

Zum Zeitpunkt $t$ = 0 erhält man 0.8 V. Nach $t$ = 20 Nanosekunden ist der Ausgangsimpuls um den Faktor exp(–0.64π) ≈ 0.136 kleiner und man erhält das Ergebnis $y_3$( $t$ = 20 ns) ≈ 0.11 V. Man erkennt aus dem Vergleich der Resultate aus 2) und 3), dass $y_3(t)$ ≈ $y_2(t)$ gilt. Der Grund hierfür ist, dass der Diracimpuls eine gute Näherung für einen rechteckförmigen Eingangsimpuls gleicher Fläche ist, wenn die Rechteckdauer $T$ deutlich kleiner ist als die äquivalente Impulsdauer $\Delta t$ der Impulsantwort. Das heißt für unser Beispiel: Für $T$ << $\Delta t$ ist auch der Ausgangsimpuls nahezu gaußförmig.