Lineare zeitinvariante Systeme/Systembeschreibung im Frequenzbereich: Unterschied zwischen den Versionen
| Zeile 21: | Zeile 21: | ||
Anmerkung: Das System kann im Allgemeinen von beliebiger Art sein und ist nicht allein auf die Nachrichtentechnik beschränkt. Vielmehr wird auch in anderen Wissenschaftsgebieten wie zum Beispiel den Naturwissenschaften, der Volks- und Betriebswirtschaft, der Soziologie und Politologie versucht, Kausalzusammenhänge zwischen verschiedenen Größen durch das Ursachen–Wirkungs–Prinzip zu erfassen und zu beschreiben. Die für diese phänomenologischen Systemtheorien angewandten Methoden unterscheiden sich aber deutlich von der Vorgehensweise in der Nachrichtentechnik, die in diesem ersten Kapitel des Buches „Lineare zeitinvariante Systeme” dargelegt wird. | Anmerkung: Das System kann im Allgemeinen von beliebiger Art sein und ist nicht allein auf die Nachrichtentechnik beschränkt. Vielmehr wird auch in anderen Wissenschaftsgebieten wie zum Beispiel den Naturwissenschaften, der Volks- und Betriebswirtschaft, der Soziologie und Politologie versucht, Kausalzusammenhänge zwischen verschiedenen Größen durch das Ursachen–Wirkungs–Prinzip zu erfassen und zu beschreiben. Die für diese phänomenologischen Systemtheorien angewandten Methoden unterscheiden sich aber deutlich von der Vorgehensweise in der Nachrichtentechnik, die in diesem ersten Kapitel des Buches „Lineare zeitinvariante Systeme” dargelegt wird. | ||
| − | |||
==Anwendung in der Nachrichtentechnik== | ==Anwendung in der Nachrichtentechnik== | ||
| − | |||
| − | |||
Das Ursachen–Wirkungs–Prinzip lässt sich auch in der Nachrichtentechnik anwenden, beispielsweise zur Beschreibung von Zweipolen. Hier kann man den Stromverlauf "i(t)" als Ursachen- und die Spannung "u(t)" als Wirkungsfunktion betrachten. Durch Beobachten der I/U–Beziehungen lassen sich so Rückschlüsse über die Eigenschaften des eigentlich unbekannten Zweipols ziehen. | Das Ursachen–Wirkungs–Prinzip lässt sich auch in der Nachrichtentechnik anwenden, beispielsweise zur Beschreibung von Zweipolen. Hier kann man den Stromverlauf "i(t)" als Ursachen- und die Spannung "u(t)" als Wirkungsfunktion betrachten. Durch Beobachten der I/U–Beziehungen lassen sich so Rückschlüsse über die Eigenschaften des eigentlich unbekannten Zweipols ziehen. | ||
| − | |||
| − | |||
Karl Küpfmüller hat den Begriff „Systemtheorie” 1949 erstmals (in Deutschland) eingeführt. Er versteht darunter eine Methode zur Beschreibung komplexer Kausalzusammenhänge in Naturwissenschaften und Technik, basierend auf einer Spektraltransformation – beispielsweise der im Buch „Signaldarstellung” dargelegten Fouriertransformation. | Karl Küpfmüller hat den Begriff „Systemtheorie” 1949 erstmals (in Deutschland) eingeführt. Er versteht darunter eine Methode zur Beschreibung komplexer Kausalzusammenhänge in Naturwissenschaften und Technik, basierend auf einer Spektraltransformation – beispielsweise der im Buch „Signaldarstellung” dargelegten Fouriertransformation. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Man kann ein ganzes Nachrichtensystem systemtheoretisch beschreiben. Hier ist die Ursachenfunktion das Eingangssignal "x(t)" bzw. dessen Spektrum "X(f)" und die Wirkungsfunktion das Ausgangssignal "y(t)" oder die dazugehörige Spektralfunktion "Y(f)". | Man kann ein ganzes Nachrichtensystem systemtheoretisch beschreiben. Hier ist die Ursachenfunktion das Eingangssignal "x(t)" bzw. dessen Spektrum "X(f)" und die Wirkungsfunktion das Ausgangssignal "y(t)" oder die dazugehörige Spektralfunktion "Y(f)". | ||
Version vom 29. April 2016, 14:53 Uhr
Das Ursachen-Wirkungs-Prinzip
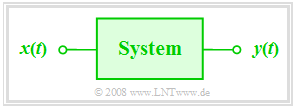
Wir betrachten in diesem Kapitel stets das folgende einfache Modell:
Diese Anordnung ist wie folgt zu interpretieren:
- Im Mittelpunkt steht das so genannte System, das in seiner Funktion weitestgehend abstrahiert ist („Black Box”). Über die Realisierung des Systems ist nichts Genaues bekannt.
- Die auf dieses System einwirkende zeitabhängige Eingangsgröße x(t) bezeichnen wir im Folgenden auch als die Ursachenfunktion.
- Am Ausgang des Systems erscheint dann die Wirkungsfunktion y(t) – quasi als Antwort des Systems auf die Eingangsfunktion x(t).
Anmerkung: Das System kann im Allgemeinen von beliebiger Art sein und ist nicht allein auf die Nachrichtentechnik beschränkt. Vielmehr wird auch in anderen Wissenschaftsgebieten wie zum Beispiel den Naturwissenschaften, der Volks- und Betriebswirtschaft, der Soziologie und Politologie versucht, Kausalzusammenhänge zwischen verschiedenen Größen durch das Ursachen–Wirkungs–Prinzip zu erfassen und zu beschreiben. Die für diese phänomenologischen Systemtheorien angewandten Methoden unterscheiden sich aber deutlich von der Vorgehensweise in der Nachrichtentechnik, die in diesem ersten Kapitel des Buches „Lineare zeitinvariante Systeme” dargelegt wird.
Anwendung in der Nachrichtentechnik
Das Ursachen–Wirkungs–Prinzip lässt sich auch in der Nachrichtentechnik anwenden, beispielsweise zur Beschreibung von Zweipolen. Hier kann man den Stromverlauf "i(t)" als Ursachen- und die Spannung "u(t)" als Wirkungsfunktion betrachten. Durch Beobachten der I/U–Beziehungen lassen sich so Rückschlüsse über die Eigenschaften des eigentlich unbekannten Zweipols ziehen.
Karl Küpfmüller hat den Begriff „Systemtheorie” 1949 erstmals (in Deutschland) eingeführt. Er versteht darunter eine Methode zur Beschreibung komplexer Kausalzusammenhänge in Naturwissenschaften und Technik, basierend auf einer Spektraltransformation – beispielsweise der im Buch „Signaldarstellung” dargelegten Fouriertransformation.
Man kann ein ganzes Nachrichtensystem systemtheoretisch beschreiben. Hier ist die Ursachenfunktion das Eingangssignal "x(t)" bzw. dessen Spektrum "X(f)" und die Wirkungsfunktion das Ausgangssignal "y(t)" oder die dazugehörige Spektralfunktion "Y(f)".