Lineare zeitinvariante Systeme/Lineare Verzerrungen: Unterschied zwischen den Versionen
| Zeile 143: | Zeile 143: | ||
*Gilt bei einem System $b(ω) = τ_P · ω$ bzw. $b(f) = 2π · τ_P · f$, so haben alle Frequenzen die gleiche Phasenlaufzeit $τ_P$. Ein solches System führt nicht zu Phasenverzerrungen. | *Gilt bei einem System $b(ω) = τ_P · ω$ bzw. $b(f) = 2π · τ_P · f$, so haben alle Frequenzen die gleiche Phasenlaufzeit $τ_P$. Ein solches System führt nicht zu Phasenverzerrungen. | ||
| + | ==Unterschied zwischen Phasen- und Gruppenlaufzeit== | ||
| + | Eine weitere wichtige Systembeschreibungsgröße die so genannte Gruppenlaufzeit, die nicht mit der Phasenlaufzeit verwechselt werden sollte. Die Gruppenlaufzeit ist wie folgt definiert: | ||
| + | $$\tau_{\rm G}(\omega_0) = \left[ \frac{{\rm d}b(\omega)}{{\rm d}\omega}\right ]_{\omega = \omega_0}.$$ | ||
| + | Diese Größe wird vorwiegend zur Beschreibung von Schmalbandsystemen herangezogen. Sie gibt die Verzögerung an, welche die Hüllkurve eines Bandpass-Systems erfährt. | ||
| + | {{Beispiel}} | ||
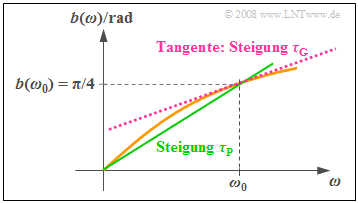
| + | Beispiel: Die Grafik zeigt die Phasenfunktion $b(ω) = arctan (ω/ω_0)$, die monoton von 0 (bei $ω =$ 0) bis $π/2$ (für $ω → ∞$) ansteigt. Der Funktionswert bei $ω = ω_0$ beträgt $π/4$. | ||
| + | |||
| + | [[Datei: P_ID904__LZI_T_2_3_S5_neu.png |400px | Zur Definition der Gruppenlaufzeit]] | ||
| + | |||
| + | Setzen wir $ω_0 = 2π · 1$ kHz, so erhalten wir für die Phasenlaufzeit: | ||
| + | $$\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}= \frac{\pi / 4}{2 \pi \cdot{1\, \rm kHz}} = {125\, \rm \mu s}.$$ | ||
| + | Diese Größe entspricht der Steigung der grün eingezeichneten Geraden in der obigen Grafik. Dagegen kennzeichnet die geringere Steigung der rot dargestellten Tangente die ''Gruppenlaufzeit:'' | ||
| + | $$\tau_{\rm G}(\omega_0) = \left[ \frac{{\rm d}b(\omega)}{{\rm d}\omega}\right ]_{\omega = \omega_0} = | ||
| + | \left[ \frac{1}{\omega_0} \cdot \frac{1}{1 + \left(\omega / \omega_0\right]^2} \right ]_{\omega = | ||
| + | \omega_0} | ||
| + | = \frac{1}{2\omega_0}= \frac{1}{4 \pi \cdot{1\, \rm kHz}} | ||
| + | \approx {80\, \rm \mu s}.$$ | ||
Version vom 7. Mai 2016, 11:42 Uhr
Inhaltsverzeichnis
Zusammenstellung wichtiger Beschreibungsgrößen
Für diesen Abschnitt 2.3 werden nichtlineare Verzerrungen ausgeschlossen, so dass das System durch den Frequenzgang $H(f)$ vollständig beschrieben wird:
Der im Allgemeinen komplexe Frequenzgang kann auch wie folgt dargestellt werden: $$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
Daraus ergeben sich folgende Beschreibungsgrößen:
- Der Betrag $|H(f)|$ wird als Amplitudengang und in logarithmierter Form als Dämpfungsverlauf bezeichnet:
$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Dezibel \hspace{0.1cm}(dB) }.$$
- Der Phasengang $b(f)$ gibt den negativen frequenzabhängigen Winkel von $H(f)$ in der komplexen Ebene an, bezogen auf die reelle Achse:
$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$
Dämpfungs- und Phasenverlauf bei verzerrungsfreien Systemen (1)
Nach den Ausführungen im Kapitel 2.1 liegt genau dann ein verzerrungsfreies System vor, wenn alle Frequenzanteile gleichermäßig gedämpft und verzögert werden: $$y(t) = \alpha \cdot x(t - \tau).$$ Nach den Gesetzmäßigkeiten der Systemtheorie muss deshalb für den Frequenzgang $$H(f) = \alpha \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f \tau}$$ gelten, oder ausgedrückt mit den Funktionen $a(f)$ und $b(f)$:
- Der Dämpfungsverlauf muss für alle im Eingangssignal enthaltenen Frequenzen konstant sein:
$$a(f) = - \ln |H(f)| = - \ln \alpha = {\rm const.}$$
- Der Phasenverlauf muss im interessierenden Bereich entweder 0 sein (System ohne Laufzeit) oder linear mit der Frequenz ansteigen $(τ$ gibt dabei die Laufzeit an):
$$b(f) = 2 \pi f \tau = {\rm const.} \cdot f.$$
Bei einem verzerrungsfreien System müssen beide Forderungen gleichzeitig erfüllt sein. Bei Verletzung auch nur einer dieser beiden Bedingungen kommt es zu linearen Verzerrungen, die entsprechend ihrer Ursache unterschieden werden.
Dämpfungsverzerrungen gibt es, wenn im interessierenden Frequenzbereich der Dämpfungsverlauf nicht konstant ist: $$a(f) \ne {\rm const.}$$ Phasenverzerrungen liegen vor, wenn die Phasenfunktion nicht linear bezüglich $f$ ist: $$b(f) \ne {\rm const.} \cdot f.$$
Anzumerken ist, dass bei allen realisierbaren Systemen – insbesondere den im Kapitel 3 beschriebenen „minimalphasigen” – meist beide Verzerrungsformen gleichzeitig auftreten.
Im Zeitbereich lautet die Bedingung für ein verzerrungsfreies System: $$h(t) = \alpha \cdot \delta(t - \tau),\hspace{0.4cm}\alpha \ne 0.$$
Ist zudem $α =$ 1 und $τ =$ 0, so liegt ein ideales Übertragungssystem vor. Dagegen gibt es immer dann lineare Verzerrungen, wenn
- $h(t)$ eine zeitkontinuierliche Funktion ist, oder
- $h(t)$ sich aus mehr als einer Diracfunktion zusammensetzt.
Dämpfungs- und Phasenverlauf bei verzerrungsfreien Systemen (2)
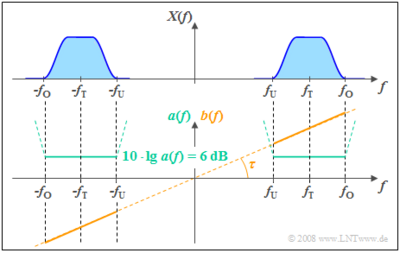
Beispiel: Das nachfolgende Bild zeigt den Dämpfungsverlauf $a(f)$ und den Phasenverlauf $b(f)$ eines verzerrungsfreien Systems. In einem Bereich von $f_U$ bis $f_O$ um die Trägerfrequenz $f_T$, in dem das Signal $x(t)$ Anteile besitzt, ist $a(f)$ konstant. Aus dem angegebenen konstanten Dämpfungswert 6 dB folgt für den Amplitudengang $|H(f)| =$ 0.5. Das Ausgangsspektrum $Y(f)$ ist somit betragsmäßig halb so groß wie die Spektralanteile $X(f)$ des Eingangssignals.
Der Phasenverlauf $b(f)$ steigt zwischen $f_U$ und $f_O$ linear mit der Frequenz an. Dies hat zur Folge, dass alle Frequenzanteile um die gleiche Phasenlaufzeit $τ$ verzögert werden, wobei $τ$ durch die Steigung von $b(f)$ festliegt. Mit $b(f) =$ 0 würde sich ein laufzeitfreies System $(τ =$ 0) ergeben.
Weiter sind aus der Grafik die allgemeingültigen Eigenschaften zu erkennen:
- Der Dämpfungsverlauf $a(f) = a(– f)$ ist eine gerade Funktion in $f$.
- Der Phasenverlauf $b(f) = – b(–f)$ ist eine ungerade Funktion in $f$.
Außerhalb des durch $x(t)$ belegten Frequenzbandes müssen die Bedingungen „konstante Dämpfung” und „lineare Phase” nicht eingehalten werden. Man erkennt aus dem gestrichelt eingezeichneten Verlauf von $a(f)$, dass hier sogar eine sehr viel höhere Dämpfung zweckmäßig ist, da dadurch die stets vorhandenen – in diesem Buch aber nicht betrachteten – Rauschanteile außerhalb der Nutzbandbreite besser unterdrückt werden.
Dämpfungsverzerrungen
Wir betrachten im Folgenden als Eingangssignal die Summe zweier harmonischer Schwingungen: $$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - \varphi_2).$$
Ist dann das Ausgangssignal in der Form $$y(t) = \alpha_1 \cdot A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + \alpha_2 \cdot A_2 \cdot \cos(2 \pi f_2 \cdot t - \varphi_2).$$ darstellbar und gilt gleichzeitig $α_1 ≠ α_2$, so liegen ausschließlich Dämpfungsverzerrungen vor
Die Dämpfungskonstanten $α_1$ und $α_2$ können aus dem Amplitudengang $|H(f)|$ ermittelt werden: $$\alpha_1 = |H(f_1)|,\hspace{0.4cm}\alpha_2 = |H(f_2)|.$$
Ist der Dämpfungsverlauf $a(f)$ in Neper gegeben, so gilt gleichermaßen (1 dB entspricht 0.1155 Np): $$ \alpha_1 = {\rm e}^{-{\rm a}(f_1)},\hspace{0.4cm}\alpha_2 = {\rm e}^{-{\rm a}(f_2)}.$$
Bitte beachten Sie: Bei manchen Zeichenfonts sind „a” von $„α”$ (alpha) schwer zu unterscheiden.
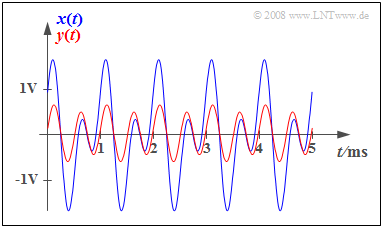
Beispiel: Die Grafik zeigt das mit $T_0 =$ 1 ms periodische Eingangssignal (blauer Verlauf) $$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$ sowie das mit $α_1 =$ 0.2 und $α_2 =$ 0.5 dämpfungsverzerrte Signal $y(t)$. Man erkennt die signifikanten Auswirkungen dieser Dämpfungsverzerrungen: $y(t)$ hat nur noch wenig Ähnlichkeit mit $x(t)$. Mit $α_1 = α_2 = α$ würde sich dagegen das verzerrungsfreie Signal $y(t) = α · x(t)$ ergeben, aus dem durch Verstärkung um 1/ $α$ das ursprüngliche Signal $x(t)$ wieder hergestellt werden könnte.
Mit dem folgenden Berechnungstool können unter Anderem Dämpfungsverzerrungen visualisiert werden.
Nähere Informationen finden Sie in der Animation selbst unter dem Menüpunkt „Erläuterung”.
Phasenlaufzeit
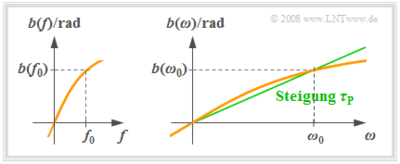
Wir betrachten ein System mit $|H(f)| =$ 1, so dass für den Frequenzgang gilt: $$H(f) = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ Die Grafik zeigt einen beispielhaften Phasenverlauf $b(f)$. Zu beachten ist, dass der Phasenverlauf eine ungerade Funktion bezüglich der Frequenz $f$ ist: $b(–f) = –b(f)$. Rechts ist die Funktion $b(ω)$ skizziert, die gegenüber $b(f)$ in der Abszisse um den Faktor $2π$ gestreckt ist.
Liegt am Eingang die harmonische Schwingung $$x(t) = C \cdot \cos(2 \pi f_0 t - \varphi) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f ) = \frac{C}{2}\cdot {\rm e}^{{\rm j}\hspace{0.01cm} \varphi} \cdot \delta(f + f_0) \hspace{0.01cm} + \hspace{0.01cm}\frac{C}{2}\cdot {\rm e}^{-{\rm j}\hspace{0.01cm} \varphi} \cdot \delta(f - f_0)$$ an, so ergibt sich für die Spektralfunktion am Ausgang $$Y(f ) = \frac{C}{2}\cdot {\rm e}^{{\rm j}\hspace{0.05cm} \varphi} \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm} b(f_0)} \cdot \delta(f + f_0) \hspace{0.05cm} + \hspace{0.05cm}\frac{C}{2}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \varphi}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} b(f_0)} \cdot \delta(f - f_0).$$ Somit lautet das Ausgangssignal: $$y(t) = C \cdot \cos(2 \pi f_0 t - b(f_0) - \varphi).$$ Dieses kann auch in folgender Form dargestellt werden: $$y(t) = C \cdot \cos(2 \pi f_0 ( t - \tau_{\rm P}(f_0)) - \varphi).$$
Definition: Die Phasenlaufzeit gibt die Verzögerung an, die eine harmonische Schwingung mit der Frequenz $f_0$ durch das System erfährt; sie ist bei phasenverzerrenden Systemen frequenzabhängig: $$\tau_{\rm P}(f_0) = \frac{b(f_0)}{2\pi f_0} \hspace{0.4cm}{\rm bzw.} \hspace{0.4cm} \tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}.$$
Hierzu ist Folgendes anzumerken:
- In der $b(ω)$–Darstellung kann die Phasenlaufzeit $τ_P$ als die Steigung der grün eingezeichneten Geraden auch grafisch ermittelt werden.
- Im Allgemeinen wird eine Schwingung mit anderer Frequenz auch eine andere Phasenlaufzeit zur Folge haben. Dies ist der physikalische Hintergrund für Phasenverzerrungen.
- Gilt bei einem System $b(ω) = τ_P · ω$ bzw. $b(f) = 2π · τ_P · f$, so haben alle Frequenzen die gleiche Phasenlaufzeit $τ_P$. Ein solches System führt nicht zu Phasenverzerrungen.
Unterschied zwischen Phasen- und Gruppenlaufzeit
Eine weitere wichtige Systembeschreibungsgröße die so genannte Gruppenlaufzeit, die nicht mit der Phasenlaufzeit verwechselt werden sollte. Die Gruppenlaufzeit ist wie folgt definiert: $$\tau_{\rm G}(\omega_0) = \left[ \frac{{\rm d}b(\omega)}{{\rm d}\omega}\right ]_{\omega = \omega_0}.$$ Diese Größe wird vorwiegend zur Beschreibung von Schmalbandsystemen herangezogen. Sie gibt die Verzögerung an, welche die Hüllkurve eines Bandpass-Systems erfährt.
Beispiel: Die Grafik zeigt die Phasenfunktion $b(ω) = arctan (ω/ω_0)$, die monoton von 0 (bei $ω =$ 0) bis $π/2$ (für $ω → ∞$) ansteigt. Der Funktionswert bei $ω = ω_0$ beträgt $π/4$.
Setzen wir $ω_0 = 2π · 1$ kHz, so erhalten wir für die Phasenlaufzeit: $$\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}= \frac{\pi / 4}{2 \pi \cdot{1\, \rm kHz}} = {125\, \rm \mu s}.$$ Diese Größe entspricht der Steigung der grün eingezeichneten Geraden in der obigen Grafik. Dagegen kennzeichnet die geringere Steigung der rot dargestellten Tangente die Gruppenlaufzeit: $$\tau_{\rm G}(\omega_0) = \left[ \frac{{\rm d}b(\omega)}{{\rm d}\omega}\right ]_{\omega = \omega_0} = \left[ \frac{1}{\omega_0} \cdot \frac{1}{1 + \left(\omega / \omega_0\right]^2} \right ]_{\omega = \omega_0} = \frac{1}{2\omega_0}= \frac{1}{4 \pi \cdot{1\, \rm kHz}} \approx {80\, \rm \mu s}.$$