Aufgaben:Aufgabe 1.7Z: Systemanalyse: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige systemtheoretische Tiefpassfunktionen}} [[Datei:|right|]] ===Fragebogen=== <quiz display=simp…“) |
|||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige systemtheoretische Tiefpassfunktionen}} | {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige systemtheoretische Tiefpassfunktionen}} | ||
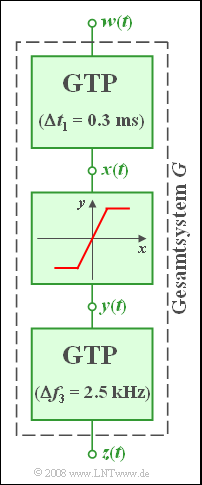
| − | [[Datei:|right|]] | + | [[Datei:P_ID865__LZI_Z_1_7.png|right|System mit Gaußtiefpässen und nichtlinearer Kennlinie (Aufgabe Z1.7)]] Ein Gesamtsystem $G$ mit Eingang $w(t)$ und Ausgang $z(t)$ besteht aus drei Komponenten: |
| + | *Die erste Komponente ist ein Gaußtiefpass mit Impulsantwort | ||
| + | $$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi(t/\Delta t_1)^2}, \hspace{0.5cm} \Delta | ||
| + | t_1= {0.3\,\rm ms}.$$ | ||
| + | *Danach folgt eine Nichtlinearität mit Kennlinie | ||
| + | $$y(t) = \left\{ \begin{array}{c} {8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge {4\,\rm V}}, \\ | ||
| + | {{-4\,\rm V} < x(t) < {4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$ | ||
| + | :Deren Eingangssignal $x(t)$ wird um den Faktor 2 verstärkt und – falls nötig – auf den Amplitudenbereich ±8V begrenzt. | ||
| + | *Am Ende der Kette folgt wieder ein Gaußtiefpass, der durch seinen Frequenzgang gegeben ist: | ||
| + | $$H_3(f) = {\rm e}^{-\pi(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$ | ||
| + | |||
| + | |||
| + | Das Eingangssignal $w(t)$ sei ein Gaußimpuls mit konstanter Amplitude 5 V, aber variabler Breite $T$: | ||
| + | $$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi(t/T)^2}.$$ | ||
| + | Zu untersuchen ist, in welchem Bereich die äquivalente Impulsdauer $T$ dieses Gaußimpulses variieren kann, damit das Gesamtsystem durch den Frequenzband | ||
| + | $$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi(f/\Delta f_{\rm G})^2}$$ | ||
| + | vollständig beschrieben wird. Der Index „G” bei Frequenzgang und Bandbreite bezieht sich jeweils auf „Gesamtsystem”. | ||
| + | |||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf den Abschnitt [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen#Gau.C3.9F.E2.80.93Tiefpass|Gaußtiefpass]] im Kapitel 1.3. | ||
Version vom 5. August 2016, 16:46 Uhr
Ein Gesamtsystem $G$ mit Eingang $w(t)$ und Ausgang $z(t)$ besteht aus drei Komponenten:
- Die erste Komponente ist ein Gaußtiefpass mit Impulsantwort
$$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi(t/\Delta t_1)^2}, \hspace{0.5cm} \Delta t_1= {0.3\,\rm ms}.$$
- Danach folgt eine Nichtlinearität mit Kennlinie
$$y(t) = \left\{ \begin{array}{c} {8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge {4\,\rm V}}, \\ {{-4\,\rm V} < x(t) < {4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$
- Deren Eingangssignal $x(t)$ wird um den Faktor 2 verstärkt und – falls nötig – auf den Amplitudenbereich ±8V begrenzt.
- Am Ende der Kette folgt wieder ein Gaußtiefpass, der durch seinen Frequenzgang gegeben ist:
$$H_3(f) = {\rm e}^{-\pi(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$
Das Eingangssignal $w(t)$ sei ein Gaußimpuls mit konstanter Amplitude 5 V, aber variabler Breite $T$:
$$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi(t/T)^2}.$$
Zu untersuchen ist, in welchem Bereich die äquivalente Impulsdauer $T$ dieses Gaußimpulses variieren kann, damit das Gesamtsystem durch den Frequenzband
$$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi(f/\Delta f_{\rm G})^2}$$
vollständig beschrieben wird. Der Index „G” bei Frequenzgang und Bandbreite bezieht sich jeweils auf „Gesamtsystem”.
Hinweis: Die Aufgabe bezieht sich auf den Abschnitt Gaußtiefpass im Kapitel 1.3.
Fragebogen
Musterlösung
- a)
- b)
- c)
- d)
- e)
- f)
- g)