Aufgaben:Aufgabe 2.3Z: Zur LZ77-Codierung

• Zurück zum Buch

In der Aufgabe A2.3 sollten Sie BARBARA–BAR (String der Länge 11, vier verschiedene Zeichen) mit dem LZ78–Algorithmus komprimieren. In dieser Aufgabe verwenden wir den gleichen Text zur Demonstration der LZ77–Komprimierung.

Anzumerken ist:

• Während beim Nachfolger LZ78 sukzessive ein globales Wörterbuch aufgebaut wird, verwendet LZ77 ein lokales Wörterbuch.

• Das LZ77–Verfahren arbeitet mit einem Sliding Window, das schrittweise über den Eingabetext verschoben wird.

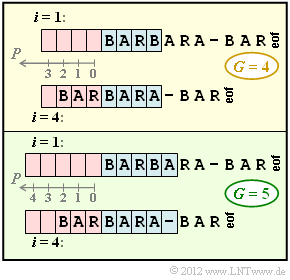
• Dieses „gleitende Fenster” ist unterteilt in den Vorschaupuffer (in der Grafik blau hinterlegt) und den Suchpuffer (rote Hinterlegung). Beide Puffer haben eine Größe von G Speicherplätzen.

• Jeder Codierschritt i wird durch ein Zahlentriple (P, L, Z) charakterisiert. Hierbei sind P und L Integergrößen und Z ein Character. Übertragen werden die Binärdarstellungen von P, L und Z.

• Nach der Übertragung wird das Sliding Window um eine oder mehrere Positionen nach rechts verschoben und es beginnt der nächste Codierschritt i + 1.

Die obere Grafik zeigt die Anfangsbelegung mit Puffergröße G = 4 zu den Zeitpunkten i = 1 sowie i = 4. Zum Zeitpunkt i = 1 ist der Suchpuffer leer, so dass die Coderausgabe (0, 0, B) lautet. Nach der Verschiebung um eine Position beinhaltet der Suchpuffer ein B, aber keinen String, der mit A anfängt. Das zweite Zahlentriple ist somit (0, 0, A). Die Ausgabe für i = 3 lautet (0, 0, R), da im Suchpuffer auch jetzt keine Zeichenfolge zu finden ist, die mit R beginnt.

Die Momentaufnahme zum Zeitpunkt i = 4 ist ebenfalls in der Grafik angegeben. Gesucht ist nun die Zeichenfolge im Suchpuffer, die mit dem Vorschautext BARA am besten übereinstimmt. Übertragen wird wieder ein Zahlentriple (P, L, Z), aber nun mit folgender Bedeutung:

• P gibt die Position im (roten) Suchpuffer an, bei der die gefundene Übereinstimmung beginnt. Die jeweiligen P–Werte für die einzelnen Speicherplätze können der Grafik entnommen werden.

• L bezeichnet die Anzahl der Zeichen im Suchpuffer, die beginnend bei P mit dem aktuellen String im Vorschaupuffer übereinstimmen.

• Z bezeichnet schließlich das erste Zeichen im Vorschaupuffer, das sich vom gefundenen Übereinstimmungs–String im Suchpuffer unterscheidet.

Je größer der LZ77–Parameter G ist, um so leichter findet man eine möglichst lange Übereinstimmung. In der Teilaufgabe (4) werden Sie feststellen, dass die LZ77–Codierung mit G = 5 ein besseres Ergebnis liefert als diejenige mit G = 4. Aufgrund der nachfolgenden Binärdarstellung von P wird man allerdings G stets als Zweierpotenz wählen, so dass G mit ld P Bit darstellbar ist (G = 8  ⇒  dreistellige Binärzahl P). Das heißt, ein Sliding Window mit G = 5 hat eher einen geringen Praxisbezug.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 2.2.

Fragebogen

1

Wie lautet die LZ77–Ausgabe mit G = 4 bei Schritt i = 4?

	(0, 0, B),
	(2, 1, A),
	(2, 3, A).

2

Welche Aussage gilt für die gleiche Puffergröße G = 4 bei Schritt i = 5?

	Im Suchpuffer steht BARA.
	Im Vorschaupuffer steht –BAR.
	Die Ausgabe lautet (0, 0, A).

3

Nach welchem Schritt i ist die Codierung beendet?

$G = 4:\ Nach\ i$ = $Codierschritten$

4

Nun gelte G = 5. Nach welchem Schritt i ist dann die Codierung beendet?

$G = 5:\ Nach\ i$ = $Codierschritten$

5

Welche Vorteile hat LZ78 gegenüber LZ77 bei sehr großen Dateien?

	Man findet häufiger bereits abgelegte Phrasen im Wörterbuch.
	Pro Codierschritt müssen weniger Bit übertragen werden.

Musterlösung

Musterlösung

1.  Richtig ist der Lösungsvorschlag 3. Im Vorschaupuffer steht zum betrachteten Zeitpunkt i = 4 die Zeichenfolge BARA, und im Suchpuffer in den letzten drei Stellen BAR:

$$P = 2\hspace{0.05cm},\hspace{0.2cm}L = 3\hspace{0.05cm},\hspace{0.2cm}Z = \boldsymbol{\rm A}\hspace{0.05cm}.$$

2.  Richtig sind die beiden ersten Lösungsvorschläge. Der Bindestrich findet sich zum Zeitpunkt i = 5 nicht im Suchpuffer, so dass (0, 0, –) ausgegeben wird.

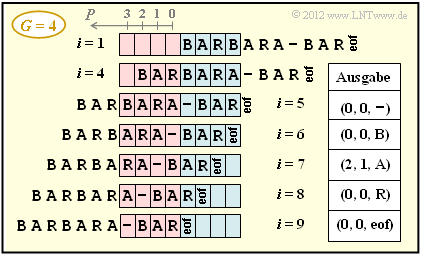
3.  Die folgende Grafik zeigt das Sliding–Window und die Coderausgabe zu den Zeitpunkten i ≥ 5. Nach i = 9 Codierschritten ist der Codiervorgang unter Berücksichtigung von eof beendet.

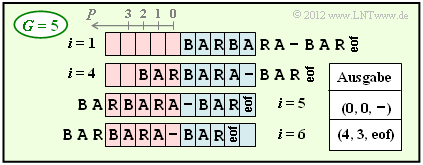
4.  Bei größerer Puffergröße (G = 5 anstelle von G = 4) ist die Codierung schon nach dem Codierschritt i = 6 abgeschlossen. Ein Vergleich der beiden Grafiken zeigt, dass sich für G = 5 gegenüber G = 4 nichts ändert bis einschließlich i = 5. Aufgrund des größeren Puffers lässt sich aber nun BAR gemeinsam mit end–of–file in einem einzigen Schritt codieren, während mit G = 4 hierfür vier Schritte notwendig waren.

5.  Ein Nachteil von LZ77 ist das lokale Wörterbuch. Eigentlich schon bekannte Phrasen können nicht für die Datenkomprimierung verwendet werden, wenn sie mehr als G Zeichen vorher im Text aufgetreten sind. Dagegen sind bei LZ78 alle Phrasen im globalen Wörterbuch abgelegt. Richtig ist Aussage 1.

Die Aussage 2 trifft dagegen nicht zu.

• Richtig ist zwar, dass bei LZ78 nur Pärchen (I, Z) übertragen werden müssen, während bei LZ77 jeder Codierschritt durch ein Triple (P, L, Z) gekennzeichnet ist. Das bedeutet aber noch nicht, dass pro Codierschritt auch weniger Bit übertragen werden müssen.

• Betrachten wir beispielhaft die Puffergröße G = 8. Bei LZ77 muss man dann P mit 3 Bit und L mit 4 Bit dargestellen. Berücksichtigen Sie, dass die gefundene Übereinstimmung zwischen Vorschaupuffer und Suchpuffer auch im Vorschaupuffer enden darf.

• Das neue Zeichen Z benötigt bei LZ78 genau die gleiche Bitanzahl wie bei LZ77 (nämlich 2 Bit), wenn man wie hier vom Symbolumfang M = 4 ausgeht). Die Aussage 2 wäre nur dann richtig, wenn N_I kleiner wäre als N_P + N_L, beispielsweise N_I = 6. Das würde aber bedeuten, dass man die Wörterbuchgröße auf I = 2⁶ = 64 begrenzen müsste. Dies reicht für große Dateien nicht aus.

• Diese Überschlagsrechnung basiert allerdings auf einer einheitlichen Bitanzahl für den Index I. Mit variabler Bitanzahl für den Index kann man etliche Bit einsparen, indem man I nur mit so vielen Bit überträgt, wie es für den Codierschritt i erforderlich ist. Prinzipiell ändert das aber nichts an der Beschränkung der Wörterbuchgröße, was bei großen Dateien stets zu Problemen führen wird.