Aufgaben:Aufgabe 3.11Z: Extrem unsymmetrischer Kanal: Unterschied zwischen den Versionen

Version vom 28. November 2016, 16:29 Uhr

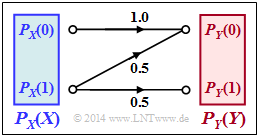
Betrachtet wird der nebenstehend gezeichnete Kanal mit den folgenden Eigenschaften:

Das Symbol $X = 0$ wird immer richtig übertragen und führt stets zum Ergebnis $Y = 0$.
Das Symbol $X = 1$ wird maximal verfälscht. Aus Sicht der Informationstheorie bedeutet diese Aussage:

$${\rm Pr}(Y \hspace{-0.05cm} = 0\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) ={\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = 0.5 \hspace{0.05cm}$$ Zu bestimmen sind in dieser Aufgabe:

die Transinformation $I(X; Y)$für $P_X(0) = p_0 = 0.4$ und $P_X(1) = p_1 = 0.6$. Es gilt allgemein:

$$ I(X;Y) \hspace{-0.15cm} =\hspace{-0.15cm} H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}$$ $$I(X;Y) \hspace{-0.15cm} = \hspace{-0.15cm} H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$$ $$I(X;Y) \hspace{-0.15cm} =\hspace{-0.15cm} H(X) + H(Y)- H(XY)\hspace{0.05cm}$$

die Kanalkapazität:

$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ Hinweis: Die Aufgabe beschreibt einen Teilaspekt von Kapitel 3.3. In der Aufgabe A3.13 sollen die hier gefundenen Ergebnisse im Vergleich zum BSC–Kanal interpretiert werden

Fragebogen

$p_0 = 0.4: H(X)$ =

$bit$

$p_0 = 0.4: H(Y)$ =

$bit$

$p_0 = 0.4: H(XY)$ =

$bit$

$p_0 = 0.4: I(X; Y)$ =

$bit$

$Maximierung: p_0$ =

$bit$

$C$ =

$bit$

$p_0 gemäß (e): H(X|Y)$ =

$bit$

$H(Y|X)$ =

$bit$

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 20: / Zeile 20: @@
 <quiz display=simple>
-{Multiple-Choice Frage
-|type="[]"}
-- Falsch
-+ Richtig
-{Input-Box Frage
+{Berechnen Sie die Quellenentropie allgemein und für $p_0 = 0.4$
 |type="{}"}
-$\alpha$ = { 0.3 }
+$p_0 = 0.4:   H(X)$ = { 0.971 3% } $bit$
+{Berechnen Sie die Sinkenentropie allgemein und für $p_0 = 0.4$.
+|type="{}"}
+$p_0 = 0.4:   H(Y)$ = { 0.881 3% } $bit$
+{Berechnen Sie die Verbundentropie allgemein und für $p_0 = 0.4$.
+|type="{}"}
+$p_0 = 0.4:   H(XY)$ = { 1.571 3% } $bit$
+{Berechnen Sie die Transinformation allgemein und für $p_0 = 0.4$.
+|type="{}"}
+$p_0 = 0.4:   I(X; Y)$ = { 0.281 3% } $bit$
+{Welche Wahrscheinlichkeit $p_0$ führt zur Kanalkapazität $C$?
+|type="{}"}
+$Maximierung:   p_0$ = { 0.6 3% } $bit$
+{Wie groß ist die Kanalkapazität des vorliegenden Kanals?
+|type="{}"}
+$C$ = { 0.322 3% } $bit$
+{Wie groß sind die bedingten Entropien?
+|type="{}"}
+$p_0 gemäß (e):   H(X|Y)$ = { 0.649 3% } $bit$
+$H(Y|X)$ = { 0.4 3% } $bit$
 </quiz>