Aufgaben:Aufgabe 1.1: Multiplexing beim GSM–System: Unterschied zwischen den Versionen

Version vom 11. Dezember 2016, 16:13 Uhr

oma

Der seit 1992 in Europa etablierte Mobilfunkstandard $\text{GSM}$ (Global System for Mobile Communication) nutzt sowohl Frequenz– als auch Zeitmultiplex, um mehreren Teilnehmern die Kommunikation in einer Zelle zu ermöglichen.

Nachfolgend sind einige Charakteristika des Systems in etwas vereinfachter Form angegeben. Eine exaktere Beschreibung finden Sie im Kapitel 3 des letzten LNTwww–Fachbuches „Beispiele von Nachrichtensystemen”.

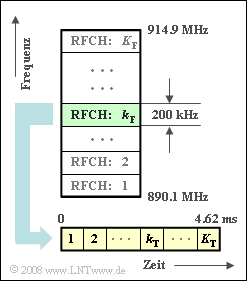
Das Frequenzband des Uplinks (die Verbindung von der Mobil– zur Basisstation) liegt zwischen 890 und 915 MHz. Unter Berücksichtigung der Guard–Bänder (von je 100 kHz) an den beiden Enden steht somit für den Uplink eine Gesamtbandbreite von 24.8 MHz zur Verfügung.
Dieses Band wird von insgesamt $K_F$ Teilkanälen (Radio Frequency Channels) genutzt, die mit einem jeweiligen Abstand von 200 kHz frequenzmäßig nebeneinander liegen. Die Numerierung geschieht mit der Laufvariablen $k_F$, beginnend mit 1.
Der Frequenzbereich für den Downlink (die Verbindung von der Basis– zur Mobilstation) liegt um 45 MHz oberhalb des Uplinks und ist in genau gleicher Weise wie dieser aufgebaut.
Jeder dieser $\text{FDMA}$–Teilkanäle wird gleichzeitig von $K_T$ Teilnehmern per $\text{TDMA}$ (Time Division Multiple Access) genutzt.
Jedem Teilnehmer steht im Abstand von 4.62 Millisekunden ein Zeitschlitz der Dauer T ≈ 577 μs zur Verfügung. Während dieser Zeit müssen die (näherungsweise) 156 Bit übertragen werden, die das Sprachsignal unter Berücksichtigung von Datenreduktion und Kanalcodierung beschreiben.

Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 1.1.

Fragebogen

$K_F$ =

$f_M (k_F = 100)$=

$MHz$

$K_F$=

$K_T$=

$K$=

$R_B$=

$kbit/s$

Musterlösung

1. Aus der Gesamtbandbreite 24.8 $MHz$ und dem Kanalabstand 200 $kHz$ folgt $K_F = 124$.

2. Die Mittenfrequenz des ersten Kanals liegt bei 890.2 MHz. Der mit „RFCH 100” bezeichnete Kanal liegt um $99 · 200 kHz = 19.8 MHz$ höher: $f_M= 890.2 MHz + 19.8 MHz = 910 MHz$

3.Um die Überlegungen zur Teilaufgabe b) nutzen zu können, transformieren wir die Aufgabenstellung in den Uplink. Der gleiche Kanal mit der Kennung $k_F$, der im Downlink die Frequenz 940 $MHz$ nutzt, liegt im Uplink bei 895 $MHz$. Damit gilt $$k_{\rm F} = 1 + \frac {895 \,\,{\rm MHz } - 890.2 \,\,{\rm MHz } }{0.2 \,\,{\rm MHz }} \hspace{0.15cm}\underline {= 25}.$$ 4. In einem $\text{TDMA}$–Rahmen der Dauer 4.62 Millisekunden können $K_T = 8$ Zeitschlitze mit jeweiliger Dauer $T = 577 μs$ untergebracht werden. $K_T = 8$ wird bei $\text{GSM}$ auch tatsächlich verwendet.

5.Mit den Ergebnissen aus (a) und (d) erhält man: $$K = K_{\rm F} \cdot K_{\rm T} = 124 \cdot 8 \hspace{0.15cm}\underline {= 992}$$

6.Während der Zeit $T = 577 μs$ müssen 156 Bit übertragen werden. Damit stehen für jedes Bit die Zeit $T_B = 3.699 μs$ zur Verfügung. Daraus ergibt sich die Bitrate $$R_{\rm B} = \frac {1 }{T_{\rm B}}\hspace{0.15cm}\underline {\approx 270 \,\,{\rm kbit/s }}.$$ Diese Brutto–Bitrate beinhaltet neben den das Sprachsignal beschreibenden Datensymbolen auch die Trainigssequenz zur Kanalschätzung und die Redundanz zur Kanalcodierung. Die Netto–Bitrate beträgt beim $\text{GSM}$–System für jeden der acht Benutzer nur etwa 13 $kbit/s$.

@@ Zeile 47: / Zeile 47: @@
 {{ML-Kopf}}
 '''1.''' Aus der Gesamtbandbreite 24.8 $MHz$ und dem Kanalabstand 200 $kHz$ folgt $K_F = 124$.
 '''2.''' Die Mittenfrequenz des ersten Kanals liegt bei 890.2 MHz. Der mit „RFCH 100” bezeichnete Kanal liegt um $99 · 200 kHz = 19.8 MHz$ höher:
 $f_M= 890.2 MHz + 19.8 MHz = 910 MHz$
 '''3.'''Um die Überlegungen zur Teilaufgabe b) nutzen zu können, transformieren wir die Aufgabenstellung in den Uplink. Der gleiche Kanal mit der Kennung $k_F$, der im Downlink die Frequenz 940 $MHz$ nutzt, liegt im Uplink bei 895 $MHz$. Damit gilt
-$$k_{\rm F} = 1 + \frac {895 \,\,{\rm MHz } - 890.2 \,\,{\rm MHz } }{0.2 \,\,{\rm MHz }} \hspace{0.15cm}\underline {= 25}$$.
+$$k_{\rm F} = 1 + \frac {895 \,\,{\rm MHz } - 890.2 \,\,{\rm MHz } }{0.2 \,\,{\rm MHz }} \hspace{0.15cm}\underline {= 25}.$$
 '''4.'''  In einem $\text{TDMA}$–Rahmen der Dauer 4.62 Millisekunden können $K_T = 8$ Zeitschlitze mit jeweiliger Dauer $T = 577 μs$ untergebracht werden. $K_T = 8$ wird bei $\text{GSM}$ auch tatsächlich verwendet.
 '''5.'''Mit den Ergebnissen aus (a) und (d) erhält man:
-$$K = K_{\rm F} \cdot K_{\rm T} = 124 \cdot 8 \hspace{0.15cm}\underline {= 992}$$.
+$$K = K_{\rm F} \cdot K_{\rm T} = 124 \cdot 8 \hspace{0.15cm}\underline {= 992}$$
 '''6.'''Während der Zeit $T = 577 μs$ müssen 156 Bit übertragen werden. Damit stehen für jedes Bit die Zeit $T_B = 3.699 μs$ zur Verfügung. Daraus ergibt sich die Bitrate
-$$R_{\rm B} = \frac {1 }{T_{\rm B}}\hspace{0.15cm}\underline {\approx 270 \,\,{\rm kbit/s }}$$.
+$$R_{\rm B} = \frac {1 }{T_{\rm B}}\hspace{0.15cm}\underline {\approx 270 \,\,{\rm kbit/s }}.$$
 Diese Brutto–Bitrate beinhaltet neben den das Sprachsignal beschreibenden Datensymbolen auch die Trainigssequenz zur Kanalschätzung und die Redundanz zur Kanalcodierung. Die Netto–Bitrate beträgt beim $\text{GSM}$–System für jeden der acht Benutzer nur etwa 13 $kbit/s$.
-'''7.'''
 {{ML-Fuß}}