Aufgaben:Aufgabe 1.2Z: Linear verzerrendes System: Unterschied zwischen den Versionen

Version vom 11. Dezember 2016, 18:19 Uhr

Modulator, Kanal und Demodulator einer Einrichtung zur Nachrichtenübertragung können durch ein einziges lineares System mit dem Frequenzgang $$ H(f) = {\rm si }( \pi \cdot f \cdot \Delta t)$$ beschrieben werden. Die dazugehörige Impulsantwort ist rechteckförmig, symmetrisch um $t = 0$ und weist die Höhe $1/Δt$ sowie die Dauer Δt auf: $$ h(t) = \left\{ \begin{array}{c} 1/\Delta t \\ 1/(2\Delta t) \\ 0 \\ \end{array} \right. \begin{array}{*{4}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} t\hspace{0.05cm} \right| < \Delta t/2,} \\ {\left| \hspace{0.005cm}t\hspace{0.05cm} \right| = \Delta t/2,} \\ {\left|\hspace{0.005cm} t \hspace{0.05cm} \right| > \Delta t/2.} \\ \end{array}$$

Es handelt sich um einen Spalttiefpass, der im Kapitel 1.3 des Buches „Lineare zeitinvariante Systeme” eingehend behandelt wurde.

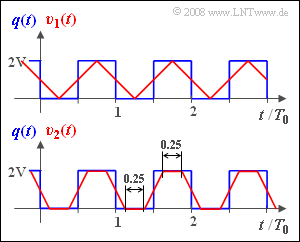
Am Systemeingang liegt das periodische Rechtecksignal $q(t)$ mit der Periodendauer $T_0$ an. Die Dauer der einzelnen Rechtecke und die der Lücken sind jeweils $T_0/2$. Die Höhe der Rechtecke beträgt 2V.

Das Signal $υ(t)$ am Systemausgang wird als Sinkensignal bezeichnet. Dieses ist für zwei verschiedene Parameterwerte der äquivalenten Impulsdauer in der Grafik dargestellt:

Das Signal $υ_1(t)$ ergibt sich, wenn die äquivalente Impulsdauer von $h(t)$ genau $Δt_1$ ist.
Entsprechend ergibt sich das Signal $υ_2(t)$ mit der äquivalenten Impulsdauer $Δt_2$.

Die Veränderung vom Rechtecksignal $q(t)$ zum dreieck- bzw. trapezförmigen Sinkensignal $υ(t)$ ist auf lineare Verzerrungen zurückzuführen und wird durch das Fehlersignal $ε(t) = υ(t) – q(t)$ erfasst. Mit den Leistungen $P_q$ und $P_ε$ der Signale $q(t)$ und $ε(t)$ kann das Sinken–$\text{SNR}$ berechnet werden:

$$\rho_{v} = \frac{P_{q}}{P_{\varepsilon }} \hspace{0.05cm}.$$ Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.2. Die Leistungen $P_q$ und $P_ε$ sind die quadratischen Mittelwerte der Signale $q(t)$ und $ε(t)$ und können bei periodischen Signalen mit der Periodendauer $T_0$ wie folgt ermittelt werden: $$P_{q} = \overline{q(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int\limits_{0}^{ T_{\rm 0}} {q(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}, \hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int\limits_{0}^{ T_{\rm 0}} {\varepsilon(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 10: / Zeile 10: @@
 Es handelt sich um einen Spalttiefpass, der im [http://www.lntwww.de/Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen Kapitel 1.3] des Buches „Lineare zeitinvariante Systeme” eingehend behandelt wurde.
+Am Systemeingang liegt das periodische Rechtecksignal $q(t)$ mit der Periodendauer $T_0$ an. Die Dauer der einzelnen Rechtecke und die der Lücken sind jeweils $T_0/2$. Die Höhe der Rechtecke beträgt 2V.
+Das Signal $υ(t)$ am Systemausgang wird als Sinkensignal bezeichnet. Dieses ist für zwei verschiedene Parameterwerte der äquivalenten Impulsdauer in der Grafik dargestellt:
+:* Das Signal $υ_1(t)$ ergibt sich, wenn die äquivalente Impulsdauer von $h(t)$ genau $Δt_1$ ist.
+:* Entsprechend ergibt sich das Signal $υ_2(t)$ mit der äquivalenten Impulsdauer $Δt_2$.
+Die Veränderung vom Rechtecksignal $q(t)$ zum dreieck- bzw. trapezförmigen Sinkensignal $υ(t)$ ist auf lineare Verzerrungen zurückzuführen und wird durch das Fehlersignal $ε(t) = υ(t) – q(t)$ erfasst. Mit den Leistungen $P_q$ und $P_ε$ der Signale $q(t)$ und $ε(t)$ kann das Sinken–$\text{SNR}$ berechnet werden:
+$$\rho_{v} = \frac{P_{q}}{P_{\varepsilon }} \hspace{0.05cm}.$$
+'''Hinweis:''' Die Aufgabe bezieht sich auf den Theorieteil von [http://www.lntwww.de/Modulationsverfahren/Qualit%C3%A4tskriterien Kapitel 1.2]. Die Leistungen $P_q$ und $P_ε$ sind die quadratischen Mittelwerte der Signale $q(t)$ und $ε(t)$ und können bei periodischen Signalen mit der Periodendauer $T_0$ wie folgt ermittelt werden:
+$$P_{q} = \overline{q(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int\limits_{0}^{ T_{\rm 0}} {q(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}, \hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int\limits_{0}^{ T_{\rm 0}} {\varepsilon(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
 ===Fragebogen===

	Falsch
	Richtig