Digitalsignalübertragung/Berücksichtigung von Kanalverzerrungen und Entzerrung: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 109: | Zeile 109: | ||
Aus obiger Grafik und den bisherigen Erläuterungen geht bereits hervor, dass bei verzerrendem Kanal ⇒ <i>H</i><sub>K</sub>(<i>f</i>) ≠ 1 die Grenzfrequenz <i>f</i><sub>G</sub> · <i>T</i> = 0.8 nicht mehr optimal sein wird.<br> | Aus obiger Grafik und den bisherigen Erläuterungen geht bereits hervor, dass bei verzerrendem Kanal ⇒ <i>H</i><sub>K</sub>(<i>f</i>) ≠ 1 die Grenzfrequenz <i>f</i><sub>G</sub> · <i>T</i> = 0.8 nicht mehr optimal sein wird.<br> | ||
| − | + | == Aufgaben == | |
| + | <br> | ||
== Aufgaben == | == Aufgaben == | ||
Version vom 26. Dezember 2016, 17:46 Uhr
Inhaltsverzeichnis
Idealer Kanalentzerrer (1)
Bei einem Übertragungssystem, dessen Kanalfrequenzgang HK(f) starke Verzerrungen hervorruft, gehen wir von folgendem Blockschaltbild (obere Grafik) und äquivalentem Ersatzschaltbild (untere Grafik) aus.
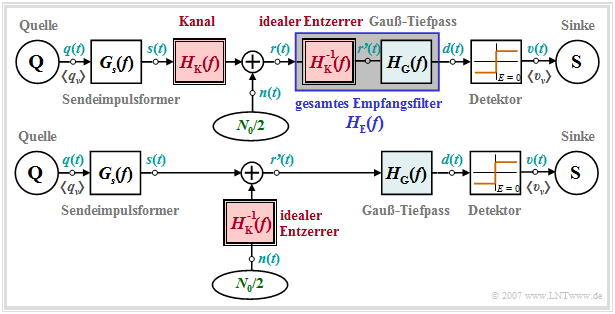
Zu diesen Darstellungen ist Folgendes anzumerken:
- Das Empfangsfilter HE(f) wird – zumindest gedanklich – aus einem idealen Kanalentzerrer 1/HK(f) und einem Tiefpass HG(f) zusammengesetzt. Hierfür verwenden wir in diesem Kapitel beispielhaft einen Gaußtiefpass mit der Grenzfrequenz fG.
- Verschiebt man nun den idealen Entzerrer – wiederum rein gedanklich – auf die linke Seite der Rauschadditionsstelle, so ändert sich bezüglich dem S/N–Verhältnis an der Sinke und bezüglich der Fehlerwahrscheinlichkeit nichts gegenüber dem oben gezeichneten Blockschaltbild.
- Aus dem unteren Ersatzschaltbild erkennt man, dass sich durch den Kanalfrequenzgang HK(f) bezüglich des Detektionsnutzsignals dS(t) nichts ändert, wenn man diesen mit 1/HK(f) vollständig kompensiert. Das Nutzsignal hat somit die genau gleiche Form wie im Kapitel 3.2 berechnet.
- Die Degradation durch den Kanalfrequenzgang HK(f) zeigt sich vielmehr durch eine signifikante Erhöhung der Detektionsstörleistung, also der Varianz des Signals dN(t):
- \[\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} \frac{1}{|H_{\rm K}(f)|^2}\cdot |H_{\rm G}(f)|^2 \,{\rm d} f \hspace{0.05cm}.\]
- Voraussetzung für endliches σd2 ist, dass der Tiefpass HG(f) das Rauschen n(t) bei (sehr) hohen Frequenzen stärker abschwächt, als es vom idealen Entzerrer 1/HK(f) angehoben wird.
Anmerkung: Der Kanalfrequenzgang HK(f) muss nach Betrag und Phase entzerrt werden, allerdings nur in einem von HG(f) vorgegebenen eingeschränkten Frequenzbereich. Eine vollständige Phasenentzerrung ist aber nur auf Kosten einer (frequenzunabhängigen) Laufzeit möglich, die im Folgenden nicht weiter berücksichtigt wird.
Idealer Kanalentzerrer (2)
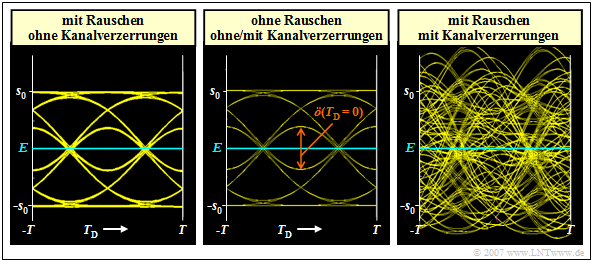
Das linke Augendiagramm ergibt sich bei idealem Kanal, also für HK(f) = 1. Es berücksichtigt das AWGN–Rauschen, das aber hier mit 10 · lg EB/N0 = 30 dB deutlich geringer angenommen wurde als im Kapitel 3.2. Für diese Konfiguration wurde per Simulation ermittelt:
\[10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\approx 26.8\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}< 10^{-40}\hspace{0.05cm}.\]
Dagegen gilt das rechte Diagramm für ein Koaxialkabel, wobei die charakteristische Kabeldämpfung <nobr>a∗ = 40 dB</nobr> beträgt. Hierfür ergeben sich deutlich ungünstigere Systemgrößen:
\[10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\approx -4.6\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}\approx 0.28\hspace{0.05cm}.\]
Dieses Ergebnis kann wie folgt interpretiert werden:
- Unter der Voraussetzung eines idealen Kanalentzerrers ergibt sich das gleiche „Augendiagramm ohne Rauschen” wie beim idealen Kanal HK(f) = 1 (siehe mittlere Grafik).
- Durch die Kanalentzerrung 1/HK(f) wird der Rauschanteil extrem verstärkt. Im rechten Beispiel ist wegen der starken Verzerrung eine weitgehende Entzerrung erforderlich. Die Rauschleistung σd2 ist um den Faktor 1300 größer als links (keine Verzerrung ⇒ keine Entzerrung).
- Eine akzeptable Fehlerwahrscheinlichkeit ergibt sich nur bei kleinerer Rauschleistungsdichte N0. Beispielsweise erhält man mit 10 · lg EB/N0 = 50 dB (statt 30 dB) folgendes Ergebnis:
- \[10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\approx 15.4\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}\approx 2 \cdot 10^{-9}\hspace{0.05cm}.\]
Erhöhung der Rauschleistung durch lineare Entzerrung (1)
Die Augendiagramme auf der letzten Seite dokumentieren eindrucksvoll die Erhöhung der Rauschleistung σd2 bei unveränderter vertikaler Augenöffnung, wenn man den Kanalfrequenzgang HK(f) empfangsseitig durch dessen Inverse kompensiert. Dieses Ergebnis soll nun anhand der Rauschleistungsdichte ΦdN(f) nach dem Empfangsfilter (vor dem Entscheider) interpretiert werden, wobei folgende Einstellungen gelten:
- Der Kanal sei ein Koaxialkabel mit dem Betragsfrequenzgang
- \[|H_{\rm K}(f)| = {\rm exp}\left [- a_{\star}\cdot \sqrt{2 f T}\hspace{0.05cm} \right ]\hspace{0.2cm}{\rm mit}\hspace{0.2cm} a_{\star} = 1.7\,\,{\rm Np}\hspace{0.2cm} ({\rm entsprechend} \hspace{0.2cm} 15\,\,{\rm dB}) \hspace{0.05cm}.\]
- Der ideale Kanalentzerrer HK–1(f) kompensiert den Kanalfrequenzgang vollständig. Über die Realisierung der Dämpfungs– und Phasenentzerrung wird hier keine Aussage getroffen.
- Zur Rauschleistungsbegrenzung wird ein Gaußtiefpass eingesetzt:
- \[|H_{\rm G}(f)| = {\rm exp}\left [- \pi \cdot \left (\frac{f }{2 f_{\rm G}}\right )^2 \right ]\hspace{0.2cm}{\rm mit}\hspace{0.2cm} f_{\rm G} = 0.8/T \hspace{0.2cm} {\rm bzw.} \hspace{0.2cm} f_{\rm G} = 0.4/T \hspace{0.05cm}.\]
Damit gilt für die Rauschleistungsdichte vor dem Entscheider:
\[{\it \Phi}_{d{\rm N}}(f) = \frac{N_0}{2} \cdot \frac{|H_{\rm G }(f)|^2}{|H_{\rm K}(f)|^2} = \frac{N_0}{2} \cdot {\rm exp}\left [2 \cdot a_{\star}\cdot \sqrt{2 f T} - {\pi}/{2} \cdot \left ({f }/{f_{\rm G}}\right )^2 \right ] \hspace{0.05cm}.\]
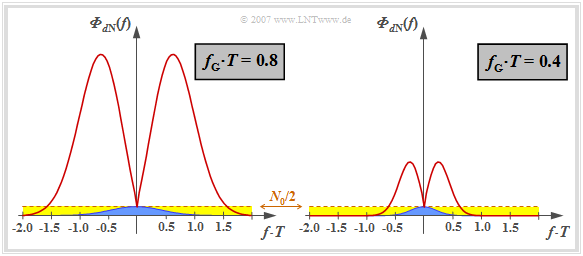
Dieser Verlauf ist nachfolgend für die beiden (normierten) Grenzfrequenzen fG · T = 0.8 (links) bzw. <nobr>fG · T = 0.4</nobr> (rechts) dargestellt. Die Interpretation erfolgt auf der nächsten Seite.
Beachten Sie, dass hier aus Darstellungsgründen die charakteristische Kabeldämpfung mit a∗ = 15 dB (entsprechend 1.7 Np) deutlich kleiner gewählt ist als beim rechten Augendiagramm auf der letzten Seite (gültig für a∗ = 40 dB).
Erhöhung der Rauschleistung durch lineare Entzerrung (2)
Die Grafik zeigt nochmals die Rauschleistungsdichte ΦdN(f) für zwei verschiedene Grenzfrequenzen.
Betrachten wir zunächst die linke Grafik für die (normierte) Grenzfrequenz fG · T = 0.8, die nach den Berechnungen im Kapitel 3.2 für HK(f) = 1 das Optimum darstellt.
- Gelb hinterlegt ist die konstante Rauschleistungsdichte N0/2 am Empfängereingang. Bei idealem Kanal wird diese durch den Gaußtiefpass begrenzt und ergibt die Detektionsrauschleistung σd2 (in der Grafik durch die blaue Fläche gekennzeichnet).
- Werden – wie bei leitungsgebundener Übertragung üblich – höhere Frequenzen stark gedämpft, so steigt |HE(f)|2 aufgrund des idealen Kanalentzerrers sehr stark an, bevor für f · T ≥ 0.6 (nur gültig für a∗ = 15 dB und fG · T = 0.8) der dämpfende Einfluss des Gaußfilters wirksam wird.
- Die Rauschleistung σd2 ist nun gleich der Fläche unter der roten Kurve, die etwa um den Faktor 28 größer ist als die blaue Fläche. Die Auswirkungen dieser unterschiedlichen Rauschleistungen erkennt man auch in den Augendiagrammen auf der letzten Seite, allerdings für a∗ = 40 dB.
Die rechte Grafik zeigt die Rauschleistungsdichte ΦdN(f) für die normierte Grenzfrequenz fG · T = 0.4. Hier wird die Rauschleistung durch den idealen Kanalentzerrer nur noch um den Faktor 9 vergrößert (Verhältnis zwischen der Fläche unter der roten Kurve und der blauen Fläche).
Aus obiger Grafik und den bisherigen Erläuterungen geht bereits hervor, dass bei verzerrendem Kanal ⇒ HK(f) ≠ 1 die Grenzfrequenz fG · T = 0.8 nicht mehr optimal sein wird.
Aufgaben
Aufgaben