Aufgaben:Aufgabe 2.3: ZSB–AM–Realisierung: Unterschied zwischen den Versionen

Version vom 28. Dezember 2016, 16:19 Uhr

Zur Realisierung der so genannten „ZSB–AM mit Träger” soll ein Verstärker mit der Kennlinie $$y = g(x) = U \cdot \left( 1 -{\rm e} ^{-x/U}\right)$$ verwendet werden. Hierbei sind $x = x(t)$ und $y = y(t)$ als zeitabhängige Spannungen am Eingang bzw. Ausgang des Verstärkers zu verstehen. Der Parameter $U = 3 V$ gibt die Sättigungsspannung des Verstärkers an.

Diese Kennlinie wird im Arbeitspunkt $A_0 = 2 V$ betrieben. Dies erreicht man beispielsweise durch das Eingangssignal $$x(t) = A_0 + z(t) + q(t)\hspace{0.05cm}.$$ Setzen Sie für das Trägersignal und das Quellensignal jeweils Cosinusschwingungen voraus: $$ z(t) = A_{\rm T} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} A_{\rm T} = 1\,{\rm V},\hspace{0.2cm} f_{\rm T} = 30\,{\rm kHz},$$ $$ q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} A_{\rm N} = 1\,{\rm V},\hspace{0.2cm} f_{\rm N} = 3\,{\rm kHz}\hspace{0.05cm}.$$ Verwenden Sie bei der Lösung dieser Aufgabe die Hilfsgröße $$w(t) = x(t) - A_0 = z(t) + q(t)\hspace{0.05cm}.$$ Die nichtlineare Kennlinie kann entsprechend einer Taylorreihe um den Arbeitspunkt entwickelt werden: $$y(x) = y(A_0) + \frac{1}{1!} \cdot y\hspace{0.08cm}{\rm '}(A_0) \cdot (x - A_0)+ \frac{1}{2!} \cdot y\hspace{0.08cm}''(A_0) \cdot (x - A_0)^2+$$ $$ + \frac{1}{3!} \cdot y\hspace{0.08cm}'''(A_0) \cdot (x - A_0)^3 + ...$$ In Abhängigkeit der Hilfsgröße $w(t)$ kann das Ausgangssignal dann auch wie folgt dargestellt werden: $$y(t) = c_0 + c_1 \cdot w(t) + c_2 \cdot w^2(t)+ c_3 \cdot w^3(t) + ...$$ Das ZSB–AM–Signal $s(t)$ erhält man durch die Bandbegrenzung von $y(t)$ auf den Frequenzbereich von $\text{23 kHz}$ bis $\text{37 kHz}$. Das heißt: Alle anderen Frequenzen als $f_T$, $f_T±f_N$ sowie $f_T±2f_N$ werden durch den Bandpass entfernt.

Die obige Grafik zeigt die Kennlinie $g(x)$ sowie die Näherungen $g_1(x)$, $g_2(x)$ und $g_3(x)$, wenn man die Taylorreihe nach dem ersten, zweiten oder dritten Term abbricht. Man erkennt, dass die Näherung $g_3(x)$ im dargestellten Bereich innerhalb der Zeichengenauigkeit von $g(x)$ nicht mehr zu unterscheiden ist.

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.1.

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 3: / Zeile 3: @@
 }}
-[[Datei:|right|]]
+[[Datei:P_ID1000__Mod_A_2_3.png|right|]]
+Zur Realisierung der so genannten „ZSB–AM mit Träger” soll ein Verstärker mit der Kennlinie
+$$y = g(x) = U \cdot \left( 1 -{\rm e} ^{-x/U}\right)$$
+verwendet werden. Hierbei sind $x = x(t)$ und $y = y(t)$ als zeitabhängige Spannungen am Eingang bzw. Ausgang des Verstärkers zu verstehen. Der Parameter $U = 3 V$ gibt die Sättigungsspannung des Verstärkers an.
+Diese Kennlinie wird im Arbeitspunkt $A_0 = 2 V$ betrieben. Dies erreicht man beispielsweise durch das Eingangssignal
+$$x(t) = A_0 + z(t) + q(t)\hspace{0.05cm}.$$
+Setzen Sie für das Trägersignal und das Quellensignal jeweils Cosinusschwingungen voraus:
+$$ z(t)  = A_{\rm T} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} A_{\rm T} = 1\,{\rm V},\hspace{0.2cm} f_{\rm T} = 30\,{\rm kHz},$$
+$$ q(t)  =  A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} A_{\rm N} = 1\,{\rm V},\hspace{0.2cm} f_{\rm N} = 3\,{\rm kHz}\hspace{0.05cm}.$$
+Verwenden Sie bei der Lösung dieser Aufgabe die Hilfsgröße
+$$w(t) = x(t) - A_0 = z(t) + q(t)\hspace{0.05cm}.$$
+Die nichtlineare Kennlinie kann entsprechend einer ''Taylorreihe'' um den Arbeitspunkt entwickelt werden:
+$$y(x)  = y(A_0) + \frac{1}{1!} \cdot y\hspace{0.08cm}{\rm '}(A_0) \cdot (x - A_0)+ \frac{1}{2!} \cdot y\hspace{0.08cm}''(A_0) \cdot (x - A_0)^2+$$
+$$ +  \frac{1}{3!} \cdot y\hspace{0.08cm}'''(A_0) \cdot (x - A_0)^3 + ...$$
+In Abhängigkeit der Hilfsgröße $w(t)$ kann das Ausgangssignal dann auch wie folgt dargestellt werden:
+$$y(t) = c_0 + c_1 \cdot w(t) + c_2 \cdot w^2(t)+ c_3 \cdot w^3(t) + ...$$
+Das ZSB–AM–Signal $s(t)$ erhält man durch die Bandbegrenzung von $y(t)$ auf den Frequenzbereich von $\text{23 kHz}$ bis $\text{37 kHz}$. Das heißt: Alle anderen Frequenzen als $f_T$, $f_T±f_N$ sowie $f_T±2f_N$ werden durch den Bandpass entfernt.
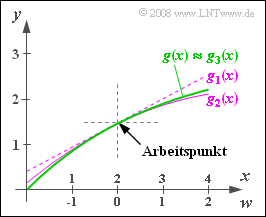
+Die obige Grafik zeigt die Kennlinie $g(x)$ sowie die Näherungen $g_1(x)$, $g_2(x)$ und $g_3(x)$, wenn man die Taylorreihe nach dem ersten, zweiten oder dritten Term abbricht. Man erkennt, dass die Näherung $g_3(x)$ im dargestellten Bereich innerhalb der Zeichengenauigkeit von $g(x)$ nicht mehr zu unterscheiden ist.
+'''Hinweis:''' Diese Aufgabe bezieht sich auf den Theorieteil von [http://www.lntwww.de/Modulationsverfahren/Zweiseitenband-Amplitudenmodulation Kapitel 2.1].

	Falsch
	Richtig