Aufgaben:Aufgabe 2.5: ZSB–AM über einen Gaußkanal: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Synchrondemodulation [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="[…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Modulationsverfahren/Synchrondemodulation | + | {{quiz-Header|Buchseite=Modulationsverfahren/Synchrondemodulation}} |
| − | [[Datei:|right|]] | + | [[Datei:P_ID1010__Mod_A_2_5.png|right|]] |
| + | Das hier betrachtete Übertragungssystem setzt sich aus folgenden Blöcken zusammen: | ||
| + | :*ZSB–AM ohne Träger mit $f_T = 50 kHz$ bzw. $f_T = 55 kHz$: | ||
| + | $$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$ | ||
| + | :* Gaußförmiger Bandpass–Kanalfrequenzgang: | ||
| + | $$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{|f| - f_{\rm M}}{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| + | Der Betrag $|f|$ im Exponenten berücksichtigt, dass $H_K(–f) = H_K(f)$ gilt. | ||
| + | :* Synchrondemodulator mit optimalen Kenngrößen, so dass das Sinkensignal $υ(t)$ vollständig mit dem Quellensignal $q(t)$ übereinstimmt, wenn $H_K(f) = 1$ ist. | ||
| + | Auf der Seite [http://www.lntwww.de/Modulationsverfahren/Synchrondemodulation#Einfluss_linearer_Kanalverzerrungen_.281.29 Einfluss linearer Kanalverzerrungen] wurde gezeigt, dass das gesamte System durch den resultierenden Frequenzgang | ||
| + | $$H_{\rm MKD}(f) = \frac{1}{2} \cdot \left[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\right]$$ | ||
| + | ausreichend genau charakterisiert ist. Der Index steht hierbei für „Modulator–Kanal–Demodulator”. | ||
| + | Das Quellensignal q(t) setzt sich aus zwei Cosinus-Schwingungen zusammen: | ||
| + | $$q(t) = 2\,{\rm V}\cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t)+ 3\,{\rm V}\cdot \cos (2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ | ||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf den Lehrstoff von [http://www.lntwww.de/Modulationsverfahren/Synchrondemodulation Kapitel 2.2]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {Berechnen Sie den resultierenden Frequenzgang $H_{MKD}(f)$ für $f_T = 50 kHz$. Welche Werte ergeben sich für $f = 1 kHz$ und $f = 5 kHz$? | ||
| + | |type="{}"} | ||
| + | $f_T = 50 kHz: |H_{MKD} (f = 1 kHz)|$ = { 0.969 3% } | ||
| + | $f_T = 50 kHz: |H_{MKD} (f = 5 kHz)|$ = { 0.456 3% } | ||
| + | |||
| + | {Berechnen Sie das Sinkensignal $υ(t)$. Geben Sie die Amplituden $A_1$ und $A_5$ des 1 kHz– bzw. 5 kHz–Anteils an. | ||
| + | |type="{}"} | ||
| + | $f_T = 50 kHz: A_1$ = { 1.938 3% } $\text{ V }$ | ||
| + | $f_T = 50 kHz: A_5$ = { 1.368 3% } $\text{ V }$ | ||
| + | |||
| + | |||
| + | {Berechnen Sie den resultierenden Frequenzgang $H_{MKD}(f)$ für $f_T = 55 kHz$. Welche Werte ergeben sich nun für $f = 1 kHz$ und $f = 5 kHz$? | ||
| + | |type="{}"} | ||
| + | $f_T = 55 kHz: |H_{MKD} (f = 1 kHz)|$ = { 0.463 3 % } | ||
| + | $f_T = 55 kHz: |H_{MKD} (f = 5 kHz)|$ = { 0.521 3 % } | ||
| − | { | + | {Berechnen Sie das Sinkensignal $υ(t)$. Geben Sie hierfür die Amplituden $A_1$ und $A_5$ des 1 kHz– bzw. 5 kHz–Anteils an. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $f_T = 55 kHz: A_1$ = { 0.926 3% } $\text{ V }$ |
| + | $f_T = 55 kHz: A_1$ = { 1.563 3% } $\text{ V }$ | ||
| + | {Gibt es eine Trägerfrequenz $f_T$, die bei dem gegebenen Quellensignal und dem gegebenen Kanal zu keinen Verzerrungen führt? Begründen Sie Ihre Antwort. | ||
| + | |type="[]"} | ||
| + | + ja | ||
| + | - nein | ||
Version vom 30. Dezember 2016, 19:01 Uhr
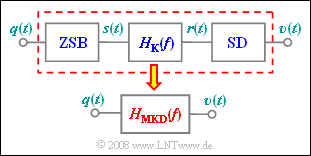
Das hier betrachtete Übertragungssystem setzt sich aus folgenden Blöcken zusammen:
- ZSB–AM ohne Träger mit $f_T = 50 kHz$ bzw. $f_T = 55 kHz$:
$$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$
- Gaußförmiger Bandpass–Kanalfrequenzgang:
$$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{|f| - f_{\rm M}}{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$ Der Betrag $|f|$ im Exponenten berücksichtigt, dass $H_K(–f) = H_K(f)$ gilt.
- Synchrondemodulator mit optimalen Kenngrößen, so dass das Sinkensignal $υ(t)$ vollständig mit dem Quellensignal $q(t)$ übereinstimmt, wenn $H_K(f) = 1$ ist.
Auf der Seite Einfluss linearer Kanalverzerrungen wurde gezeigt, dass das gesamte System durch den resultierenden Frequenzgang $$H_{\rm MKD}(f) = \frac{1}{2} \cdot \left[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\right]$$ ausreichend genau charakterisiert ist. Der Index steht hierbei für „Modulator–Kanal–Demodulator”.
Das Quellensignal q(t) setzt sich aus zwei Cosinus-Schwingungen zusammen: $$q(t) = 2\,{\rm V}\cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t)+ 3\,{\rm V}\cdot \cos (2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 2.2.
Fragebogen
Musterlösung