Digitalsignalübertragung/Beschreibungsgrößen digitaler Kanalmodelle

1. Digitalsignalübertragung
2. Digitale Kanalmodelle
3. Beschreibungsgrößen digitaler Kanalmodelle

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Anwendung analoger Kanalmodelle

Für Untersuchungen von Nachrichtenübertragungssystemen sind geeignete Kanalmodelle von großer Wichtigkeit, weil diese

• Voraussetzung für eine Systemsimulation und –optimierung sind, sowie
  
• gleichbleibende und rekonstruierbare Randbedingungen schaffen.
  
  

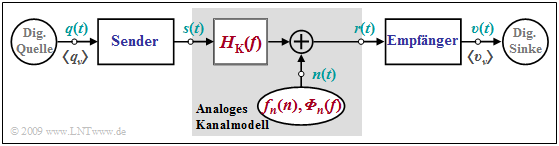
Für die Digitalsignalübertragung gibt es sowohl analoge als auch digitale Kanalmodelle: Ein analoges Kanalmodell muss zwar den Übertragungskanal nicht in allen physikalischen Einzelheiten wiedergeben, sollte jedoch dessen Übertragungsverhalten inklusive der dominanten Störgrößen funktionell ausreichend genau beschreiben. Meist muss ein Kompromiss zwischen mathematischer Handhabbarkeit und dem Bezug zur Realität gefunden werden.

: Die Grafik zeigt ein analoges Kanalmodell innerhalb eines digitalen Übertragungssystems. Dieses beinhaltet den Kanalfrequenzgang H_K(f) zur Beschreibung der linearen Verzerrungen sowie ein additives Störsignal n(t), charakterisiert durch die Wahrscheinlichkeitsdichtefunktion f_n(n) und das Leistungsdichtespektrum Φ_n(f).

Ein Sonderfall dieses Modells ist der so genannte AWGN–Kanal (Additive White Gaussian Noise) mit den Systemeigenschaften

\[H_{\rm K}(f) = 1\hspace{0.05cm},\hspace{0.2cm}{\it \Phi}_{n}(f) = {\rm const.}\hspace{0.05cm},\hspace{0.2cm} {f}_{n}(n) = \frac{1}{\sqrt{2 \pi} \cdot \sigma} \cdot {\rm e}^{-n^2\hspace{-0.05cm}/(2 \sigma^2)}\hspace{0.05cm}.\]

Dieses einfache Modell eignet sich zum Beispiel zur Beschreibung eines Funkkanals mit zeitinvariantem Verhalten, wobei das Kanalmodell dahingehend abstrahiert ist, dass

• der eigentlich bandpassartige Kanal im äquivalenten Tiefpassbereich beschrieben wird, und
  

• die vom Frequenzband und der Übertragungsweglänge abhängige Dämpfung mit der Varianz σ² des Rauschsignals n(t) verrechnet wird.
  
  

Zur Berücksichtigung zeitvarianter Eigenschaften muss man andere Modelle wie Rayleigh–, Rice– und Lognormal–Fading verwenden, die im Buch „Mobile Kommunikation” beschrieben werden.

Bei leitungsgebundenen Übertragungssystemen ist insbesondere der spezifische Frequenzgang des Übertragungsmediums entsprechend den Angaben in Kapitel 4.2 (Koaxialkabel) und Kapitel 4.3 (Zweidrahtleitung) des Buches „Lineare zeitinvariante Systeme” zu berücksichtigen, aber auch, dass aufgrund von Fremdstörungen (Nebensprechen, elektromagnetische Felder, usw.) nicht mehr von Weißem Rauschen ausgegangen werden kann.

Bei optischen Systemen muss zudem das multiplikativ wirkende, also signalabhängige Schrotrauschen geeignet in das analoge Kanalmodell eingearbeitet werden.

Definition digitaler Kanalmodelle (1)

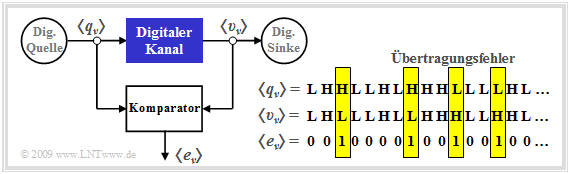
Ein analoges Kanalmodell zeichnet sich durch analoge Eingangs– und Ausgangsgrößen aus. Dagegen sind bei einem digitalen Kanalmodell (manchmal auch als „diskret” bezeichnet) sowohl der Eingang als auch der Ausgang zeit– und wertdiskret. Im Folgenden seien dies die Quellensymbolfolge 〈q_ν〉 ∈ {L, H} und die Sinkensymbolfolge 〈υ_ν〉 ∈ {L, H}. Die Laufvariable ν kann Werte zwischen 1 und N annehmen.

Wie ein Vergleich mit dem Blockschaltbild auf der letzten Seite zeigt, ist der Digitale Kanal ein vereinfachendes Modell des analogen Übertragungskanals einschließlich der technischen Sende– und Empfangseinrichtungen. Vereinfachend deshalb, weil dieses Modell sich lediglich auf die auftretenden Übertragungsfehler bezieht, dargestellt durch die Fehlerfolge 〈e_ν〉 mit

\[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]

Während L und H die möglichen Symbole bezeichnen, die hier für Low und High stehen, ist e_ν ∈ {0, 1} ein reeller Zahlenwert. Oft werden die Symbole auch als q_ν ∈ {0, 1} und υ_ν ∈ {0, 1}definiert. Um Verwechslungen zu vermeiden, haben wir hier die etwas ungewöhnliche Nomenklatur verwendet.

Die in der Grafik angegebene Fehlerfolge 〈e_ν〉

• ergibt sich durch den Vergleich der beiden Binärfolgen 〈q_ν〉 und 〈υ_ν〉,
  
• beinhaltet nur Informationen über die Abfolge der Übertragungsfehler und damit im Allgemeinen weniger Information als ein analoges Kanalmodell,
  
• wird zweckmäßigerweise durch einen Zufallsprozess mit nur wenigen Parametern angenähert.
  
  

Die Fehlerfolge 〈e_ν〉 erlaubt Aussagen über die Fehlerstatistik, zum Beispiel ob es sich um so genannte

• statistisch unabhängige Fehler, oder
  

• Bündelfehler
  
  

handelt. Das folgende Beispiel soll diese beiden Fehlerarten verdeutlichen.