Aufgaben:Aufgabe 2.10: ESB-AM mit Kanalverzerrungen

• Zurück zum Buch

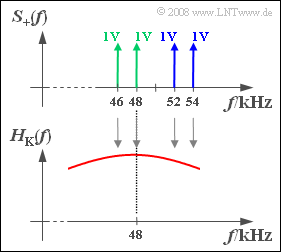
Wir betrachten die Übertragung des Quellensignals $$q(t) = 2\,{\rm V} \cdot \cos(2 \pi f_2 t) + 2\,{\rm V} \cdot \cos(2 \pi f_4 t)$$ über einen Gauß–Bandpasskanal mit der Mittenfrequenz $f_M = 48 kHz$. Diese unterscheidet sich von der bei der Modulation verwendeten Trägerfrequenz $f_T = 50 kHz$. Die Frequenzen $f_2$ und $f_4$ stehen als Abkürzungen für 2 kHz bzw. 4 kHz.

Untersucht werden sollen folgende Modulationsverfahren mit dem jeweiligen Spektrum $S_+(f)$ – des analytischen Signals – entsprechend der oberen Grafik:

• ZSB–AM (alle vier Spektrallinien bei 46 kHz, 48 kHz, 52 kHz und 54 kHz),
• OSB–AM (blaue Spektrallinien bei 52 kHz und 54 kHz),
• USB–AM (grüne Spektrallinien bei 46 kHz und 48 kHz).

Verwendet wird jeweils ein Synchrondemodulator, der zunächst das empfängerseitige Trägersignal $$ z_{\rm E} (t) = \left\{ \begin{array}{c} 2 \cdot z(t) \\ 4 \cdot z(t) \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm ZSB} \hspace{0.05cm}, \\ {\rm OSB, USB} \hspace{0.05cm} \\ \end{array}$$ multiplikativ zusetzt und anschließend die Anteile um die doppelte Trägerfrequenz vollständig unterdrückt. Bei idealem Kanal $H_K(f) = 1$ würde somit in allen Fällen $υ(t) = q(t)$ gelten.

Der hier betrachtete Gaußkanal ist durch folgende Stützwerte gegeben: $$ H_{\rm K}(f = 46\,{\rm kHz}) = 0.968,\hspace{0.3cm}H_{\rm K}(f = 48\,{\rm kHz}) = 1.000,$$ $$ H_{\rm K}(f = 52\,{\rm kHz}) = 0.882,\hspace{0.3cm}H_{\rm K}(f = 54\,{\rm kHz}) = 0.754\hspace{0.05cm}.$$ Schreiben Sie das Sinkensignal jeweils in der Form $$v(t) = A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2)) + A_4 \cdot \cos(2 \pi f_4 \cdot (t - \tau_4))\hspace{0.05cm}.$$ Alle Berechnungen sind sowohl für eine perfekte Phasensynchronisation ($Δϕ_T = 0$) als auch für einen Phasenversatz von $Δϕ_T = 30°$ durchzuführen. Dieser liegt zum Beispiel dann vor, wenn das sendeseitige Trägersignal cosinusförmig verläuft und für das empfangsseitige Trägersignal gilt: $$ z_{\rm E} (t) = A_{\rm E} \cdot \cos(\omega_{\rm T} \cdot t - 30^\circ) . $$ Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.2 und Kapitel 2.4.

Fragebogen

1

Berechnen Sie die Amplituden bei ZSB–AM und perfekter Synchronisation.

$ZSB, Δϕ_T = 0: A_2$ = $V$

$ZSB, Δϕ_T = 0: A_4$ = $V$

2

Wie lauten die Größen A2 und τ2 bei ZSB–AM und $Δϕ_T = 30°$ Phasenversatz?

$ZSB, Δϕ_T = 30°: A_2$ = $V$

$ZSB, Δϕ_T = 30°: τ_2$ = $μs$

3

Berechnen Sie die Amplituden $A_2$ und $A_4$ bei OSB–AM und $Δϕ_T = 0$.

$OSB, Δϕ_T = 0: A_2$ = $V$

$OSB, Δϕ_T = 0: A_4$ = $V$

4

Geben Sie die Signalsamplituden für USB–AM und $Δϕ_T = 0$ an.

$USB, Δϕ_T = 0: A_2$ = $V$

$USB, Δϕ_T = 0: A_4$ = $V$

5

Wie lauten dagegen die Signalparameter bei USB–AM und ΔϕT = 30°?

$USB, Δϕ_T = 30°: A_2$ = $V$

$USB, Δϕ_T = 30°: τ_2$ = $μs$

$USB, Δϕ_T = 30°: A_4$ = $V$

$USB, Δϕ_T = 30°: τ_4$ = $μs$

6

Welche dieser Aussagen sind nach Ihren Ergebnissen zutreffend? Hierbei sollen unter „Kanalverzerrungen” stets Dämpfungsverzerrungen verstanden werden.

	Kanalverzerrung führt bei ZSB-AM zu Dämpfungsverzerrungen.
	Kanalverzerrung führt bei ESB–AM zu Phasenverzerrungen.
	Ein Phasenversatz führt bei ZSB–AM zu Dämpfungsverzerrungen.
	Ein Phasenversatz führt bei ESB–AM zu Phasenverzerrungen.

Musterlösung

Musterlösung

1.Bei der ZSB–AM sind folgende Dämpfungsfaktoren zu berücksichtigen: $$\alpha_2 = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 48\,{\rm kHz}) + H_{\rm K}(f = 52\,{\rm kHz})\right] = 0.981,$$ $$\alpha_4 = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 46\,{\rm kHz}) + H_{\rm K}(f = 54\,{\rm kHz})\right] = 0.861\hspace{0.05cm}.$$ Damit ergeben sich die Amplituden $A_2 = 1.882 V$ und $A_4 = 1.722 V$.

2.Bei ZSB führt ein Phasenversatz zwischen den Trägerfrequenzen von Sender und Empfänger nur zu einer für alle Frequenzen gleichen Dämpfung: $$A_2 = \cos (30^\circ) \cdot 1.882\,{\rm V} \hspace{0.15cm}\underline {= 1.630\,{\rm V}},$$ $$A_4 = \cos (30^\circ) \cdot 1.722\,{\rm V} = 1.491\,{\rm V}\hspace{0.05cm}.$$ Die Laufzeiten $τ_2$ und $τ_4$ sind jeweils 0.

3. Bei OSB–AM wird der Dämpfungsfaktor $α_2$ allein von $H_K(f = 52 kHz)$ bestimmt. Da der prinzipielle Amplitudenverlust der OSB um den Faktor 2 durch eine größere Trägeramplitude ausgeglichen wird, gilt: $$A_2 = 0.882 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.764\,{\rm V}},$$ $$A_4 = 0.754 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.508\,{\rm V}} \hspace{0.05cm}.$$

4. Analog zur Lösung der Teilaufgabe c) erhält man hier: $$ A_2 = H_{\rm K}(f = 48\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 2\,{\rm V}},$$ $$A_4 = H_{\rm K}(f = 46\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.936\,{\rm V}} \hspace{0.05cm}.$$

5.Bei der USB–AM lautet das Empfangssignal: $$r(t) = 1\,{\rm V} \cdot \cos( \omega_{\rm 48} \cdot t) + 0.968\,{\rm V} \cdot \cos( \omega_{\rm 46} \cdot t)\hspace{0.05cm}.$$ Durch Multiplikation mit dem empfangsseitigen Trägersignal $$z_{\rm E}(t) = 4 \cdot \cos( \omega_{\rm 50} \cdot t - \Delta \phi_{\rm T})$$ erhält man nach Anwendung des trigonometrischen Additionstheorems: $$v(t) = r(t) \cdot z_{\rm E}(t) = \hspace{0.15cm}\underline { 2.000\,{\rm V}} \cdot \cos( \omega_{\rm 2} \cdot t - \Delta \phi_{\rm T})+\hspace{0.15cm}\underline { 1.936\,{\rm V}} \cdot \cos( \omega_{\rm 4} \cdot t - \Delta \phi_{\rm T})$$ $$ + ({\rm Anteile \hspace{0.15cm}um \hspace{0.15cm} die \hspace{0.15cm} doppelte \hspace{0.15cm}Tr\ddot{a}gerfrequenz)}\hspace{0.05cm}.$$ Unter Berücksichtigung des nachfolgenden Tiefpassfilters kann hierfür auch geschrieben werden: $$ v(t) = A_2 \cdot \cos( \omega_{\rm 2} \cdot (t - \tau_2))+ A_4 \cdot \cos( \omega_{\rm 4} \cdot (t - \tau_4))\hspace{0.05cm}.$$ Die Amplituden sind gegenüber Teilaufgabe d) unverändert. Für die Laufzeiten erhält man mit $Δϕ_T = π/6$: $$ \tau_2 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_2} = \frac {\pi /6}{2 \pi \cdot 2\,{\rm kHz}} \hspace{0.15cm}\underline {\approx 41.6\,{\rm \mu s}},$$ $$\tau_4 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_4}= \frac {\tau_2}{2}\hspace{0.15cm}\underline {\approx 20.8\,{\rm \mu s}} \hspace{0.05cm}.$$ 6.Richtig sind der erste und der letzte Lösungsvorschlag: Auch bei ESB führen Dämpfungsverzerrungen auf dem Kanal ausschließlich zu Dämpfungsverzerrungen bezüglich $υ(t)$. Phasenverzerrungen gibt es nur bei einem Demodulator mit Phasenversatz, wenn eine Einseitenbandmodulation Anwendung findet. Bei der ZSB–AM hätte ein solcher Phasenversatz überhaupt keine Verzerrungen zur Folge, sondern lediglich eine frequenzunabhängige Dämpfung.

Zu Phasenverzerrungen bezüglich $υ(t)$ kommt es natürlich auch, wenn solche bereits auf dem Kanal auftreten, und zwar sowohl bei der ZSB– als auch bei der OSB–AM.