Aufgaben:Aufgabe 4.10Z: Signalraumkonstellation der 16–QAM: Unterschied zwischen den Versionen

Version vom 6. Januar 2017, 00:10 Uhr

Wir betrachten weiter das 16–QAM–Verfahren entsprechend dem im Theorieteil angegebenen Blockschaltbild. Die Grafik zeigt die möglichen komplexen Amplitudenkoeffizienten $a = a_I + j · a_Q$. Für diese Aufgabe soll ebenso wie für die Aufgabe A4.9 vorausgesetzt werden:

Die möglichen Amplitudenkoeffizienten $a_I$ und $a_Q$ der beiden Komponentensignale sind jeweils ±1 und ±1/3.
Der Sendegrundimpuls $g_s(t)$ ist rechteckförmig und weist die Amplitude $g_0 = 1 V$ und die Dauer $T = 1 μs$ auf.
Das Quellensignal $q(t)$ vor dem Seriell–Parallel–Wandler ist binär und redundanzfrei.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.3. Die zu den farbigen Punkten gehörigen Signale sind auf der Angabenseite zur Aufgabe A4.9 in gleicher Farbe dargestellt.

Fragebogen

$R_B$ =

$Mbit/s$

$a = 1 + j: |a|$ =

$arc (a)$ =

$Grad$

$ a = 1/3 + j/3: |a|$ =

$arc (a)$ =

$Grad$

$ a = –1 + j/3: |a|$ =

$arc (a)$ =

$Grad$

$ a = –1 – j/3: |a|$ =

$arc (a)$ =

$Grad$

$N_{|a|}$ =

$N_{arc}$ =

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 5: / Zeile 5: @@
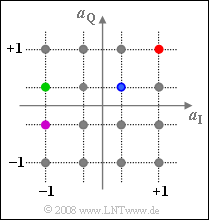
 [[Datei:P_ID1719__Mod_Z_4_9.png|right|]]
 Wir betrachten weiter das 16–QAM–Verfahren entsprechend dem im Theorieteil angegebenen Blockschaltbild. Die Grafik zeigt die möglichen komplexen Amplitudenkoeffizienten $a = a_I + j · a_Q$. Für diese Aufgabe soll ebenso wie für die [http://www.lntwww.de/Aufgaben:4.9_16%E2%80%93QAM%E2%80%93Signal Aufgabe A4.9] vorausgesetzt werden:
+:* Die möglichen Amplitudenkoeffizienten $a_I$ und $a_Q$ der beiden Komponentensignale sind jeweils ±1 und ±1/3.
+:* Der Sendegrundimpuls $g_s(t)$ ist rechteckförmig und weist die Amplitude $g_0 = 1 V$ und die Dauer $T = 1 μs$ auf.
+:*  Das Quellensignal $q(t)$ vor dem Seriell–Parallel–Wandler ist binär und redundanzfrei.
+'''Hinweis:'''  Die Aufgabe gehört zum Themengebiet von [http://www.lntwww.de/Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation Kapitel 4.3]. Die zu den farbigen Punkten gehörigen Signale sind auf der Angabenseite zur Aufgabe A4.9 in gleicher Farbe dargestellt.
 ===Fragebogen===
 <quiz display=simple>
-{Multiple-Choice Frage
+{Wie groß ist die Bitrate des binären Quellensymbols?
-|type="[]"}
+|type="{}"}
-- Falsch
+$R_B$ = { 4 3% } $Mbit/s$
-+ Richtig
-{Input-Box Frage
+{Geben Sie den Betrag und die Phase (zwischen ±180°) für das rote Symbol an.
+|type="{}"}
+$a = 1 + j:   |a|$ = { 1.414n 3% }
+$arc (a)$ = { 45 3% } $Grad$
+{Geben Sie den Betrag und die Phase für das blaue Symbol an.
 |type="{}"}
-$\alpha$ = { 0.3 }
+$ a = 1/3 + j/3:   |a|$ = { 0.471 3% }
+$arc (a)$ = { 45 3% } $Grad$
+{Geben Sie den Betrag und die Phase für das grüne Symbol an.
+|type="{}"}
+$ a = –1 + j/3:   |a|$ = { 1.054 3% }
+$arc (a)$ = { 161.57 3% } $Grad$
+{Geben Sie den Betrag und die Phase für das violette Symbol an.
+|type="{}"}
+$ a = –1 – j/3:   |a|$ = { 1.054 3% }
+$arc (a)$ = { 161.57 3% } $Grad$
+{Wieviele unterschiedliche Beträge ($N_{|a|}$) = und Phasenlagen ($N_{arc}$) sind möglich?
+|type="{}"}
+$N_{|a|}$ = { 3 3% }
+$N_{arc}$ = { 12 3% }
 </quiz>