Aufgaben:Aufgabe 4.15Z: MSK–Grundimpuls und MSK-Spektrum: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modualtionsverfahren/Nichtlineare Modulationsverfahren }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choic…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1744__Mod_Z_4_14.png|right|]] |
| + | Der zur Realisierung der [http://www.lntwww.de/Modulationsverfahren/Nichtlineare_Modulationsverfahren#Realisierung_der_MSK_als_Offset.E2.80.93QPSK_.281.29 MSK mittels Offset–QPSK] stets erforderliche Grundimpuls hat die Form: | ||
| + | $$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} | t | \le T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array$$ | ||
| + | Dieser ist in der Grafik oben dargestellt. Darunter gezeichnet ist die Spektralfunktion $G(f)$, also die Fouriertransformierte von $g(t)$. Die dazugehörige Gleichung soll in dieser Aufgabe ermittelt werden, wobei zu berücksichtigen ist: | ||
| + | $$g(t) = c(t) \cdot r(t)\hspace{0.05cm}.$$ | ||
| + | Hierbei bezeichnet | ||
| + | :* $c(t)$ eine Cosinusschwingung mit Amplitude 1 und (noch zu bestimmender) Frequenz $f_0$, | ||
| + | :* $r(t)$ eine Rechteckfunktion mit der Amplitude $g_0$ und der Dauer 2T. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe gehört zum Themengebiet von [http://www.lntwww.de/Modulationsverfahren/Nichtlineare_Modulationsverfahren Kapitel 4.4]. Das hier gewonnene Ergebnis wird auch in der [http://www.lntwww.de/Aufgaben:4.14_BPSK%E2%80%93QPSK%E2%80%93MSK Aufgabe A4.14] verwendet. | ||
Version vom 6. Januar 2017, 16:55 Uhr
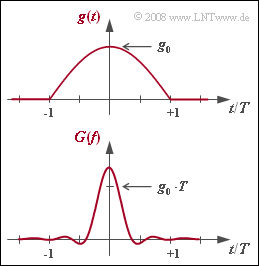
Der zur Realisierung der MSK mittels Offset–QPSK stets erforderliche Grundimpuls hat die Form: $$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} | t | \le T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array$$ Dieser ist in der Grafik oben dargestellt. Darunter gezeichnet ist die Spektralfunktion $G(f)$, also die Fouriertransformierte von $g(t)$. Die dazugehörige Gleichung soll in dieser Aufgabe ermittelt werden, wobei zu berücksichtigen ist: $$g(t) = c(t) \cdot r(t)\hspace{0.05cm}.$$ Hierbei bezeichnet
- $c(t)$ eine Cosinusschwingung mit Amplitude 1 und (noch zu bestimmender) Frequenz $f_0$,
- $r(t)$ eine Rechteckfunktion mit der Amplitude $g_0$ und der Dauer 2T.
Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.4. Das hier gewonnene Ergebnis wird auch in der Aufgabe A4.14 verwendet.
Fragebogen
Musterlösung