Aufgaben:Aufgabe 5.7: OFDM–Sender mittels IDFT: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1662__A_5_7.png|right|]] |
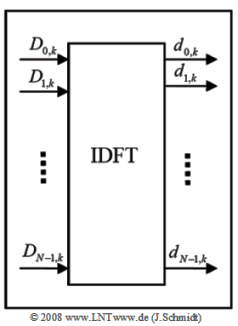
| + | In dieser Aufgabe wird ein OFDM–Sender genauer betrachtet, der mit Hilfe der Inversen Diskreten Fouriertransformation (IDFT) realisiert wird. Dabei gelte: | ||
| + | :* Das System habe N = 4 Träger. | ||
| + | :* Die Rahmendauer sei $T_R = 0.25 ms$. | ||
| + | :* Ein Guard–Intervall wird nicht verwendet. | ||
| + | :* In einem Rahmen werden 16 Bit übertragen. | ||
| + | Die Grafik zeigt den Block IDFT der OFDM–Senderstruktur. Jeweils vier Bit ergeben hierbei ein komplexes Symbol gemäß der unten gegebenen 16–QAM–Signalraumzuordung. | ||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf das [http://www.lntwww.de/Modulationsverfahren/Realisierung_von_OFDM-Systemen Kapitel 5.6] dieses Buches sowie auf [http://www.lntwww.de/Signaldarstellung/Diskrete_Fouriertransformation_(DFT) Kapitel 5.2] des Buches „Signaldarstellung”. Die Gleichung der IDFT lautet mit ν = 0, ... , N–1: | ||
| + | $$d_{\nu ,k} = \sum\limits_{\mu = 0}^{N - 1} {D_{\mu ,k} \cdot w^{ - \nu \cdot \mu } } \quad {\rm{mit}} \quad w = {\rm{e}}^{ - {\rm{j}} {\rm{2\pi}}/N}.$$ | ||
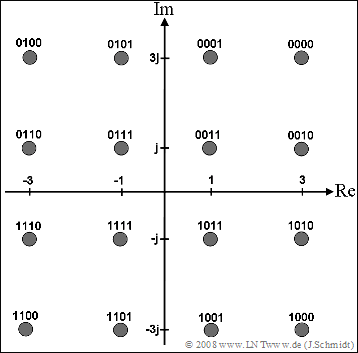
| + | Für die 16–QAM soll in dieser Aufgabe von folgender Signalraumkonstellation ausgegangen werden: | ||
| + | [[Datei:P_ID1666__A_5_7_Signalraum.png]] | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 7. Januar 2017, 20:05 Uhr
In dieser Aufgabe wird ein OFDM–Sender genauer betrachtet, der mit Hilfe der Inversen Diskreten Fouriertransformation (IDFT) realisiert wird. Dabei gelte:
- Das System habe N = 4 Träger.
- Die Rahmendauer sei $T_R = 0.25 ms$.
- Ein Guard–Intervall wird nicht verwendet.
- In einem Rahmen werden 16 Bit übertragen.
Die Grafik zeigt den Block IDFT der OFDM–Senderstruktur. Jeweils vier Bit ergeben hierbei ein komplexes Symbol gemäß der unten gegebenen 16–QAM–Signalraumzuordung.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel 5.6 dieses Buches sowie auf Kapitel 5.2 des Buches „Signaldarstellung”. Die Gleichung der IDFT lautet mit ν = 0, ... , N–1:
$$d_{\nu ,k} = \sum\limits_{\mu = 0}^{N - 1} {D_{\mu ,k} \cdot w^{ - \nu \cdot \mu } } \quad {\rm{mit}} \quad w = {\rm{e}}^{ - {\rm{j}} {\rm{2\pi}}/N}.$$
Für die 16–QAM soll in dieser Aufgabe von folgender Signalraumkonstellation ausgegangen werden:
Fragebogen
Musterlösung