Aufgabe 2.2Z: Nichtlinearitäten

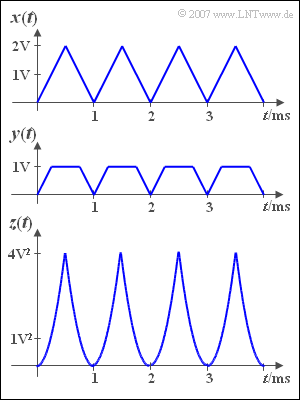
Wir gehen von dem dreieckförmigen Signal ${x(t)}$ gemäß der oberen Abbildung aus. Gibt man dieses Signal auf einen Amplitudenbegrenzer, so entsteht das Signal

$$y(t)=\left\{ {x(t)\atop \rm 1V}{\hspace{0.5cm} {\rm f\ddot{u}r}\quad x(t)\le \rm 1V \atop {\rm sonst}}\right..$$

Eine zweite Nichtlinearität liefert das Signal

$$z(t)=x^2(t).$$

Die Gleichsignalanteile werden nachfolgend mit $x_0$, $y_0$ bzw. $z_0$ bezeichnet.

Hinweise:

Die Aufgabe gehört zum Kapitel Gleichsignal - Grenzfall eines periodischen Signals.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

Musterlösung

1. Der Gleichsignalanteil $x_0$ ist der Mittelwert des Signals $\text{x(t)}$. Es genügt die Mittelung über eine Periodendauer $T_0 = 1 \text{ms}$, und man erhält:

$$x_0=\frac{1}{T_0}\int^{T_0}_0 x(t)\,{\rm d} t \hspace{0.15cm}\underline{=1\rm V}.$$

2. In der Hälfte der Zeit ist $\text{y(t)} = 1 \text{V}$, in der anderen Hälfte liegt es zwischen $0$ und $1 \text{V}$ mit dem Mittelwert bei $0.5 \text{V}$. Daraus folgt $y_0 \underline{= 0.75 \text{V}}$.

3.Aufgrund der Periodizität und der Symmetrie genügt die Mittelung über den Zeitbereich von $0$ bis $T_0/2$. Mit der entsprechenden Kennlinie gilt dann:

$$z_0=\frac{1}{T_0/2}\int^{T_0/2}_0 x^2(t)\,{\rm d}t=\frac{4\rm V^2}{T_0/2}\int^{T_0/2}_0 ({2t}/{T_0})^2\, {\rm d}t={4}/{3}\rm \;V^2 \hspace{0.15cm}\underline{\approx1.333\rm \;V^2}.$$