Aufgabe 4.5: Transinformation aus 2D-WDF

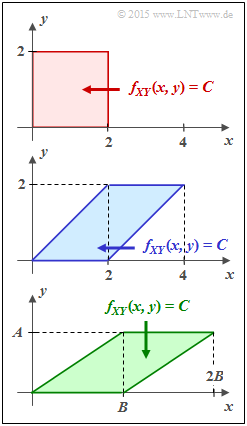
Vorgegeben sind hier die drei unterschiedlichen 2D–Gebiete f_XY(x, y), die in der Aufgabe nach ihren Füllfarben mit

rote Verbund-WDF
blaue Verbund-WDF
grüne Verbund-WDF

bezeichnet werden. In den dargestellten Gebieten gelte jeweils f_XY(x, y) = C = const.

Die Transinformation zwischen den wertkontinuierlichen Zufallsgrößen X und Y kann unter anderem nach folgender Gleichung berechnet werden: $$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$

Für die hier verwendeten differentiellen Entropien gelten die folgenden Gleichungen: $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},$$ $$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y \hspace{0.05cm},$$ $$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} [ f_{XY}(x, y) ] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ Für die beiden Randwahrscheinlichkeitsdichtefunktionen gilt dabei: $$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}y\hspace{0.05cm},\hspace{0.8cm} f_Y(y) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.05cm}.$$ Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.2. Gegeben seien zudem folgende differentielle Entropien:

Ist X dreieckverteilt zwischen x_min und x_max, so gilt:

$$h(X) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}\sqrt[[:Vorlage:\rm e]] \cdot (x_{\rm max} - x_{\rm min})/2\hspace{0.05cm}]\hspace{0.05cm}.$$

Ist Y gleichverteilt zwischen y_min und y_max, so gilt:

$$h(Y) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}]\hspace{0.05cm}.$$

Alle Ergebnisse sollen in „bit” angegeben werden. Dies erreicht man mit „log” ⇒ „log₂”.

Fragebogen

$rote Verbund–WDF: I(X; Y)$ =

$blaue Verbund–WDF: I(X; Y)$ =

$grüne Verbund–WDF: I(X; Y)$ =

	Die Verbund-WDF f_XY(x, y) ergibt ein Parallelogramm.
	Eine der Zufallsgrößen (X oder Y) ist gleichverteilt.
	Die andere Zufallsgröße (Y oder X) ist dreieckverteilt.

Musterlösung

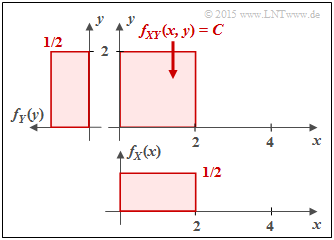
a) Bei der rechteckförmigen Verbund–WDF f_XY(x, y) gibt es zwischen X und Y keine statistischen Bindungen ⇒ I(X; Y) = 0.

Formal lässt sich dieses Ergebnis mit der folgenden Gleichung nachweisen:

$$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$ Die rote Fläche 2D–WDF f_XY(x, y) ist F = 4. Da f_XY(x, y) in diesem Gebiet konstant ist und das Volumen unter f_XY(x, y) gleich 1 sein muss, gilt C = 1/F = 1/4. Daraus folgt für die differentielle Verbundentropie in „bit”: $$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\\ = \ {\rm log}_2 \hspace{0.1cm} (4) \cdot \hspace{0.02cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$ Es ist berücksichtigt, das das Doppelintegral gleich 1 ist. Die Pseudo–Einheit „bit” korrespondiert mit dem Logarithmus dualis ⇒ „log₂”. Weiterhin gilt:

Die beiden Randwahrscheinlichkeitsdichtefunktionen f_X(x) und f_Y(y) sind jeweils rechteckförmig ⇒ Gleichverteilung zwischen 0 und 2:

$$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$

Setzt man diese Ergebnisse in die obige Gleichung ein, so erhält man:

$$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} \hspace{0.05cm}.$$

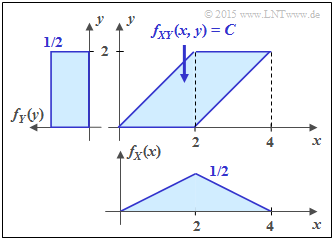
b) Auch bei diesem Parallelogramm ergibt sich F = 4, C = 1/4 sowie h(XY) = 2 bit. Die Zufallsgröße Y ist hier wie in der Teilaufgabe (a) zwischen 0 und 2 gleichverteilt. Somit gilt weiter h(Y) = 1 bit.

Dagegen ist X dreieckverteilt zwischen 0 und 4 (mit Maximum bei 2). Es ergibt sich hierfür die gleiche differentielle Entropie h(Y) wie bei einer symmetrischen Dreieckverteilung im Bereich zwischen ±2 (siehe Angabenblatt): $$h(X) = {\rm log}_2 \hspace{0.1cm} [\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}] = 1.721 \,{\rm bit}$$ $$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} \hspace{0.05cm}.$$

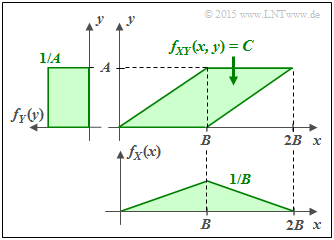
c) Bei den grünen Gegebenheiten berechnet sich die Verbundentropie wie folgt:

3. 4. 5. 6. 7.