Aufgabe 1.3: Entropienäherungen

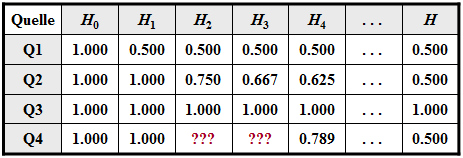
Die Grafik zeigt vier Symbolfolgen $\langle q_\nu \rangle $mit jeweilger Länge $N = 60$. Die Quellensymbole sind jeweils $\rm A$ und $\rm B$. Daraus folgt direkt, dass für den Entscheidungsgehalt aller betrachteten Quellen $H_0 = 1 \; \rm bit/Symbol$ gilt. Die Symbole $\rm A$ und $\rm B$ treten jedoch nicht gleichwahrscheinlich auf, sondern mit den Wahrscheinlichkeiten $p_{\rm A}$ und $p_{\rm B}$.

Die folgende Tabelle zeigt neben $H_0$ noch die Entropienäherungen

$H_1$, basierend auf $p_{\rm A}$ und $p_{\rm B}$ (Spalte 2),
$H_2$, basierend auf Zweiertupel (Spalte 3),
$H_3$, basierend auf Dreiertupel (Spalte 4),
$H_4$, basierend auf Vierertupel (Spalte 5),
die tatsächliche Entropie $H$, die sich aus $H_k$ durch den Grenzübergang für $k \to \infty$ ergibt (letzte Spalte).

Zwischen diesen Entropien bestehen folgende Größenrelationen: $H \le$ ... $\le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$

Nicht bekannt ist die Zuordnung zwischen den Quellen Q1, Q2, Q3, Q4 und den in der Grafik gezeigten gezeigten Symbolfolgen (Schwarz, Blau, Rot, Grün).
Es ist lediglich bekannt, dass die Quelle Q4 einen Wiederholungscode beinhaltet. Aufgrund der Tatsache, dass bei der entsprechenden Symbolfolge jedes zweite Symbol keinerlei Information lierfert, ist $H_0 = 0.5 \; \rm bit/Symbol$. Zudem sind die Entropienäherungen $H_1 = 1 \; \rm bit/Symbol$ (gleichwahrscheinliche Symbole) und $H_4 \approx 0.789 \; \rm bit/Symbol$ gegeben

Zu bestimmen sind für diese Nachrichtenquelle schließlich noch die Entropienäherungen $H_2$ und $H_3$.

Hinweise:

Die Aufgabe gehört zum Kapitel Nachrichtenquellen mit Gedächtnis.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Für die $k$–te Entropienäherung gilt bei Binärquellen ($M = 2$) mit der Verbundwahrscheinlichkeit $ p_i^{(k)}$ eines $k$–Tupels:

$$H_k = \frac{1}{k} \cdot \sum_{i=1}^{2^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_i^{(k)}} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$

Fragebogen

Musterlösung

(1) Die schwarze Binärfolge stammt von der Quelle Q3, da die Symbole gleichwahrscheinlich sind ⇒ $H_1 = H_0$ und keine statistischen Bindungen zwischen den Symbolen bestehen ⇒ $H=$ .... $= H_2 = H_1$.

(2) Man erkennt bei der blauen Binärfolge, dass $\rm A$ sehr viel häufiger auftritt als $\rm B$, so dass $H_1 < H_0$ gelten muss. Entsprechend der Tabelle erfüllt nur die Quelle Q1 diese Bedingung. Aus $H_1 = 0.5 \; \rm bit/Symbol$ kann man die Symbolwahrscheinlichkeiten $p_{\rm A} = 0.89$ und $p_{\rm B} = 0.11$ ermitteln.

(3) Durch Ausschlussverfahren kommt man für die rote Binärfolge zum Quelle Q2: Die Quelle Q1 gehört nämlich zur blauen Folge, Q3 zur schwarzen und Q4 zum Wiederholungscode und damit offensichtlich zur grünen Symbolfolge. Die rote Symbolfolge weist folgende Eigenschaften auf:

Wegen $H_1 = H_0$ sind die Symbole gleichwahrscheinlich: $p_{\rm A} = p_{\rm B} = 0.5$.
Wegen $H < H_1$ bestehen statistische Bindungen innerhalb der Folge. Diese erkennt man daran, dass es zwischen $\rm A$ und $\rm B$ mehr Übergänge als bei statistischer Unabhängigkeit gibt.

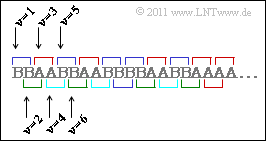
(4) Bei der grünen Symbolfolge (Quelle Q4) sind die Symbole $\rm A$ und $\rm B$ gleichwahrscheinlich:

Symbolfolgen eines binären Wiederholungscodes

$$p_{\rm A} = p_{\rm B} = 0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}H_1 = 1\,{\rm bit/Symbol} \hspace{0.05cm}.$$

Zur $H_2$-Ermittlung betrachtet man Zweiertupel. Die Verbundwahrscheinlichkeiten $p_{\rm AA}$, $p_{\rm AB}$, $p_{\rm PA}$ und $p_{\rm BB}$ können daraus berechnet werden. Aus der Skizze erkennt man:

Die Kombinationen $\rm AB$ und $\rm BA$ sind nur dann möglich, wenn ein Tupel bei geradzahligem $\nu$ beginnt. Für die Verbundwahrscheinlichkeiten $p_{\rm AB}$ und $p_{\rm BA}$ gilt dann:

$$p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}(\nu {\rm \hspace{0.15cm}ist\hspace{0.15cm}gerade}) \cdot {\rm Pr}( q_{\nu} = \mathbf{A}) \cdot {\rm Pr}(q_{\nu+1} = \mathbf{B}\hspace{0.05cm} | q_{\nu} = \mathbf{A}) = {1}/{2} \cdot {1}/{2} \cdot {1}/{2} = {1}/{8} = p_{\rm BA} \hspace{0.05cm}.$$

Dagegen gelten für die beiden weiteren Kombinationen $\rm AA$ und $\rm BB$:

$$p_{\rm AA} ={\rm Pr}(\nu = 1) \cdot {\rm Pr}( q_1 = \mathbf{A}) \cdot {\rm Pr}(q_{2} = \mathbf{A}\hspace{0.05cm} | q_{1} = \mathbf{A}) + {\rm Pr}(\nu=2) \cdot {\rm Pr}( q_{2} = \mathbf{A}) \cdot {\rm Pr}(q_{3} = \mathbf{A}\hspace{0.05cm} | q_{2} = \mathbf{A}) \hspace{0.05cm}.$$

$$\Rightarrow \hspace{0.3cm}p_{\rm AA} = \frac{1}{2} \cdot \frac{1}{2} \cdot 1+ \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{3}{8} = p_{\rm BB} \hspace{0.05cm}.$$

Hierbei steht $\nu = 1$ für alle ungeradzahligen $\nu$ und $\nu = 2$ für alle geradzahligen.

Damit ergibt sich für die Entropienäherung:

$$H_2 = \frac{1}{2} \cdot \left [ 2 \cdot \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}\frac {8}{3} + 2 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8)\right ] = \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) - \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}(3) + \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(5) Nach ähnlichem Vorgehen kommt man bei Dreiertupeln zu den Verbundwahrscheinlichkeiten

$$p_{\rm AAA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm BBB} = 1/4 \hspace{0.05cm},\hspace{0.2cm} p_{\rm ABA} = p_{\rm BAB} = 0 \hspace{0.05cm},$$

$$ p_{\rm AAB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABB} = p_{\rm BBA} = p_{\rm BAA} = 1/8$$

und daraus zur Entropienäherung

$$H_3 = \frac{1}{3} \cdot \left [ 2 \cdot \frac{1}{4} \cdot {\rm log}_2\hspace{0.1cm}(4) + 4 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8)\right ] = \frac{2.5}{3} \hspace{0.15cm} \underline {= 0.833 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

Zur Berechnung von$H_4$ ergeben sich folgende $16$ Wahrscheinlichkeiten:

$$p_{\rm AAAA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm BBBB} = 3/16 \hspace{0.05cm},\hspace{0.2cm} p_{\rm AABB} = p_{\rm BBAA} = 2/16 \hspace{0.05cm},$$

$$ p_{\rm AAAB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABBA} = p_{\rm ABBB} = p_{\rm BBBA} = p_{\rm BAAB} = p_{\rm BAAA}= 1/16 \hspace{0.05cm}$$

$$ p_{\rm AABA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABAA} = p_{\rm ABAB} = p_{\rm BBAB} = p_{\rm BABB} = p_{\rm BABA}= 0\hspace{0.05cm}.$$

Daraus folgt:

$$H_4= \frac{1}{4} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\left [ 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{3}{16} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.1cm}\frac{16}{3} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{1}{8} \hspace{-0.05cm}\cdot \hspace{-0.05cm}{\rm log}_2\hspace{0.1cm}(8) + 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{1}{16} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.1cm}(16)\right ] =\frac{\left [ 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(16) - 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(3) + 4 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(8) + 6\hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(16)\right ]}{32} .$$

Man erkennt: Auch die Näherung $H_4 = 0.789\,{\rm bit/Symbol}$ weicht noch weit vom Entropie-Endwert $H = 0.5\,{\rm bit/Symbol}$ ab.

Hinweis: Der Wiederholungscode kann offensichtlich nicht durch eine Markovquelle modelliert werden. Wäre Q4 eine Markovquelle, so müsste nämlich gelten:

$$H = 2 \cdot H_2 - H_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}H_2 = 1/2 \cdot (H+H_1) = 1/2 \cdot (0.5+1) = 0.75 \,{\rm bit/Symbol}\hspace{0.05cm}.$$

	Q1,
	Q2,
	Q3,
	Q4.

	Q1,
	Q2,
	Q3,
	Q4.

	Q1,
	Q2,
	Q3,
	Q4.