Aufgabe 2.2Z: Mittlere Codewortlänge

Ziel von Datenkomprimierung ist es, die Nachricht einer Quelle mit möglichst wenigen Binärzeichen darzustellen.

Wir betrachten hier eine wertdiskrete Nachrichtenquelle mit dem Symbolvorrat $\{ A, B, C, D\}$ ⇒ Symbolumfang $M = 4$ und den Auftrittswahrscheinlichkeiten

$p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ (Teilaufgabe 1),
$p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ (ab Teilaufgabe 2).

Vorausgesetzt wird, dass es zwischen den einzelnen Quellensymbolen keine statistischen Bindungen gibt.

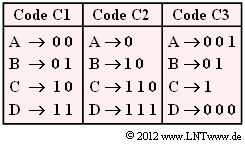
Ein Maß für die Güte eines Komprimierungsverfahrens ist die mittlere Codewortlänge $L_{\rm M}$ mit der Zusatzeinheit „bit/Quellensymbol”. Vorgegeben sind drei Zuordnungen. Anzumerken ist:

Jeder dieser Binärcodes C1, C2 und C3 ist für eine spezielle Quellenstatistik ausgelegt.
Alle Codes sind präfixfrei und somit ohne weitere Angabe sofort decodierbar.

Hinweise:

Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung der Quellencodierung.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

$\text{C1:}\ \ L_{\rm M} \ = $

$\ \rm bit/Quellensymbol$

$\text{C2:}\ \ L_{\rm M} \ = $

$\ \rm bit/Quellensymbol$

$\text{C3:}\ \ L_{\rm M} \ = $

$\ \rm bit/Quellensymbol$

$\text{C1:}\ \ L_{\rm M} \ = $

$\ \rm bit/Quellensymbol$

$\text{C2:}\ \ L_{\rm M} \ = $

$\ \rm bit/Quellensymbol$

$\text{C3:}\ \ L_{\rm M} \ = $

$\ \rm bit/Quellensymbol$

	Kein Codewort ist der Beginn eines anderen Codewortes.
	Alle Codeworte haben gleiche Länge.

	der Code C1,
	der Code C2.

	$\rm AACDBACABADAAA$ ...
	$\rm ACBCCCACAACCD$ ...

Musterlösung

(1) Die mittlere Codewortlänge ergibt sich allgemein zu

$$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}.$$

Sind die vier Quellensymbole gleichwahrscheinlich (alle Wahrscheinlichkeiten genau 1/4), so kann dafür auch geschrieben werden:

$$L_{\rm M} = 1/4 \cdot [ L_{\rm A} + L_{\rm B}+ L_{\rm C} + L_{\rm D}] \hspace{0.05cm}.$$

$\text{Code C1:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.00}\ \rm bit/Quellensymbol$,
$\text{Code C2:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/Quellensymbol$
$\text{Code C3:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/Quellensymbol$.

(2) Mit der Codetabelle C1 ergibt sich unabhängig von den Symbolwahrscheinlichkeiten stets die mittlere Codewortlänge $L_{\rm M} \hspace{0.15cm}\underline{= 2}\ \rm bit/Quellensymbol$. Für die beiden anderen Codes erhält man:

$\text{Code C2:}$ $L_{\rm M} = 1/2 \cdot 1 + 1/4 \cdot 2 + 1/8 \cdot 3 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 1.75}\ \rm bit/Quellensymbol$,
$\text{Code C3:}$ $L_{\rm M} = 1/2 \cdot 3 + 1/4 \cdot 2 + 1/8 \cdot 1 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 2.50}\ \rm bit/Quellensymbol$.

Man erkennt aus dem Beispiel das Prinzip:

Wahrscheinliche Symbole werden durch wenige Binärsymbole dargestellt und unwahrscheinliche durch mehr.
Bei gleichwahrscheinlichen Symbolen wählt man am besten auch die Codewortlängen gleich.

(3) Richtig ist Lösungsvorschlag 1: Der Code C1 mit einheitlicher Länge aller Codeworte ist zwar präfixfrei, aber auch andere Codes können präfixfrei sein, zum Beispiel die Codes C2 und C3.

(4) Bereits aus „00” am Anfang erkennt man, dass der Code C2 hier nicht in Frage kommt, da sonst die Quellensymbolfolge mit „AA” beginnen müsste. Tatsächlich wurde der Code C1 verwendet.

(5) Richtig ist der Lösungsvorschlag 2: Der erste Lösungsvorschlag gibt die Quellensymbolfolge für den Code C2 an, wenn die Codesymbolfolge $\rm 001101111001100100111000$ lauten würde.