Aufgabe 3.11: Viterbi-Empfänger und Trellisdiagramm
Aus LNTwww
Version vom 2. November 2017, 19:55 Uhr von Hussain (Diskussion | Beiträge)
Der sog. Viterbi–Empfänger erlaubt eine aufwandsgünstige Realisierung der Maximum–Likelihood–Entscheidungsregel. Er beinhaltet die im Folgenden aufgeführten Systemkomponenten:
- ein an den Sendegrundimpuls angepasse Matched–Filter mit dem Frequenzgang $H_{\rm HF}(f)$ und dem Ausgangssignal $m(t)$,
- einen Abtaster im Abstand der Symboldauer (Bitdauer) $T$, der das zeitkontinuierliche Signal $m(t)$ in die zeitdiskrete Folge $〈m_{\rm \nu}〉$ wandelt,
- ein Dekorrelationsfilter mit dem Frequenzgang $H_{\rm DF}(f)$ zur Entfernung statistischer Bindungen zwischen den Störanteilen der Folge $〈d_{\rm \nu}〉$,
- den Viterbi–Entscheider, der mit einem trellisbasierten Algorithmus die Sinkensymbolfolge $〈\upsilon_{\rm \nu}〉$ gewinnt.
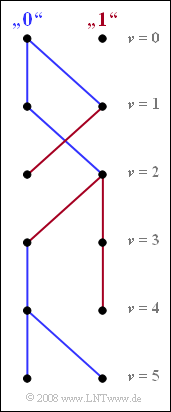
Die Grafik zeigt das vereinfachte Trellisdiagramm der beiden Zustände „$0$” und „$1$” für die Zeitpunkte $\nu ≤ 5$. Dieses Diagramm erhält man als Ergebnis der Auswertung der beiden minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(0)$ und ${\it \Gamma}_{\rm \nu}(1)$ entsprechend der Aufgabe Z3.11.
Gehen Sie in dieser Aufgabe von unipolaren und gleichwahrscheinlichen Amplitudenkoeffizienten aus:
- $${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5 \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Themengebiet Kapitel Viterbi–Empfänger.
- Alle Größen sind hier normiert zu verstehen.
- Die hier angesprochene Thematik wird auch im folgenden Interaktionsmodul behandelt: Eigenschaften des Viterbi–Empfängers.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
(6)