Aufgabe 3.5: GMSK–Modulation

• Zurück zum Buch

GMSK-Modulation

Das bei GSM eingesetzte Modulationsverfahren ist $\color{red} {\rm Gaussian \ Minimum \ Shift Keying}$, kurz GMSK. Es handelt sich hierbei um eine spezielle Art von FSK (Frequency Shift Keying) mit CP–FSK (Phasenanpassung), bei der

• der Modulationsindex den kleinsten Wert besitzt, der die Orthogonalitätsbedingung gerade noch erfüllt: $h = 0.5 \Rightarrow Minimum \ Shift \ Keying$,
• ein Gaußtiefpass mit der Impulsantwort $h_{\rm G}(t)$ vor dem FSK–Modulator, der mit dem Ziel eingebracht ist, so noch weiter Bandbreite einzusparen.

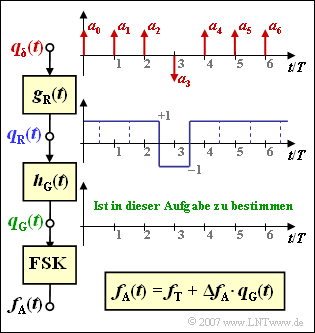
Die Grafik verdeutlicht den Sachverhalt:

Die digitale Nachricht wird durch die Amplitudenkoeffizienten $a_{\mu} ∈ \{±1\}$ repräsentiert, die einem Diracpuls beaufschlagt sind. Anzumerken ist, dass die eingezeichnete Folge für die Teilaufgabe (3) vorausgesetzt wird.

Der Rechteckimpuls sei dimensionslos, symmetrisch und besitze die GSM–Bitdauer $T_{\rm B} = T$:

$$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$

Damit ergibt sich für das Rechtecksignal:

$$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$

Der Gaußtiefpass ist durch seinen Frequenzgang bzw. seine Impulsantwort gegeben:

$$H_{\rm G}(f) = {\rm e}^{-\pi\cdot (\frac{f}{2 f_{\rm G}})^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$

wobei die systemtheoretische Grenzfrequenz $f_{\rm G}$ verwendet wird. In der GSM–Spezifikation wird aber die 3dB–Grenzfrequenz mit $f_{\rm 3dB} = 0.3/T$ angegeben. Daraus kann $f_{\rm G}$ direkt berechnet werden – siehe Teilaufgabe (2).

Das Signal nach dem Gaußtiefpass lautet somit:

$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$

Hierbei wird g(t) als Frequenzimpuls bezeichnet. Für diesen gilt:

$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$

Mit dem tiefpassgefilterten Signal $q_{\rm G}(t)$, der Trägerfrequenz $f_{\rm T}$ und dem Frequenzhub $\Delta f_{\rm A}$ kann somit für die Augenblicksfrequenz am Ausgang des FSK–Modulators geschrieben werden:

$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$

Verwenden Sie für Ihre Berechnungen die beispielhaften Werte $f_{\rm T} = 900 \ \rm MHz$ und $\Delta f_{\rm A} = 68 \ \rm kHz$.

Hinweis:

Die Aufgabe gehört zu Funkschnittstelle im Buch „Beispiele von Nachrichtensystemen” sowie zum Die Charakteristika von GSM dieses Buches. Verwenden Sie zur Lösung der Aufgabe das Gaußintegral:

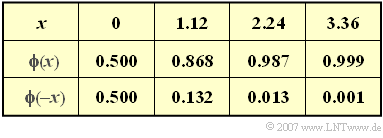
$$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$

$\hspace{15cm}$Insbesondere gilt:

Tabelle der Gaußschen Fehlerfunktion

Fragebogen

1

In welchem Wertebereich kann die Augenblicksfrequenz $f_{\rm A}(t)$ schwanken? Welche Voraussetzungen müssen dafür erfüllt sein?

${\rm Max} \ [f_{\rm A}(t)] \ = \ $ $\ \rm MHz$

${\rm Min} \ [f_{\rm A}(t)] \ = \ $ $\ \rm MHz$

2

Welche systemtheoretische Grenzfrequenz des Gaußtiefpasses ergibt sich aus der Forderung $f_{\rm 3dB} \cdot T = 0.3$?

$f_{\rm G} \cdot T \ = \ $

3

Berechnen Sie den Frequenzimpuls $g(t)$ unter Verwendung der Funktion $\phi (x)$. Wie groß ist der Impulswert $g(t = 0)$?

$g(t = 0) \ = \ $ $\ \rm $

4

Welcher Wert ergibt sich für $q_{\rm G}(t = 3T)$ mit $a_{3} = –1$ sowie $a_{\mu \approx 3} = +1$? Wie groß ist die Augenblicksfrequenz $f_{\rm A}(t = 3T)$?

$q_{\rm G}(t = 3T) \ = \ $

5

Berechnen Sie die Impulswerte $g(t = ±T)$.

$g(t = ±T) \ = \ $

6

Die Amplitudenkoeffizienten seien alternierend. Welcher maximale Betrag von $q_{G}(t)$ ergibt sich bei? Berücksichtigen Sie, dass $g(t ≥ 2 T) \approx 0$ ist.

${\rm Max} \ [|q_{\rm G}(t)|] \ = \ $

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)  (6)  (7)