Aufgabe 2.7: Kohärenzbandbreite
Aus LNTwww
Version vom 20. November 2017, 12:37 Uhr von Hussain (Diskussion | Beiträge)
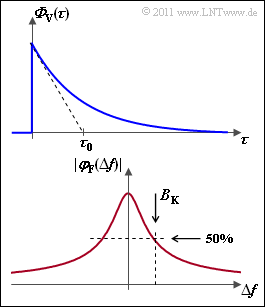
Für das Verzögerungs–Leistungsdichtespektrum wählen wir einen exponentiellen Ansatz. Mit ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$ gilt:
- $$\frac{{\it \Phi}_{\rm V}(\tau)}{{\it \Phi}_{\rm 0}} = {\rm exp}\left ( -\tau / \tau_0 \right ) \hspace{0.05cm}.$$
Die Konstante $\tau_0$ lässt sich entsprechend der oberen Grafik aus der Tangente im Punkt $\tau = 0$ ermitteln. Beachten Sie, dass ${\it \Phi}_{\rm V}(\tau)$ die Einheit $[1/\rm s]$ aufweist. Weiter gilt:
- Die Wahrscheinlichkeitsdichte $f_{\rm V}(\tau)$ hat gleiche Form wie ${\it \Phi}_{\rm V}(\tau)$, ist jedoch auf die Fläche 1 normiert.
- Die mittlere Verzögerungszeit (engl. Average Excess Delay) $m_{\rm V}$ ist gleich dem linearen Erwartungswert $E[\tau]$ und lässt sich aus der WDF $f_{\rm V}(\tau)$ bestimmen.
- Die Mehrwegeverbreiterung (engl. Multipath Spread) $\sigma_{\rm V}$ gibt die Standardabweichung (Streuung) der Zufallsgröße $\tau$ an. Im Theorieteil verwenden wir hierfür auch die Bezeichnung $T_{\rm V}$.
- Die dargestellte Frequenzkorrelationsfunktion $\varphi_{\rm F}(\Delta f)$ kann als die Fouriertransformierte des Verzögerungs–Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$ berechnet werden:
- $$\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$
- Die Kohärenzbandbreite $B_{\rm K}$ ist der $\Delta f$–Wert, bei dem die Frequenzkorrelationsfunktion $\varphi_{\rm F}(\Delta f)$ auf den halben Betrag abgefallen ist.
Hinweise:
- Die Aufgabe gehört zum Themengebiet des Kapitels Das GWSSUS–Kanalmodell
- Benötigt werden Kenntnisse zur Momentenberechnung von Zufallsgrößen aus dem Buch „Stochastische Signaltheorie”.
- Außerdem kann folgende Fouriertransformation als gegeben vorausgesetzt werden:
- $$x(t) = \left\{ \begin{array}{c} {\rm exp}(- \lambda \hspace{0.05cm}\cdot \hspace{0.05cm} t)\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.35cm} {\rm f\ddot{u}r} \hspace{0.15cm} t \ge 0 \\ \hspace{-0.35cm} {\rm f\ddot{u}r} \hspace{0.15cm} t < 0 \\ \end{array} \hspace{0.4cm} {\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.4cm} X(f) = \frac{1}{\lambda + {\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)