Algebraische und polynomische Beschreibung

1. Kanalcodierung
2. Faltungscodierung und geeignete Decoder
3. Algebraische und polynomische Beschreibung

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Definition und Interpretation der Teilmatrizen G0, ... , Gm

Entsprechend den Ausführungen in Kapitel 1.4 lässt sich das Codewort $\underline{x}$ eines linearen Blockcodes aus dem Informationswort $\underline{u}$ und der Generatormatrix $\mathbf{G}$ in einfacher Weise ermitteln:

\[\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.\]

Dabei gilt:

• Die Vektoren $\underline{u}$ und $\underline{x}$ haben die Länge $k$ (Bitanzahl eines Informationswortes) bzw. $n$ (Bitanzahl eines Codewortes) und $\mathbf{G}$ besitzt die Dimension $k × n$ ($k$ Zeilen und $n$ Spalten).
  

• Bei Faltungscodierung bezeichnen dagegen $\underline{u}$ und $\underline{x}$ Sequenzen mit $k' → ∞$ und $n' → ∞$. Deshalb wird auch die Generatormatrix $\mathbf{G}$ in beiden Richtungen unendlich weit ausgedehnt sein.
  
  

Als Vorbereitung für die Einführung der Generatormatrix $\mathbf{G}$ auf der nächsten Seite definieren wir $m + 1$ Teilmatrizen, jeweils mit $k$ Zeilen und $n$ Spalten, die wir mit $\mathbf{G}_l$ bezeichnen, wobei $0 ≤ l ≤ m$ gilt.

: Ist das Matrizenelement $\mathbf{G}_l(\kappa, j) = 1$, so sagt dies aus, dass das Codebit $x_i^{(j)}$ durch das Informationsbit $u_{i–l}^{(\kappa)}$ beeinflusst wird. Andernfalls ist dieses Matrixelement gleich $0$.

Diese Definition wird nun an einem Beispiel verdeutlicht.

:

Wir betrachten wiederum den Faltungscodierer gemäß nebenstehender Grafik mit den folgenden Codebits:

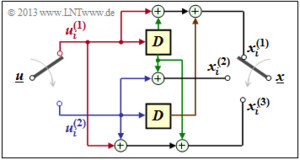
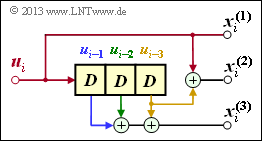
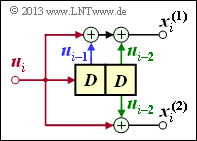
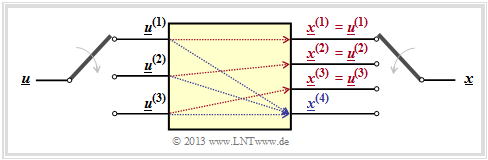
\[x_i^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},\] \[x_i^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},\] \[x_i^{(3)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.\]

Wegen der Gedächtnisordnung $m = 1$ wird dieser Codierer durch die beiden Teilmatrizen $\mathbf{G}_0$ und $\mathbf{G}_1$ charakterisiert:

\[{ \boldsymbol{\rm G}}_0 = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} { \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 & 1 & 1\\ 1 & 0 & 0 \end{pmatrix}\hspace{0.05cm}.\]

Diese Matrizen sind wie folgt zu interpretieren:

• Erste Zeile von $\mathbf{G}_0$, rote Pfeile:       $u_i^{(1)}$ beeinflusst sowohl $x_i^{(1)}$ als auch $x_i^{(3)}$, nicht jedoch $x_i^{(2)}$.
  

• Zweite Zeile von $\mathbf{G}_0$, blaue Pfeile:   $u_i^{(2)}$ beeinflusst $x_i^{(2)}$ und $x_i^{(3)}$, aber nicht $x_i^{(1)}$.
  

• Erste Zeile von $\mathbf{G}_1$, grüne Pfeile:     $u_{i–1}^{(1)}$ beeinflusst alle drei Coderausgänge.
  

• Zweite Zeile von $\mathbf{G}_1$, brauner Pfeil: $u_{i–1}^{(2)}$ beeinflusst nur $x_i^{(1)}$.

Generatormatrix eines Faltungscodierers mit Gedächtnis m

Mit den Teilmatrizen $\mathbf{G}_0, \ ... \ , \mathbf{G}_m$ lassen sich die $n$ Codebits zum Zeitpunkt $i$ wie folgt ausdrücken:

\[\underline{x}_i = \sum_{l = 0}^{m} \hspace{0.15cm}\underline{u}_{i-l} \cdot { \boldsymbol{\rm G}}_l = \underline{u}_{i} \cdot { \boldsymbol{\rm G}}_0 + \underline{u}_{i-1} \cdot { \boldsymbol{\rm G}}_1 + ... + \underline{u}_{i-m} \cdot { \boldsymbol{\rm G}}_m \hspace{0.05cm}.\]

Hierbei sind folgende vektorielle Größen zu berücksichtigen:

\[\underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, u_i^{(k)}\right )\hspace{0.05cm},\hspace{0.5cm} \underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, x_i^{(n)}\right )\hspace{0.05cm}.\]

Betrachtet man die bei $i = 1$ beginnenden und sich zeitlich bis ins Unendliche erstreckenden Sequenzen

\[\underline{\it u} = \big( \underline{\it u}_1\hspace{0.05cm}, \underline{\it u}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it u}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\hspace{0.5cm} \underline{\it x} = \big( \underline{\it x}_1\hspace{0.05cm}, \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it x}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\]

so kann dieser Zusammenhang durch die Matrixgleichung $\underline{x} = \underline{u} \cdot \mathbf{G}$ ausgedrückt werden. Hierbei ist für die Generatormatrix $\mathbf{G}$ zu setzen:

\[{ \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \cdots & \cdots & & & \cdots \end{pmatrix}\hspace{0.05cm}.\]

Aus der Gleichung erkennt man sofort das Gedächtnis $m$ des Faltungscodes. Die Parameter $k$ und $n$ sind direkt nicht ablesbar. Sie sind aber durch die Zeilen– und Spaltenzahl der Teilmatrizen $\mathbf{G}_l$ festgelegt.

:

Mit den zwei Matrizen $\mathbf{G}_0$ und $\mathbf{G}_1$ – siehe letztes Beispiel – erhält man die rechts skizzierte Matrix $\mathbf{G}$.

Anzumerken ist:

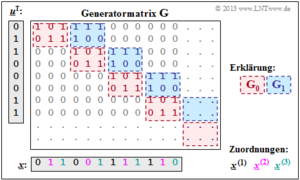
• Die Generatormatrix $\mathbf{G}$ erstreckt sich nach unten und nach rechts eigentlich bis ins Unendliche. Explizit dargestellt sind aber nur 8 Zeilen und 12 Spalten.

• Für die zeitlich begrenzte Informationssequenz $\underline{u} = (0, 1, 1, 0, 0, 0, 1, 1)$ ist der gezeichnete Matrixteil ausreichend. Die Codesequenz lautet dann:   $\underline{x} = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0)$.

• Anhand der Beschriftungsfarben lassen sich die $n = 3$ Codewortstränge ablesen. Das gleiche Ergebnis haben wir (auf anderem Wege) im Beispiel am Ende von Kapitel 3.1 erhalten.

\[\underline{\it x}^{(1)} = (0\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(2)} = (1\hspace{0.05cm}, 0\hspace{0.05cm},1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}.\]

Generatormatrix für Faltungscodierer der Rate 1/n

Wir betrachten nun den Sonderfall $k = 1$, zum einen aus Gründen einer möglichst einfachen Darstellung, aber auch, weil Faltungscodierer der Rate $1/n$ für die Praxis eine große Bedeutung besitzen.

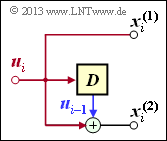
Faltungscodierer mit $k = 1, n = 2$ und $m = 1$

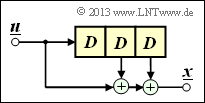
Aus der nebenstehenden Skizze kann abgeleitet werden:

\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 1 \end{pmatrix}\]

\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 01 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 01 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 01 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 01 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]

Für die Eingangssequenz $\underline{u} = (1, 0, 1, 1)$ beginnt die Codesequenz mit $\underline{x} = (1, 1, 0, 1, 1, 1, 1, 0, \ ...)$. Dieses Ergebnis ist gleich der Summe der Zeilen 1, 3 und 4 der Generatormatrix.

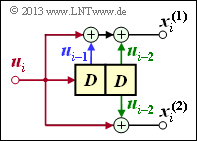
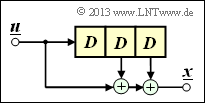
Faltungscodierer mit $k = 1, n = 2$ und $m = 2$

Aufgrund der Gedächtnisordnung $m = 2$ gibt es hier drei Teilmatrizen:

\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_2=\begin{pmatrix} 1 & 1 \end{pmatrix}\]

\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 10 & 11 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 10 & 11 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 10 & 11 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 10 & 11 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]

Hier führt die Eingangsssequenz $\underline{u} = (1, 0, 1, 1)$ zur Codesequenz $\underline{x} = (1, 1, 1, 0, 0, 0, 0, 1, \ ...)$.

Faltungscodierer mit $k = 1, n = 3$ und $m = 3$

Wegen $m = 3$ gibt es vier Teilmatrizen der Dimension $1 × 3$:

\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\]

\[{ \boldsymbol{\rm G}}_2=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_3=\begin{pmatrix} 0 & 1 & 1 \end{pmatrix}\hspace{0.05cm}.\]

Damit lautet die resultierende Generatormatrix:

\[{ \boldsymbol{\rm G}}=\begin{pmatrix} 110 & 001 & 001 & 011 & 000 & 000 & 000 & \cdots & \\ 000 & 110 & 001 & 001 & 011 & 000 & 000 & \cdots & \\ 000 & 000 & 110 & 001 & 001 & 011 & 000 & \cdots & \\ 000 & 000 & 000 & 110 & 001 & 001 & 011 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm},\]

und man erhält für $\underline{u} = (1, 0, 1, 1)$ die Codesequenz $\underline{x} = (1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, \ ...)$.

GF(2)–Beschreibungsformen eines Digitalen Filters (1)

In Kapitel 3.1 wurde bereits darauf hingewiesen, dass ein Faltungscodierer der Rate $1/n$ durch mehrere Digitale Filter realisiert werden kann, wobei die Filter parallel mit der gleichen Eingangsfolge $\underline{u}$ arbeiten. Bevor wir diese Aussage vertiefen, sollen zuerst die Eigenschaften eines Digitalfilters für das Galoisfeld ${\rm GF(2)}$ genannt werden.

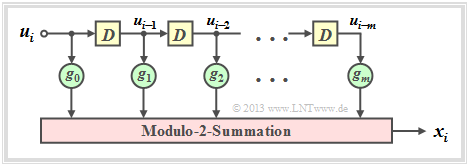
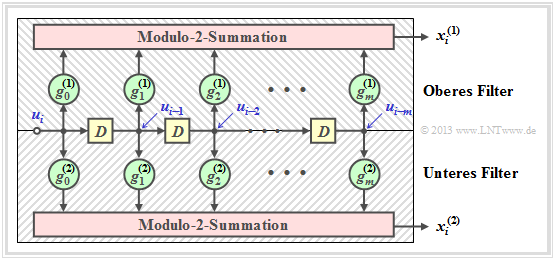
Die Grafik ist wie folgt zu interpretieren:

• Das Filter besitzt die Impulsantwort $\underline{g} = (g_0, g_1, g_2, \ ... \ , g_m)$, wobei für alle Filterkoeffizienten (mit den Indizes $0 ≤ l ≤ m$) gilt:   $g_l ∈ {\rm GF}(2) = \{0, 1\}$.
  

• Die einzelnen Symbole $u_i$ der Eingangsfolge $\underline{u}$ seien ebenfalls binär: $u_i ∈ \{0, 1\}$. Damit gilt für das Ausgangssymbol zu den Zeitpunkten $i ≥ 1$ mit Addition und Multiplikation in ${\rm GF(2)}$:

\[x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l} \hspace{0.05cm}.\]

• Dies entspricht der (zeitdiskreten) Faltungsoperation (englisch: Convolution), gekennzeichnet durch einen Stern. Damit kann für die gesamte Ausgangssequenz geschrieben werden:

\[\underline{x} = \underline{u} * \underline{g}\hspace{0.05cm}.\]

• Wesentlicher Unterschied gegenüber dem Kapitel 5.2 des Buches „Stochastische Signaltheorie” ist die Modulo–2–Addition $(1 + 1 = 0)$ anstelle der herkömmlichen Addition $(1 + 1 = 2)$.
  
  

:

Die Impulsantwort des dargestellten Digitalen Filters der Ordnung 3 lautet $\underline{g} = (1, 0, 1, 1)$.

Die Eingangssequenz dieses Filters sei zeitlich unbegrenzt:   $\underline{u} = (1, 1, 0, 0, 0, \ ...)$.

Damit ergibt sich die (unendliche) Ausgangssequenz $\underline{x}$ im binären Galoisfeld ⇒ ${\rm GF(2)}$:

\[\underline{x} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0, \hspace{0.05cm}. ... \hspace{0.05cm}) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1\hspace{0.05cm})= \] \[\hspace{0.3cm} = \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm}0,\hspace{0.05cm} . ... \hspace{0.05cm}) \oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm}0, \hspace{0.05cm} . ... \hspace{0.05cm}) = (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, . ... \hspace{0.05cm}) \hspace{0.05cm}.\]

Bei der herkömmlichen Faltung (für reelle Zahlen) hätte dagegen das Ergebnis gelautet:

\[\underline{x}= (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 1,\hspace{0.05cm} 0, . ... \hspace{0.05cm}) \hspace{0.05cm}.\]

GF(2)–Beschreibungsformen eines Digitalen Filters (2)

Zeitdiskrete Signale kann man auch durch Polynome bezüglich einer Dummy–Variablen repräsentieren.

: Die zum zeitdiskreten Signal $\underline{x} = (x_0, x_1, x_2, \ ...)$ gehörige $\boldsymbol{D}$–Transformierte lautet:

\[X(D) = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \hspace{0.05cm}...\hspace{0.05cm}= \sum_{i = 0}^{\infty} x_i \cdot D^i \hspace{0.05cm}.\]

Für diese spezielle Transformation in einen Bildbereich verwenden wir auch die Notation:

\[\underline{x} = (x_0, x_1, x_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad X(D) = \sum_{i = 0}^{\infty} x_i \cdot D^i \hspace{0.05cm}.\]

In der Literatur wird manchmal $x(D)$ anstelle von $X(D)$ verwendet. Wir schreiben in LNTwww aber alle Bildbereichsfunktionen mit Großbuchstaben, zum Beispiel Fourier–, Laplace– und $D$–Transformation:

\[x(t) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}}\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)\hspace{0.05cm},\hspace{0.4cm} x(t) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\hspace{0.15cm} X(p) \hspace{0.05cm},\hspace{0.4cm} \underline{x} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} X(D) \hspace{0.05cm}.\]

Wir wenden nun die $D$–Transformation auch auf die Informationssequenz $\underline{u}$ und die Impulsantwort $\underline{g}$ an. Aufgrund der zeitlichen Begrenzung von $\underline{g}$ ergibt sich die obere Summationsgrenze bei $G(D)$ zu $i = m$:

\[\underline{u} = (u_0, u_1, u_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = \sum_{i = 0}^{\infty} u_i \cdot D^i \hspace{0.05cm},\]

\[\underline{g} = (g_0, g_1, \hspace{0.05cm}...\hspace{0.05cm}, g_m) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = \sum_{i = 0}^{m} g_i \cdot D^i \hspace{0.05cm}.\]

: Wie bei allen Spektraltransformationen gilt auch bei der $D$–Transformation im Bildbereich die Multiplikation, da die (diskreten) Zeitsignale $\underline{u}$ und $\underline{g}$ durch die Faltung verknüpft sind:

\[\underline{x} = \underline{u} * \underline{g} \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad X(D) = U(D) \cdot G(D) \hspace{0.05cm}.\]

Man bezeichnet, wie in der Systemtheorie allgemein üblich, auch die $D$–Transformierte $G(D)$ der Impulsantwort $\underline{g}$ als Übertragungsfunktion (englisch: Transfer Function).

Der (recht einfache) Beweis dieses wichtigen Ergebnisses finden Sie in der Angabe zu Aufgabe Z3.3.

:

Wir betrachten wieder die zeitdiskreten Signale

\[\underline{u} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D \hspace{0.05cm},\]

\[\underline{g} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D^2 + D^3 \hspace{0.05cm}.\]

Wie im letzten Biespiel: erhält man auch auf diesem Lösungsweg:

\[X(D) \hspace{-0.15cm} = \hspace{-0.15cm} U(D) \cdot G(D) = (1+D) \cdot (1+ D^2 + D^3) =\] \[\hspace{1cm} = \hspace{-0.15cm} 1+ D^2 + D^3 +D + D^3 + D^4 = 1+ D + D^2 + D^4 \]

\[\Rightarrow \hspace{0.4cm} \underline{x} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, ... \hspace{0.05cm}) \hspace{0.05cm}.\]

Die Multiplikation mit $D$ im Bildbereich entspricht im Zeitbereich einer Verschiebung um eine Stelle nach rechts, weshalb man $D$ als Verzögerungsoperator (englisch: Delay Operator) bezeichnet:

\[W(D) = D \cdot X(D) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\circ\quad \underline{w} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, ... \hspace{0.05cm}) \hspace{0.05cm}.\]

Anwendung der D–Transformation auf Rate–1/n–Faltungscoder (1)

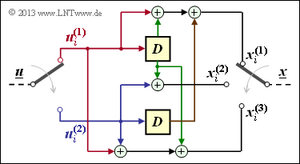
Wir wenden nun die Ergebnisse der letzten Seite auf einen Faltungscoder an, wobei wir uns zunächst auf den Sonderfall k = 1 beschränken. Ein solcher (n, k = 1)–Faltungscode lässt sich mit n Digitalen Filtern realisieren, die auf der gleichen Informationssequenz u parallel arbeiten. Die Grafik zeigt die Anordnung für den Codeparameter n = 2  ⇒  Coderate R = 1/2.

Die nachfolgenden Gleichungen gelten für beide Filter gleichermaßen, wobei für das obere Filter j = 1 und für das untere Filter j = 2 zu setzen ist:

• Die Impulsantworten der beiden Filter ergeben sich zu

\[\underline{g}^{(j)} = (g_0^{(j)}, g_1^{(j)}, \hspace{0.05cm}...\hspace{0.05cm}, g_m^{(j)}\hspace{0.01cm}) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]

• Die beiden Ausgangssequenzen lauten:

\[\underline{x}^{(j)} = (x_0^{(j)}, x_1^{(j)}, x_2^{(j)}, \hspace{0.05cm}...\hspace{0.05cm}) = \underline{u} \cdot \underline{g}^{(j)} \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]

Hierbei ist berücksichtigt, dass das obere Filter und das untere Filter beide auf der gleichen Eingangssequenz u = (u₀, u₁, u₂, ...) arbeiten.

• Für die D–Transformierten der Ausgangssequenzen gilt:

\[X^{(j)}(D) = U(D) \cdot G^{(j)}(D) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]

Auf der nächsten Seite verwenden wir eine kompaktere Schreibweise.

Anwendung der D–Transformation auf Rate–1/n–Faltungscoder (2)

Um den soeben dargelegten Sachverhalt kompakter darstellen zu können, definieren wir nun folgende vektorielle Größen eines Faltungscodes der Rate 1/n:

: Die D–Übertragungsfunktionen der n parallel angeordneten digitalen Filter werden im Vektor G(D) zusammengefasst:

\[\underline{G}(D) = \left ( G^{(1)}(D), G^{(2)}(D), \hspace{0.05cm}...\hspace{0.1cm}, G^{(n)} (D) \right )\hspace{0.05cm}.\]

Der Vektor X(D) beinhaltet die D–Transformierten der n Codesequenzen x⁽¹⁾, x⁽²⁾, ... , x⁽ⁿ⁾:

\[\underline{X}(D) = \left ( X^{(1)}(D), X^{(2)}(D), \hspace{0.05cm}...\hspace{0.1cm}, X^{(n)} (D) \right )\hspace{0.05cm}.\]

Damit erhält man die folgende Vektorgleichung:

\[\underline{X}(D) = U(D) \cdot \underline{G}(D)\hspace{0.05cm}.\]

Aufgrund des Codeparameters k = 1 ist U(D) hier keine vektorielle Größe.

:

Wir betrachten beispielhaft den skizzierten Faltungscode mit den Codeparametern n = 2, k = 1 und m = 2. Für diesen gilt:

\[\underline{g}^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D + D^2 \hspace{0.05cm},\] \[\underline{g}^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D^2 \]

\[\Rightarrow \hspace{0.3cm} \underline{G}(D) = \big ( 1+ D + D^2 \hspace{0.05cm}, \hspace{0.1cm}1+ D^2 \big )\hspace{0.05cm}.\]

Die Informationssequenz sei u = (1, 0, 1, 1), was zur D–Transformierten U(D) = 1 + D² + D³ führt. Damit erhält man

\[\underline{X}(D) = \left ( X^{(1)}(D),\hspace{0.1cm} X^{(2)}(D) \right ) = U(D) \cdot \underline{G}(D) \hspace{0.05cm}, \hspace{0.2cm}\]

wobei

\[{X}^{(1)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (1+ D^2 + D^3) \cdot (1+ D + D^2)=\] \[\hspace{1.5cm} = \hspace{-0.15cm}1+ D + D^2 + D^2 + D^3 + D^4 + D^3 + D^4 + D^5 = 1+ D + D^5\]

\[\Rightarrow \underline{x}^{(1)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} ... \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm},\]

\[{X}^{(2)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (1+ D^2 + D^3) \cdot (1+ D^2)=\] \[\hspace{1.5cm} = \hspace{-0.15cm}1+ D^2 + D^2 + D^4 + D^3 + D^5 = 1+ D^3 + D^4 + D^5\]

\[\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} ... \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm}.\]

Das gleiche Ergebnis haben wir in der Aufgabe Z3.1 auf anderem Wege erhalten. Nach dem Multplexen der beiden Sränge erhält man wieder:   x = (11, 10, 00, 01, 01, 11, 00, 00, ... ).

Übertragungsfunktionsmatrix – Transfer Function Matrix (1)

Auf der letzten Seite haben wir gesehen, dass ein Faltungscode der Rate 1/n sich am kompaktesten als Vektorgleichung im D–transformierten Bereich beschreiben lässt:

\[\underline{X}(D) = U(D) \cdot \underline{G}(D)\hspace{0.05cm}.\]

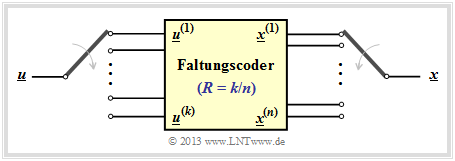
Nun erweitern wir das Resultat auf Faltungscodierer mit mehr als einem Eingang  ⇒  k≥ 2 (siehe Grafik).

Um einen Faltungscode der Rate k/n im D–Bereich abbilden zu können, muss die Dimension obiger Vektorgleichung hinsichtlich Eingang und Übertragungsfunktion erhöht werden:

\[\underline{X}(D) = \underline{U}(D) \cdot { \boldsymbol{\rm G}}(D)\hspace{0.05cm},\]

mit folgenden Maßnahmen:

• Aus der skalaren Funktion U(D) wird der Vektor U(D) = (U⁽¹⁾(D), U⁽²⁾(D), ... , U^(k)(D)).
  

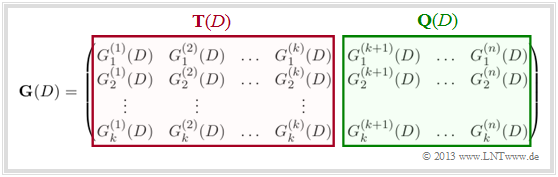
• Aus dem Vektor G(D) wird die k×n–Matrix G(D), die man als Übertragungsfunktionsmatrix bezeichnet (englisch: Transfer Function Matrix oder auch Polynomial Generator Matrix):

\[{\boldsymbol{\rm G}}(D)=\begin{pmatrix} G_1^{(1)}(D) & G_1^{(2)}(D) & \ldots & G_1^{(n)}(D)\\ G_2^{(1)}(D) & G_2^{(2)}(D) & \ldots & G_2^{(n)}(D)\\ \vdots & \vdots & & \vdots\\ G_k^{(1)}(D) & G_k^{(2)}(D) & \ldots & G_k^{(n)}(D) \end{pmatrix}\hspace{0.05cm}.\]

• Jedes der k·n Matrixelemente G_i^(j)(D) mit 1 ≤ i ≤ k, 1 ≤ j ≤ n ist ein Polynom über der Dummy–Variablen D im Galoisfeld GF(2), maximal vom Grad m, wobei m das Gedächtnis angibt.
  

• Für die obige Übertragungsfunktionsmatrix kann mit den zu Beginn dieses Kapitels definierten Teilmatrizen G₀, ... , G_m auch geschrieben werden (als Index verwenden wir wieder l):

\[{\boldsymbol{\rm G}}(D) = \sum_{l = 0}^{m} {\boldsymbol{\rm G}}_l \cdot D\hspace{0.03cm}^l = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D + {\boldsymbol{\rm G}}_2 \cdot D^2 + ... \hspace{0.05cm}+ {\boldsymbol{\rm G}}_m \cdot D\hspace{0.03cm}^m \hspace{0.05cm}.\]

Auf der nächsten Seite werden diese Definitionen und Gesetzmäßigkeiten an einem ausführlichen Beispiel verdeutlicht.

Übertragungsfunktionsmatrix – Transfer Function Matrix (2)

:

Wir betrachten nun wieder den (n = 3, k = 2, m = 1)–Faltungscoder, dessen Teilmatrizen in einem früheren Beispiel wie folgt ermittelt wurden:

\[{ \boldsymbol{\rm G}}_0 = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}, \\ { \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 & 1 & 1\\ 1 & 0 & 0 \end{pmatrix}\hspace{0.05cm}.\]

Wegen m = 1 existieren keine Teilmatrizen für l ≥ 2. Damit lautet die Übertragungsfunktionsmatrix:

\[{\boldsymbol{\rm G}}(D) = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D = \begin{pmatrix} 1+D & D & 1+D\\ D & 1 & 1 \end{pmatrix} \hspace{0.05cm}.\]

Die (zeitlich begrenzte) Informationssequenz sei u = (0, 1, 1, 0, 0, 0, 1, 1), woraus sich die beiden Eingangsfolgen wie folgt ergeben:

\[\underline{u}^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad {U}^{(1)}(D) = D + D^3 \hspace{0.05cm},\] \[\underline{u}^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad {U}^{(2)}(D) = 1 + D^3 \hspace{0.05cm}.\]

Daraus folgt für den Vektor der D–Transformierten am Coderausgang:

\[\underline{X}(D) \hspace{-0.15cm} = \hspace{-0.15cm} \big (\hspace{0.05cm} {X}^{(1)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(2)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(3)}(D)\hspace{0.05cm}\big ) = \underline{U}(D) \cdot {\boldsymbol{\rm G}}(D)\] \[\hspace{1cm} = \hspace{-0.15cm} \begin{pmatrix} D+D^3 & 1+D^3 \end{pmatrix} \cdot \begin{pmatrix} 1+D & D & 1+D\\ D & 1 & 1 \end{pmatrix}\hspace{0.05cm}.\]

Damit ergeben sich in den drei Strängen folgende Codesquenzen:

\[{X}^{(1)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot (1+D) + (1 + D^3) \cdot D =\] \[\hspace{1.5cm} = \hspace{-0.15cm} D + D^2 + D^3 + D^4 + D + D^4 = D^2 + D^3\]

\[\Rightarrow \underline{x}^{(1)} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm},\]

\[{X}^{(2)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot D + (1 + D^3) \cdot 1 =\] \[\hspace{1.5cm} = \hspace{-0.15cm} D^2 + D^4 + 1 + D^3 = 1+D^2 + D^3 + D^4\]

\[\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm},\]

\[{X}^{(3)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot (1 + D) + (1 + D^3) \cdot 1 =\] \[\hspace{1.5cm} = \hspace{-0.15cm} D + D^2 + D^3+ D^4 + 1 + D^3 = 1+ D + D^2 + D^4\]

\[\Rightarrow \underline{x}^{(3)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm}.\]

Die gleichen Ergebnisse haben wir auf anderen Wegen bereits in vorherigen Beispielen erhalten:

• im Beispiel von Kapitel 3.1, Seite 4.
  

• im Beispiel von Kapitel 3.2, Seite 2.

Systematische Faltungscodes (1)

Die Polynomrepräsentation anhand der Übertragungsfunktionsmtrix G(D) ermöglicht Einblicke in die Struktur eines Faltungscodes. Beispielsweise erkennt man anhand dieser k&timesn–Matrix, ob es sich um einen systematischen Code handelt. Darunter versteht man einen Code, bei dem die Codesequenzen x⁽¹⁾, ... , x^(k) mit den Informationssequenzen u⁽¹⁾, ... , u^(k) identisch sind. Die Grafik zeigt beispielhaft einen systematischen (n = 4, k = 3)–Faltungscode.

Ein systematischer (n, k)–Faltungscode liegt immer dann vor, wenn die Übertragungsfunktionsmatrix (mit k Zeilen und n Spalten) folgendes Aussehen hat:

\[{\boldsymbol{\rm G}}(D) = {\boldsymbol{\rm G}}_{\rm sys}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\big ] \hspace{0.05cm}.\]

Hierbei ist folgende Nomenklatur verwendet:

• I_k bezeichnet eine diagonale Einheitsmatrix der Dimension k × k.
  

• P(D) ist eine k × (n –k)–Matrix, wobei jedes Matrixelement ein Polynom in D beschreibt.
  
  

: Ein systematischer Faltungscode mit den Codeparametern n = 3, k = 2, m = 2 könnte beispielsweise die folgende Übertragungsfunktionsmatrix aufweisen:

\[{\boldsymbol{\rm G}}_{\rm sys}(D) = \begin{pmatrix} 1 & 0 & 1+D^2\\ 0 & 1 & 1+D \end{pmatrix}\hspace{0.05cm}.\]

Andere systematische Faltungscodes mit gleichem n und gleichem k unterscheiden sich demgegenüber nur durch die beiden Matrixelemente in der letzten Spalte.

Zu jedem (n, k)–Faltungscode mit der Generatormatrix G(D) kann ein äquivalenter systematischer Code gefunden werden, dessen D–Matrix wir mit G_sys(D) benennen.

Auf der nächsten Seite wird gezeigt, wie man von einer beliebigen Matrix G(D) durch Aufspalten in zwei Teilmatrizen T(D) und Q(D) und verschiedene Matrizenoperationen zur Matrix G_sys(D) kommt.

Systematische Faltungscodes (2)

Um von einer Übertragungsfunktionsmatrix G(D) zur Matrix G_sys(D) eines äquivalenten systematischen Faltungscodes zu kommen, geht man entsprechend der Grafik auf der letzten Seite wie folgt vor:

• Man unterteilt die k×n–Matrix G(D) in eine quadratische Matrix T(D) mit k Zeilen und k Spalten und bezeichnet den Rest mit Q(D).

• Anschließend berechnet man die zu T(D) inverse Matrix T^–1(D) und daraus die Matrix für den äquivanten systematischen Code:

\[{\boldsymbol{\rm G}}_{\rm sys}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm G}}(D) \hspace{0.05cm}.\]

• Da T^–1(D) · T(D) die k×k–Einheitsmatrix I_k ergibt, kann die Übertragungsfunktionsmatrix des äquivalenten systematischen Codes in der gewünschten Form geschrieben werden:

\[{\boldsymbol{\rm G}}_{\rm sys}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\big ] \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\boldsymbol{\rm P}}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D) \hspace{0.05cm}. \hspace{0.05cm}\]

:

Der auf den letzten Seiten schon häufiger betrachtete Coder der Rate 2/3 ist nicht systematisch, weil zum Beispiel

x⁽¹⁾ ≠ u⁽¹⁾, x⁽²⁾ ≠ u⁽²⁾ gilt (siehe nebenstehende Coderschaltung).

Man erkennt dies aber auch anhand der Übertragungsfunktionsmatrix:

\[{\boldsymbol{\rm G}}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm T}}(D)\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm Q}}(D) \hspace{0.05cm}\big ]\]

\[\Rightarrow \hspace{0.3cm} {\boldsymbol{\rm T}}(D) = \begin{pmatrix} 1+D & D\\ D & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.2cm} {\boldsymbol{\rm Q}}(D) = \begin{pmatrix} 1+D \\ 1 \end{pmatrix}\hspace{0.05cm}.\]

Die Determinante von T(D) ergibt sich zu (1 + D) · 1 + D · D = 1 + D + D² und ist ungleich 0. Somit kann für die Inverse von T(D) geschrieben werden (Vertauschung der Diagonalelemente!):

\[{\boldsymbol{\rm T}}^{-1}(D) = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} 1 & D\\ D & 1+D \end{pmatrix}\hspace{0.05cm}.\]

Das Produkt T(D) · T^–1(D) ergibt die Einheitsmatrix I₂, und für die dritte Spalte von G_sys(D) gilt:

\[{\boldsymbol{\rm P}}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D) = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} 1 & D\\ D & 1+D \end{pmatrix}\cdot \begin{pmatrix} 1+D\\ 1 \end{pmatrix} \]

\[\Rightarrow \hspace{0.3cm} {\boldsymbol{\rm P}}(D) = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} (1+D) + D \\ D \cdot (1+D) + (1+D) \end{pmatrix} = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} 1 \\ 1+D^2 \end{pmatrix} \]

\[\Rightarrow \hspace{0.2cm}{\boldsymbol{\rm G}}_{\rm sys}(D) = \begin{pmatrix} 1 & 0 & \frac{1}{1+D+D^2}\\ 0 & 1 &\frac{1+D^2}{1+D+D^2} \end{pmatrix}\hspace{0.05cm}. \]

Es ist noch zu klären, wie das Filter einer solchen gebrochen–rationalen Übertragungsfunktion aussieht.

Filterstruktur bei gebrochen–rationaler Übertragungsfunktion

Hat eine Übertragungsfunktion die Form G(D) = A(D)/B(D), so bezeichnet man das zugehörige Filter als rekursiv. Bei einem rekursiven Faltungscodierer mit dem Gedächtnis m kann für die beiden Polynome A(D) und B(D) allgemein geschrieben werden:

\[A(D) \hspace{-0.15cm} = \hspace{-0.15cm} \sum_{l = 0}^{m} a_l \cdot D^l = a_0 + a_1 \cdot D + a_2 \cdot D^2 + ... \hspace{0.05cm} + a_m \cdot D^m \hspace{0.05cm},\] \[B(D) \hspace{-0.15cm} = \hspace{-0.15cm} 1 + \sum_{l = 1}^{m} b_l \cdot D^l = 1 + b_1 \cdot D + b_2 \cdot D^2 + ... \hspace{0.05cm} + b_m \cdot D^m \hspace{0.05cm}.\]

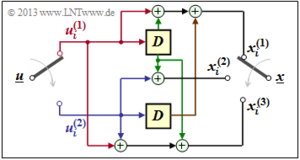
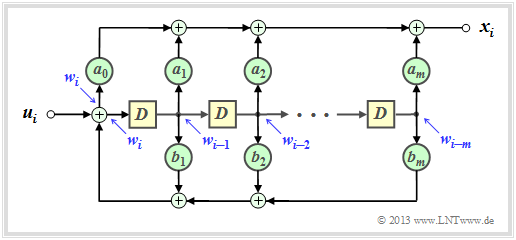
Die Grafik zeigt die entsprechende Filterstruktur in der so genannten Controller Canonical Form.

Die Koeffizienten a₀, ... , a_m beschreiben den Vorwärtszweig, während b₁, ... , b_m eine Rückkopplung bilden. Alle Koeffizienten sind binär, also 1 (durchgehende Verbindung) oder 0 (fehlende Verbindung).

: Die rechts skizzierte Filterstruktur lässt sich durch folgende Gleichungen beschreiben:

\[x_i \hspace{-0.15cm} = \hspace{-0.15cm} w_i + w_{i-2} \hspace{0.05cm},\] \[w_i \hspace{-0.15cm} = \hspace{-0.15cm} u_i + w_{i-1}+ w_{i-2} \hspace{0.05cm}.\]

Entsprechend gilt für die D–Transformierten:

\[X(D) \hspace{0.15cm} = \hspace{0.15cm} W(D) + W(D) \cdot D^2 =\] \[ \hspace{1.3cm} = \hspace{0.15cm} W(D) \cdot \left ( 1+ D^2 \right ) \hspace{0.05cm},\]

\[W(D) = \hspace{0.08cm} U(D) + W(D) \cdot D+ W(D) \cdot D^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} U(D) = W(D) \cdot \left ( 1+ D + D^2 \right ) \hspace{0.05cm}.\]

Somit erhält man für die Übertragungsfunktion dieses Filters:

\[G(D) = \frac{X(D)}{U(D)} = \frac{1+D^2}{1+D+D^2} \hspace{0.05cm}. \]

Im Beispiel zu den systematischen Faltungscodes hat sich genau ein solcher Ausdruck ergeben.

Aufgaben

A3.2 G–Matrix eines Faltungscoders

A3.3 x über U(D) und G(D)

A3.4 Systematische Faltungscodes

A3.5 Rekursive Filter für GF(2)