Aufgabe 2.1Z: Summensignal

• Zurück zum Buch

Rechtecksignal, Dreiecksignal und Summensignal

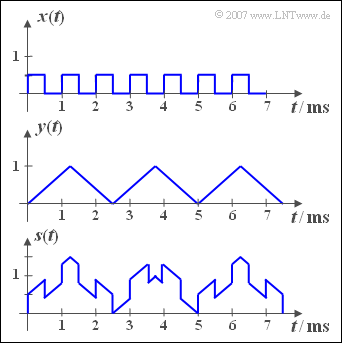
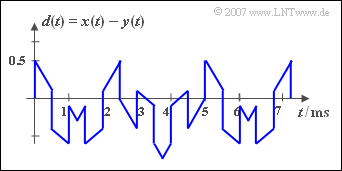
In der nebenstehenden Grafik sind die beiden periodischen Signale ${x(t)}$ und ${y(t)}$ dargestellt, aus denen das Summensignal ${s(t)}$ – im unteren Bild skizziert – sowie das Differenzsignal ${d(t)}$ gebildet werden.

Weiterhin betrachten wir in dieser Aufgabe das Signal ${w(t)}$, das sich aus der Summe der beiden periodischen Signalen ${u(t)}$ und $v(t)$ ergibt. Die Grundfrequenzen der Signale seien

• $f_u = 998 \,\text{Hz},$

• $f_v = 1002 \,\text{Hz}.$

Mehr ist von diesen Signalen ${u(t)}$ und $v(t)$ nicht bekannt.

Hinweis:

• Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung periodischer Signale.

Fragebogen

1

Wie groß ist Periodendauer $T_x$ und Grundfrequenz $f_x$ des Signals ${x(t)}$?

$f_x\ = \ $   $\text{kHz}$

2

Wie groß ist Periodendauer $T_y$ und Grundfrequenz $f_y$ des Signals ${y(t)}$?

$f_y\ = \ $   $\text{kHz}$

3

Bestimmen Sie die Grundfrequenz $f_s$ sowie die Periodendauer $T_s$ des Summensignals ${s(t)}$ und überprüfen Sie das Ergebnis anhand der Skizze.

$T_s\ = \ $   $\text{ms}$

4

Welche Periodendauer $T_d$ weist das Differenzsignal ${d(t)}$ auf?

$T_d\ = \ $   $\text{ms}$

5

Welche Periodendauer $T_w$ besitzt das Signal ${w(t)} = {u(t)} + v(t)$?

$T_w\ = \ $   $\text{ms}$

Musterlösung

Musterlösung

(1)  Für das Rechtecksignal gilt $T_x = 1 \,\text{ms}$   ⇒   $f_x \hspace{0.15cm}\underline{= 1 \, \text{kHz}}$.

(2)  Für das Dreiecksignal gilt $T_y = 2.5 \,\text{ms}$ und $f_y \hspace{0.15cm}\underline{= 0.4\, \text{kHz}}$.

(3)  Die Grundfrequenz $f_s$ des Summensignals $s(t)$ ist der größte gemeinsame Teiler von $f_x = 1 \,\text{kHz}$ und $f_y = 0.4 \,\text{kHz}$. Daraus folgt $f_s = 200 \,\text{Hz}$ und die Periodendauer $T_s\hspace{0.15cm}\underline{ = 5 \,\text{ms}}$, wie auch aus der grafischen Darstellung des Signals ${s(t)}$ auf der Angabenseite hervorgeht.

Differenzsignal $d(t) = x(t) - y(t)$

(4)  Die Periodendauer $T_d$ ändert sich gegenüber der Periodendauer $T_s$ nicht, wenn das Signal ${y(t)}$ nicht addiert, sondern subtrahiert wird:     $T_d = T_s \hspace{0.15cm}\underline{= 5\, \text{ms}}$.

(5)  Der größte gemeinsame Teiler von $f_u = 998 \,\text{Hz}$ und $f_{v} = 1002 \,\text{Hz}$ ist $f_w = 2 \,\text{Hz}$. Der Kehrwert hiervon ergibt die Periodendauer $T_w \hspace{0.15cm}\underline{= 500 \,\text{ms}}$.