Berücksichtigung von Kanalverzerrungen und Entzerrung

Inhaltsverzeichnis

1 Idealer Kanalentzerrer
2 Erhöhung der Rauschleistung durch lineare Entzerrung
3 Optimierung der Grenzfrequenz
4 Optimale Grenzfrequenz in Abhängigkeit der Kabeldämpfung
5 Aufgaben zum Kapitel

Idealer Kanalentzerrer

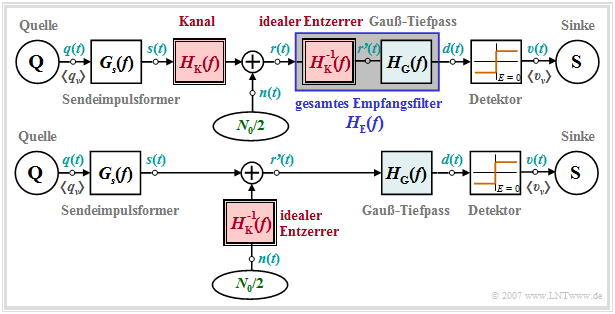
Bei einem Übertragungssystem, dessen Kanalfrequenzgang $H_{\rm K}(f)$ starke Verzerrungen hervorruft, gehen wir von folgendem Blockschaltbild (obere Grafik) und äquivalentem Ersatzschaltbild (untere Grafik) aus.

Block- und Ersatzschaltbild zur Berücksichtigung eines Kanalfrequenzgangs

Zu diesen Darstellungen ist Folgendes anzumerken:

Das Empfangsfilter $H_{\rm E}(f)$ wird – zumindest gedanklich – aus einem idealen Kanalentzerrer $1/H_{\rm K}(f)$ und einem Tiefpass $H_{\rm G}(f)$ zusammengesetzt. Für Letzteren verwenden wir in diesem Kapitel beispielhaft einen Gaußtiefpass mit der Grenzfrequenz $f_{\rm G}$.

Verschiebt man nun den idealen Entzerrer – wiederum rein gedanklich – auf die linke Seite der Rauschadditionsstelle, so ändert sich bezüglich dem S/N–Verhältnis an der Sinke und bezüglich der Fehlerwahrscheinlichkeit nichts gegenüber dem oben gezeichneten Blockschaltbild.

Aus dem unteren Ersatzschaltbild erkennt man, dass sich durch den Kanalfrequenzgang $H_{\rm K}(f)$ auch bezüglich des Detektionsnutzsignals $d_{\rm S}(t)$ – herrührend vom Sendesignal $s(t)$ – nichts ändert, wenn man diesen mit $1/H_{\rm K}(f)$ vollständig kompensiert. Das Nutzsignal hat somit die genau gleiche Form wie im Kapitel Fehlerwahrscheinlichkeit unter Berücksichtigung von Impulsinterferenzen berechnet.

Die Degradation durch den Kanalfrequenzgang $H_{\rm K}(f)$ zeigt sich vielmehr durch eine signifikante Erhöhung der Detektionsstörleistung, also der Varianz des Signals $d_{\rm N}(t)$ – herrührend vom Störsignal $n(t)$:

$$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} \frac{1}{|H_{\rm K}(f)|^2}\cdot |H_{\rm G}(f)|^2 \,{\rm d} f \hspace{0.05cm}.$$

Voraussetzung für eine endliche Störleistung $\sigma_d^2$ ist, dass der Tiefpass $H_{\rm G}(f)$ das Rauschen $n(t)$ bei (sehr) hohen Frequenzen stärker abschwächt, als es vom idealen Entzerrer $1/H_{\rm K}(f)$ angehoben wird.

Anmerkung: Der Kanalfrequenzgang $H_{\rm K}(f)$ ist nach Betrag und Phase zu entzerren, allerdings nur in einem von $H_{\rm G}(f)$ vorgegebenen eingeschränkten Frequenzbereich. Eine vollständige Phasenentzerrung ist aber nur auf Kosten einer (frequenzunabhängigen) Laufzeit möglich, die im Folgenden nicht weiter berücksichtigt wird.

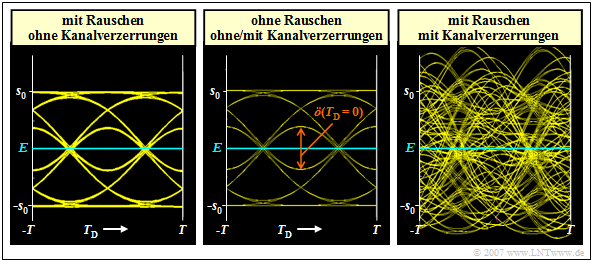
$\text{Beispiel 1:}$ Wir betrachten wieder ein Binärsystem mit NRZ–Rechteckimpulsen und gaußförmigem Empfangsfilter $H_{\rm E}(f) = H_{\rm G}(f)$ mit der (normierten) Grenzfrequenz $f_\text{G, opt} \cdot T = 0.4$.

Die mittlere Grafik zeigt für diesen Fall das Augendiagramm des Detektionsnutzsignals $d_{\rm S}(t)$ – also ohne Berücksichtigung des Rauschens.
Dieses ist identisch mit dem im Kapitel Definition und Aussagen des Augendiagramms im $\text{Beispiel 3}$ (rechte Grafik) dargestellten Augendiagramm.

Binäre Augendiagramme mit Impulsinterferenzen

Das linke Augendiagramm ergibt sich bei idealem Kanal, also für $H_{\rm K}(f) = 1$ ⇒ $1/H_{\rm K}(f) = 1$. Es berücksichtigt das AWGN–Rauschen, das aber hier mit $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 30 \ \rm dB$ als sehr klein angenommen wurde. Für diese Konfiguration wurde per Simulation ermittelt:

$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\approx 26.8\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}< 10^{-40}\hspace{0.05cm}.$$

Dagegen gilt das rechte Diagramm für ein Koaxialkabel, wobei die charakteristische Kabeldämpfung $a_\star = 40 \ \rm dB$ beträgt. Hierfür ergeben sich bei gleichem $E_{\rm B}/N_0$ deutlich ungünstigere Systemgrößen:

$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\approx -4.6\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}\approx 0.28\hspace{0.05cm}.$$

Dieses Ergebnis kann wie folgt interpretiert werden:

Unter der Voraussetzung eines idealen Kanalentzerrers $1/H_{\rm K}(f)$ ergibt sich auch beim verzerrenden Kanal das gleiche „Augendiagramm ohne Rauschen” (linke Grafik) wie beim idealen Kanal $H_{\rm K}(f) = 1$ (mittlere Grafik).

Durch die Kanalentzerrung $1/H_{\rm K}(f)$ wird der Rauschanteil extrem verstärkt. Im rechten Beispiel ist wegen der starken Verzerrung eine ebenso starke Entzerrung über einen weiten Frequenzbereich erforderlich.
Die Rauschleistung $\sigma_d^2$ ist hier um den Faktor $1300$ größer als bei der linken Konstellation (keine Verzerrung ⇒ keine Entzerrung). Damit ergibt sich die Fehlerwahrscheinlichkeit zu $p_{\rm S}\approx p_{\rm U}\approx 50 \%$.

Eine akzeptable Fehlerwahrscheinlichkeit ergibt sich nur bei kleinerer Rauschleistungsdichte $N_0$. Beispielsweise erhält man mit mit $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 50 \ \rm dB$ $($statt $30 \ \rm dB)$ das folgende Ergebnis:

$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = -4.6 +20 \approx 15.4\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}\approx 2 \cdot 10^{-9} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} \ge p_{\rm U}/4 \approx 0.5 \cdot 10^{-9}\hspace{0.05cm}.$$

Erhöhung der Rauschleistung durch lineare Entzerrung

Die Augendiagramme auf der letzten Seite dokumentieren eindrucksvoll die Erhöhung der Rauschleistung $\sigma_d^2$ bei unveränderter vertikaler Augenöffnung, wenn man den Kanalfrequenzgang $H_{\rm K}(f)$ empfangsseitig durch dessen Inverse kompensiert. Dieses Ergebnis soll nun anhand der Rauschleistungsdichte ${\it \Phi}_{d{\rm N}}(f)$ nach dem Empfangsfilter (vor dem Entscheider) interpretiert werden, wobei folgende Einstellungen gelten:

Der Kanal sei ein Koaxialkabel mit dem Betragsfrequenzgang

$$|H_{\rm K}(f)| = {\rm exp}\left [- a_{\star}\cdot \sqrt{2 f T}\hspace{0.05cm} \right ]\hspace{0.2cm}{\rm mit}\hspace{0.2cm} a_{\star} = 1.7\,\,{\rm Np}\hspace{0.2cm} ({\rm entsprechend} \hspace{0.2cm} 15\,\,{\rm dB}) \hspace{0.05cm}.$$

Der ideale Kanalentzerrer $1/H_{\rm K}(f)$ kompensiert den Kanalfrequenzgang vollständig. Über die Realisierung der Dämpfungs– und Phasenentzerrung wird hier keine Aussage getroffen.

Zur Rauschleistungsbegrenzung wird ein Gaußtiefpass eingesetzt:

$$|H_{\rm G}(f)| = {\rm exp}\left [- \pi \cdot \left (\frac{f }{2 f_{\rm G}}\right )^2 \right ]\hspace{0.2cm}{\rm mit}\hspace{0.2cm} f_{\rm G} = 0.8/T \hspace{0.2cm} {\rm bzw.} \hspace{0.2cm} f_{\rm G} = 0.4/T \hspace{0.05cm}.$$

Damit gilt für die Rauschleistungsdichte vor dem Entscheider:

$${\it \Phi}_{d{\rm N}}(f) = \frac{N_0}{2} \cdot \frac{|H_{\rm G }(f)|^2}{|H_{\rm K}(f)|^2} = \frac{N_0}{2} \cdot {\rm exp}\left [2 \cdot a_{\star}\cdot \sqrt{2 f T} - {\pi}/{2} \cdot \left ({f }/{f_{\rm G}}\right )^2 \right ] \hspace{0.05cm}.$$

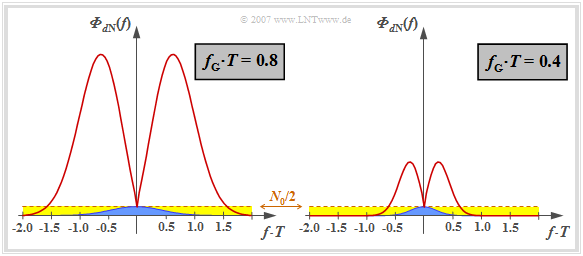
Rauschüberhöhung durch verzerrenden Kanal

Dieser Verlauf ist nebenstehend dargestellt für die beiden (normierten) Grenzfrequenzen

$f_\text{G} \cdot T = 0.8$ (links) bzw.
$f_\text{G} \cdot T = 0.4$ (rechts)

Beachten Sie, dass hier aus Darstellungsgründen die charakteristische Kabeldämpfung mit $a_\star = 15 \ \rm dB$ $($entsprechend $1.7 \ \rm Np)$ deutlich kleiner gewählt ist als beim rechten Augendiagramm im $\text{Beispiel 1}$ auf der letzten Seite $($gültig für $a_\star = 40 \ \rm dB)$.
Betrachten wir zunächst die linke Grafik für die (normierte) Grenzfrequenz $f_\text{G} \cdot T = 0.8$, die nach den Berechnungen im letzten Kapitel für den idealen Kanal ⇒ $H_{\rm K}(f) = 1$ das Optimum darstellt.

Gelb hinterlegt ist die konstante Rauschleistungsdichte $N_0/2$ am Empfängereingang. Bei idealem Kanal wird diese durch das gaußförmige Empfangsfilter $H_{\rm E}(f) = H_{\rm G}(f)$ begrenzt und ergibt die Detektionsrauschleistung $\sigma_d^2$ (in der Grafik durch die blaue Fläche gekennzeichnet).

Werden – wie bei leitungsgebundener Übertragung üblich – höhere Frequenzen stark gedämpft, so steigt $|H_{\rm E}(f)| = |H_{\rm G}(f)|/|H_{\rm K}(f)|$ aufgrund des idealen Kanalentzerrers sehr stark an, bevor für $f \cdot T \ge 0.6$ $($nur gültig für $a_\star = 15 \ \rm dB$ und $f_\text{G} \cdot T = 0.8)$ der dämpfende Einfluss des Gaußfilters wirksam wird.

Die Rauschleistung $\sigma_d^2$ ist nun gleich der Fläche unter der roten Kurve, die etwa um den Faktor $28$ größer ist als die blaue Fläche. Die Auswirkungen dieser unterschiedlichen Rauschleistungen erkennt man auch in den Augendiagrammen auf der letzten Seite, allerdings für $a_\star = 40 \ \rm dB$.

Die rechte Grafik zeigt die Rauschleistungsdichte ${\it \Phi}_{d{\rm N}}(f)$ für die normierte Grenzfrequenz $f_\text{G} \cdot T = 0.4$. Hier wird die Rauschleistung durch den idealen Kanalentzerrer nur noch um den Faktor $9$ vergrößert (Verhältnis zwischen der Fläche unter der roten Kurve und der blauen Fläche).

$\text{Fazit:}$ Aus obiger Grafik und den bisherigen Erläuterungen geht bereits hervor, dass bei verzerrendem Kanal ⇒ $H_{\rm K}(f) \ne 1$ die Grenzfrequenz $f_\text{G} \cdot T = 0.8$ des Gaußtiefpasses $H_{\rm G}(f)$ nach dem idealen Kanalentzerrer $1/H_{\rm K}(f)$ nicht mehr optimal sein wird.

Optimierung der Grenzfrequenz

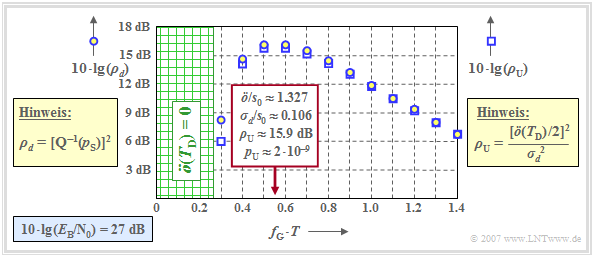
Die Grafik zeigt die Störabstände in Abhängigkeit der Grenzfrequenz $f_{\rm G}$ des gaußförmigen Gesamtfrequenzgangs $H_{\rm G}(f) = H_{\rm K}(f) \cdot H_{\rm E}(f)$. Dieses Bild gilt für

einen koaxialen Übertragungskanal mit der charakteristischen Kabeldämpfung $a_\star = 15 \ \rm dB$,
AWGN–Rauschen mit $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 27 \ \rm dB$, wobei $E_{\rm B} = s_0^2 \cdot T$ zu setzen ist ⇒ NRZ–Rechteckimpulse.

Optimale Grenzfrequenz des GTP bei verzerrendem Kanal $(a_\star = 15 \ \rm dB)$

Anmerkungen:

Die Kreise zeigen die dB–Werte für $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d$ ⇒ „mittleres” Detektions–SNR (Maß für die mittlere Fehlerwahrscheinlichkeit $p_{\rm S})$.
Die Quadrate zeigen die dB–Werte für $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U}$ ⇒ „ungünstigstes” SNR $($Maß für die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U})$.

Man erkennt aus dieser Darstellung und durch Vergleich mit der entsprechenden Grafik im letzten Kapitel, die für $H_{\rm K}(f) = 1$ und $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 13 \ \rm dB$ gegolten hat:

Auch bei stark verzerrendem Kanal ist $\rho_{\rm U}$ eine geeignete untere Schranke für $\rho_d$ ⇒ $\rho_{d} \ge \rho_{\rm U}$. Entsprechend ist auch $p_{\rm U} \ge p_{\rm S} $ eine sinnvolle obere Schranke für $p_{\rm S}$.

Bei der betrachteten Kabeldämpfung $a_\star = 15 \ \rm dB$ ist die Grenzfrequenz $f_\text{G} \cdot T \approx 0.55$ optimal und es gilt $\ddot{o}/s_0 \approx 1.327$ sowie $\sigma_d/s_0 \approx 0.106$.
Daraus ergeben sich der (ungünstigste) Störabstand $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx \ \rm 15.9 \ dB$ und die Worst–Case–Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2 \cdot 10^{-9}.$

Eine kleinere Grenzfrequenz hätte eine deutlich kleinere Augenöffnung zur Folge, ohne dass dadurch auch $\sigma_d$ gleichermaßen verkleinert würde. Für $f_\text{G} \cdot T = 0.4$ gilt:

$$\ddot{o}/s_0 \approx 0.735,\hspace{0.2cm}\sigma_d/s_0 \approx 0.072\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\approx 14.1\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}\approx 1.8 \cdot 10^{-7}\hspace{0.05cm}.$$

Ist die Grenzfrequenz $f_\text{G}$ zu groß, so wird das Rauschen weniger effektiv begrenzt. Beispielsweise lauten die Werte für die Grenzfrequenz $f_\text{G} \cdot T =0.8$:

$$\ddot{o}/s_0 \approx 1.819,\hspace{0.2cm}\sigma_d/s_0 \approx 0.178\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\approx 14.2\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}\approx 1.7 \cdot 10^{-7}\hspace{0.05cm}.$$

Die optimalen Werte sind mit $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{d} \approx 16.2 \ \rm dB$ und $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx \ \rm 15.9 dB$ deutlich ausgeprägter als bei idealem Kanal.

Bei einem Vergleich der Störabstände ist allerdings zu berücksichtigen, dass hier $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 27 \ \rm dB$ zugrunde liegt; in der entsprechenden Grafik für den idealen Kanal wurde dagegen von $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 13 \ \rm dB$ ausgegangen.

Optimale Grenzfrequenz in Abhängigkeit der Kabeldämpfung

Optimale Grenzfrequenz und Systemwirkungsgrad in Abhängigkeit der charakteristischen Kabeldämpfung. Insbesondere gilt:
$\hspace{0.8cm} 10 · \lg \eta\hspace{0.05cm}(a_\star = 0 \ \rm dB) = -1.4 \ dB;$ $\hspace{0.8cm} 10 · \lg \eta\hspace{0.05cm}(a_\star = 80 \ \rm dB) = -78.2 \ dB;$

Wir betrachten weiter

ein Binärsystem mit NRZ–Sendeimpulsen ⇒ $E_{\rm B} = s_0^2 \cdot T$,
ein Koaxialkabel $H_{\rm K}(f)$, charakteristische Dämpfung $a_\star$,
einen Gauß–Gesamtfrequenzgang $H_{\rm G}(f) = H_{\rm K}(f) \cdot H_{\rm E}(f)$.

Die blauen Kreise (linke Achsenbeschriftung) markieren die optimale Grenzfrequenzen $f_\text{G, opt}$ für die jeweilige Kabeldämpfung $a_\star$.

Zusätzlich ist in der Grafik mit roten Quadraten der Systemwirkungsgrad (bei Spitzenwertbegrenzung) $\eta$ dargestellt, der das Verhältnis des mit der betrachteten Konfiguration erreichbaren SNR $\rho_{d}$ zum maximal möglichen S/N-Verhältnis $\rho_{d, \ {\rm max}}$ angibt.

Ersetzt man $\rho_d$ durch $\rho_{\rm U}$, also $p_{\rm S}$ durch $p_{\rm U}$, so kann der Systemwirkungsgrad wie folgt dargestellt werden:

$$\eta = \eta_{\rm A}=\frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}|\hspace{0.05cm} A}}}= \frac{\rho_d}{2 \cdot E_{\rm B}/N_0}\approx \frac{\rho_{\rm U}}{2 \cdot E_{\rm B}/N_0}.$$

Man erkennt aus der Anordnung der blauen Kreise:

Die optimale Grenzfrequenz $f_\text{G, opt}$ hängt signifikant ab von der Stärke der Verzerrungen des Koaxialkabels, genauer gesagt: ausschließlich von der charakteristischen Kabeldämpfung $a_\star$ bei der halben Bitrate.
Je größer die Kabeldämpfung $a_\star$ und damit der Rauscheinfluss ist, um so niedriger ist die optimale Grenzfrequenz $f_\text{G, opt}$.
Allerdings ist stets $f_\text{G, opt} > 0.27/T$. Andernfalls wäre das Auge geschlossen, gleichbedeutend mit der „Worst–case”–Fehlerwahrscheinlichkeit $p_{\rm U} = 0.5$.

Diskutieren wir nun die Abhängigkeit des Systemwirkungsgrads $\eta$ (rote Quadrate) von der charakteristischen Kabeldämpfung $a_\star$. Die rechte Ordinate beginnt oben bei $0 \ \rm dB$ und erstreckt sich nach unten bis $-100 \ \rm dB$.

Wie nun an einigen Zahlenbeispielen verdeutlicht werden soll, vermeidet die Darstellung $\eta = \eta\hspace{0.05cm}(a_\star)$ einige Probleme, die sich aus dem großen Wertebereich von S/N–Verhältnissen ergeben:

Der Ordinatenwert $10 \cdot {\rm lg}\hspace{0.1cm} \eta\hspace{0.05cm}(a_\star = 0 \ \rm dB) = -1.4 \ \rm dB$ sagt aus, dass der bei idealem Kanal bestmögliche Gaußtiefpass mit Grenzfrequenz $f_\text{G} \cdot T = 0.8$ um $1.4 \ \rm dB$ schlechter ist als der optimale (Matched–Filter–) Empfänger.

Gehen wir von idealem Kanal $(a_\star = 0 \ \rm dB)$ und $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 10 \ \rm dB$ aus, so besagt die obige Gleichung auch, dass diese Konfiguration zu folgender (worst-case) Fehlerwahrscheinlichkeit führen wird:

$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 10 \cdot {\rm lg}\hspace{0.1cm}{E_{\rm B}}/{N_0} + 10 \cdot {\rm lg}\hspace{0.1cm}(2) + 10 \cdot {\rm lg}\hspace{0.1cm}(\eta) \approx \approx 10\,{\rm dB} \hspace{0.1cm}+\hspace{0.1cm}3\,{\rm dB} \hspace{0.1cm}-\hspace{0.1cm}1.4\, {\rm dB}= 11.6\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U}\approx 7 \cdot 10^{-5}\hspace{0.05cm}.$$

Soll diese (ungünstigste) Fehlerwahrscheinlichkeit $p_{\rm U} = 7 \cdot 10^{-5}$ ⇒ $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} = 11.6 \ \rm dB$ beim Kanal mit der charakteristischen Kabeldämpfung $a_\star = 80 \ \rm dB$ nicht überschritten werden, so muss demnach für das Verhältnis $E_{\rm B}/N_0$ gelten:

\[10 \cdot {\rm lg}\hspace{0.1cm}{E_{\rm B}}/{N_0} \ge 11.6\,{\rm dB} \hspace{0.1cm}-3\,{\rm dB} \hspace{0.1cm}-\hspace{0.1cm}(-78.2)\,{\rm dB}= 86.8\,{\rm dB} \hspace{0.2cm} \Rightarrow \hspace{0.2cm}{E_{\rm B}}/{N_0}\approx 5 \cdot 10^{8}\hspace{0.05cm}.\]

Um dies zu erreichen, muss allerdings die Grenzfrequenz des Gaußtiefpasses entsprechend den blauen Kreisen in der Grafik auf $f_{\rm G}= 0.33/T$ herabgesetzt werden.

Aufgaben zum Kapitel

Aufgabe 3.3: Rauschen bei Kanalentzerrung

Aufgabe 3.3Z: Optimierung eines Koaxialkabelsystems