Aufgabe 5.4: Walsh–Funktionen (PKKF, PAKF)

Hadamard–Matrix ${\mathbf{H}_{8}}$

Häufig verwendet man zur Bandspreizung und Bandstauchung so genannte "Walsh–Funktionen", die mittels der Hadamard–Matrix konstruiert werden können. Ausgehend von der Matrix

$${\mathbf{H}_{2}} = \left[ \begin{array}{ccc} +1 & +1 \\ +1 & -1 \end{array} \right] $$

lassen sich durch folgende Rekursion die weiteren Hadamard–Matrizen $ {\mathbf{H}_{4}}$, $ {\mathbf{H}_{8}}$, usw. herleiten:

$$ {\mathbf{H}_{2J}} = \left[ \begin{array}{ccc} \mathbf{H}_J & \mathbf{H}_J \\ \mathbf{H}_J & -\mathbf{H}_J \end{array} \right] \hspace{0.05cm}.$$

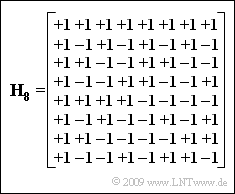
Die Grafik zeigt die Matrix $ {\mathbf{H}_{8}}$ für den Spreizfaktor $J = 8$. Daraus lassen sich die Spreizfolgen

$$ \langle w_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$ \langle w_\nu^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$...$$

$$\langle w_\nu^{(7)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}$$

für sieben CDMA–Teilnehmer ablesen. Die Spreizfolge $ \langle w_\nu^{(0)}\rangle$ entsprechend der ersten Zeile in der Hadamard–Matrix wird meistens nicht vergeben, da sie nicht spreizt.

Die Fragen zu dieser Aufgabe beziehen sich meist auf den Spreizfaktor $J = 4$. Damit können entsprechend mit den Spreizfolgen $ \langle w_\nu^{(1)}\rangle$, $ \langle w_\nu^{(2)}\rangle$ und $ \langle w_\nu^{(3)}\rangle$ maximal drei CDMA–Teilnehmer versorgt werden, die sich aus der zweiten, dritten und vierten Zeile der Matrix $ {\mathbf{H}_{4}}$ ergeben.

Hinsichtlich der Korrelationsfunktionen soll in dieser Aufgabe folgende Nomenklatur gelten:

Die periodische Kreuzkorrelationsfunktion $\rm (PKKF)$ zwischen den Folgen $ \langle w_\nu^{(i)}\rangle$ und $ \langle w_\nu^{(j)}\rangle$ wird mit $φ_{ij}(λ)$ bezeichnet. Hierbei gilt:

$${\it \varphi}_{ij}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(j)} \right ] \hspace{0.05cm}.$$

Ist $φ_{ij} \equiv 0$ $($das heißt: $φ_{ij}(λ) = 0$ für alle Werte von $λ)$, so stören sich die CDMA–Teilnehmer nicht, auch wenn diese unterschiedliche Laufzeiten aufweisen.
Gilt zumindest $φ_{ij}({\it λ} = 0) = 0$, so kommt es zumindest bei synchronem CDMA–Betrieb $($keine oder gleiche Laufzeiten aller Teilnehmer$)$ zu keinen Interferenzen.
Die periodische Autokorrelationsfunktion $\rm (PAKF)$ der Walsh–Funktion $ \langle w_\nu^{(i)}\rangle$ wird mit $φ_{ii}(λ)$ bezeichnet, und es gilt:

$${\it \varphi}_{ii}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(i)} \right ] \hspace{0.05cm}.$$

Hinweise:

Die Aufgabe gehört zum Kapitel Spreizfolgen für CDMA.
Bezug genommen wird insbesondere auf den Abschnitt Walsh–Funktionen im Theorieteil.
Wir möchten Sie gerne auch auf das interaktive Applet Zur Erzeugung von Walsh-Funktionen hinweisen.
Die Abszisse ist auf die Chipdauer $T_c$ normiert. Das bedeutet, dass $λ = 1$ eigentlich eine Verschiebung um die Verzögerungszeit $τ = T_c$ beschreibt.

Fragebogen

Musterlösung

(1) Alle Vorschläge sind richtig:

Die Matrix $ {\mathbf{H}_{4}}$ ist die linke obere Teilmatrix von $ {\mathbf{H}_{8}}$.
Die Spreizfolgen ergeben sich aus den Zeilen 2, 3 und 4 von $ {\mathbf{H}_{4}}$, und stimmen mit den angegebenen Folgen überein.

(2) Richtig sind die Lösungsvorschläge 1, 2 und 3:

Entsprechend den Gleichungen im Angabenteil gilt:

$${\it \varphi}_{12}(\lambda = 0) = 1/4 \cdot \left [ (+1) \cdot (+1) + (-1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) \right ] = 0\hspace{0.05cm},$$

$${\it \varphi}_{13}(\lambda = 0) = 1/4\cdot \left [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm},$$

$${\it \varphi}_{23}(\lambda = 0) =1/4 \cdot \left [ (+1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm}.$$

Auch für größere Werte von $J$ ist für $i ≠ j$ der PKKF–Wert stets $φ_{ij}(λ = 0)= 0$.
Daraus folgt: Bei synchronem CDMA stören sich die Teilnehmer nicht.

(3) Richtig sind die Lösungsvorschläge 1 und 2:

Für alle Werte von $λ$ ist die PKKF $φ_{12}(λ) = 0$, wie die folgenden Zeilen zeigen:

$$\langle w_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$ $$\langle w_\nu^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_{\nu+1}^{(2)}\rangle = {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_{\nu+2}^{(2)}\rangle = {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_{\nu+3}^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle w_{\nu+4}^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} = \langle w_\nu^{(2)}\rangle \hspace{0.05cm}.$$

Verschiedene PKKF– und PAKF–Kurven

Das gleiche gilt für die PKKF $φ_{13}(λ)$.
Dagegen erhält man für die PKKF zwischen den Folgen $ \langle w_\nu^{(2)}\rangle$ und $ \langle w_\nu^{(3)}\rangle$:

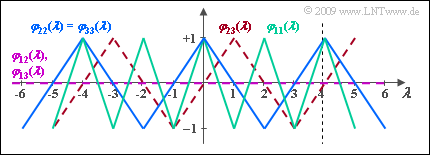
$${\it \varphi}_{23}(\lambda ) = \left\{ \begin{array}{c}0 \\+1\\ -1 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c} \lambda = 0, \pm 2, \pm 4,\pm 6, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -3, +1, +5, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -5, -1, +3, ... \hspace{0.05cm}. \\ \end{array}$$

Das bedeutet: Wird das Signal von Teilnehmer $3$ gegenüber Teilnehmer $2$ um ein Spreizchip verzögert oder umgekehrt, so lassen sich die Teilnehmer nicht mehr trennen und es kommt zu einer signifikanten Erhöhung der Fehlerwahrscheinlichkeit.
In der Grafik sind die PKKF–Kurven gestrichelt eingezeichnet (violett und rot).

(4) Richtig sind die Aussagen 1, 2 und 4:

Da die Walsh–Funktion Nr. $1$ periodisch ist mit $T_0 = 2T_c$, ist auch die PAKF periodisch mit $λ = 2$.
Die zweite Aussage ist richtig, wie die folgende Rechnung zeigt (grüner Kurvenzug):

$${\it \varphi}_{11}(\lambda = 0) = 1/4 \cdot \big [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (+1) + (-1) \cdot (-1) \big ] = +1\hspace{0.05cm},$$

$${\it \varphi}_{11}(\lambda = 1) = 1/4 \cdot \big [ (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) \big ] = -1\hspace{0.05cm}.$$

Da sich die beiden Walsh–Funktionen Nr. $2$ und $3$ nur durch eine Verschiebung um $T_c$ unterscheiden und sich eine Phase in der PAKF prinzipiell nicht auswirkt, ist tatsächlich entsprechend dem letzten Lösungsvorschlag $φ_{33}(λ) = φ_{22}(λ)$. Diese beiden PAKF–Funktionen sind blau eingezeichnet.
Dagegen unterscheidet sich $φ_{22}(λ)$ von $φ_{11}(λ)$ durch eine andere Periodizität: $φ_{22}(λ) = φ_{33}(λ)$ ist doppelt so breit wie $φ_{11}(λ)$.

	Für $J = 4$ ist $φ_{12}(λ = 0) = 0$.
	Für $J = 4$ ist $φ_{13}(λ = 0) = 0$.
	Für $J = 4$ ist $φ_{23}(λ = 0) = 0$.
	Für $J = 8$ kann durchaus $φ_{ij}(λ = 0) ≠ 0$ gelten $(i ≠ j)$.
	Bei synchronem CDMA stören sich die Teilnehmer nicht.

	Für alle Werte von $λ$ ist die PKKF $φ_{12}(λ) = 0$.
	Für alle Werte von $λ$ ist die PKKF $φ_{13}(λ) = 0$.
	Für alle Werte von $λ$ ist die PKKF $φ_{23}(λ) = 0$.
	Bei asynchronem CDMA stören sich die Teilnehmer nicht.

	Alle $φ_{ii}(λ)$–Kurven sind periodisch.
	Es gilt $φ_{11}(λ = 0) = +\hspace{-0.05cm}1$ und $φ_{11}(λ = 1) = -\hspace{-0.05cm}1$.
	Es gilt $φ_{22}(λ) = φ_{11}(λ)$.
	Es gilt $φ_{33}(λ) = φ_{22}(λ)$.

	$ \langle w_\nu^{(1)}\rangle = +\hspace{-0.05cm}1 -\hspace{-0.15cm}1 +\hspace{-0.15cm}1 -\hspace{-0.15cm}1$,
	$ \langle w_\nu^{(2)}\rangle = +\hspace{-0.05cm}1 +\hspace{-0.15cm}1 -\hspace{-0.15cm}1 -\hspace{-0.15cm}1$,
	$ \langle w_\nu^{(3)}\rangle = +\hspace{-0.05cm}1 -\hspace{-0.15cm}1 -\hspace{-0.15cm}1 +\hspace{-0.15cm}1$.